【BZOJ 2693】jzptab(莫比乌斯+分块)
2693: jzptab
Description
Input
一个正整数T表示数据组数
接下来T行 每行两个正整数 表示N、M
Output
T行 每行一个整数 表示第i组数据的结果
Sample Input
1
4 5Sample Output
122
HINT
T <= 10000
N, M<=10000000
【分析】
bzoj2154的进化版!多组。。
根据bzoj2154的推导我们有:
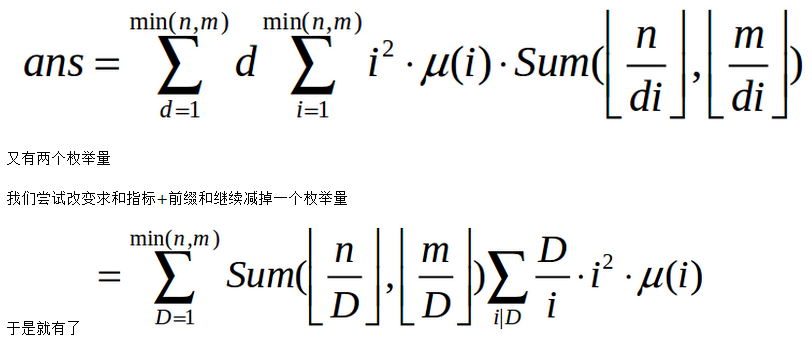
对于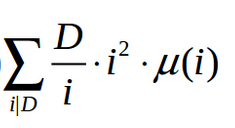 这个把它放入线性筛里面预处理就好了。
这个把它放入线性筛里面预处理就好了。
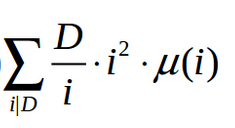 这个把它放入线性筛里面预处理就好了。
这个把它放入线性筛里面预处理就好了。 首先证明f[n]=∑i*mu[i](i|n)为积性函数:
设函数g[n]=n*mu[n],那么f=1*g,1和g都是积性函数,所以f也是积性函数。
线性筛的时候,当i%prime[j]!=0 由积性函数得,f[i*prime[j]]=f[i]*f[prime[j]]
当i%prime[j]==0时,若再加入prime[j],mu值为0,所以对答案没有影响。即f[i*prime[j]]=f[i]。
想这里的时候还是有思维局限,要记住当有一个质因子质数大于1时,mu值就为0了,这个特点前面一题也用到过!!
还有一个不是很懂的地方就是为什么每次加进去时都要MOD成正数,表示不知道化简之后为什么不能加一个负数进去~~导致WA很久~~
代码如下:

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 #include<cmath> 8 using namespace std; 9 #define Mod 100000009 10 #define Maxn 10000010 11 #define LL long long 12 13 LL mu[Maxn],pri[Maxn],g[Maxn],h[Maxn],pl; 14 bool q[Maxn]; 15 16 LL mymin(LL x,LL y) {return x<y?x:y;} 17 18 void get_mu(LL mx) 19 { 20 pl=0; 21 memset(q,1,sizeof(q)); 22 mu[1]=1;g[1]=1; 23 for(LL i=2;i<=mx;i++) 24 { 25 if(q[i]) 26 { 27 pri[++pl]=i; 28 mu[i]=-1; 29 g[i]=1+i*mu[i]; 30 } 31 for(LL j=1;j<=pl;j++) 32 { 33 if(i*pri[j]>mx) break; 34 q[i*pri[j]]=0; 35 if(i%pri[j]==0) mu[i*pri[j]]=0,g[i*pri[j]]=g[i]; 36 else mu[i*pri[j]]=-mu[i],g[i*pri[j]]=(g[i]*g[pri[j]])%Mod; 37 if(i%pri[j]==0) break; 38 } 39 } 40 for(LL i=1;i<=mx;i++) g[i]=(i*g[i])%Mod; 41 h[1]=g[1]; 42 for(LL i=2;i<=mx;i++) h[i]=(h[i-1]+g[i])%Mod; 43 } 44 45 LL get_sum(LL x,LL y) 46 { 47 return ( ( ((x+1)*x/2)%Mod )*( ((y+1)*y/2)%Mod ) )%Mod; 48 } 49 50 LL get_ans(LL n,LL m) 51 { 52 LL ans=0; 53 54 LL sq=(LL)ceil(sqrt((double)m)); 55 for(LL i=1;i<=mymin(sq,n);i++) 56 { 57 ans=(ans+(g[i]%Mod+Mod)%Mod*get_sum(n/i,m/i) )%Mod; 58 } 59 60 61 for(LL i=sq+1;i<=n;) 62 { 63 LL x=n/i,y=m/i; 64 LL r1=n/x+1,r2=m/y+1; 65 LL r=mymin(r1,r2); 66 if(r>m+1) r=m+1; 67 // if((((h[r-1]-h[i-1])%Mod+Mod)%Mod)<0) while(1); 68 ans=( ans+(((h[r-1]-h[i-1])%Mod+Mod)%Mod)*get_sum(x,y) )%Mod; 69 i=r; 70 } 71 return ans; 72 } 73 74 int main() 75 { 76 int T; 77 T=1; 78 scanf("%d",&T); 79 get_mu(10000000); 80 81 while(T--) 82 { 83 LL n,m,t; 84 scanf("%lld%lld",&n,&m); 85 if(n>m) t=n,n=m,m=t; 86 87 LL ans=get_ans(n,m); 88 89 printf("%lld\n",ans); 90 } 91 return 0; 92 }
2016-08-30 16:49:26


