【BZOJ 2820】 YY的GCD （莫比乌斯+分块）

YY的GCD
 

Description

神犇YY虐完数论后给傻×kAc出了一题
给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对
kAc这种傻×必然不会了，于是向你来请教……
多组输入

Input

第一行一个整数T 表述数据组数
接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2
10 10
100 100

Sample Output

30
2791

Hint

T = 10000

N, M <= 10000000

 

 

【分析】

　　

　　当Prime确定时，跟bzoj1101一样，得 ：
　　...=∑u[d]*(n/(Pri*d))*(m/(pri*d))     但是暴力枚举Pri应该很慢吧~~多组诶~~

　　然后通过前面几题我们知道u这里是可以快速求和的，而我们尽量让(n/(Pri*d))*(m/(pri*d) 这个部分是确定的，那么搞完u之后就可以直接√n分块了。

　　所以不妨设k=pri*d，把k变成我们要枚举的东西，原式= ∑u[k/Pri]*(n/k)*(m/k)  。

　　问题就变成求u[k/Pri]，它的意义是什么呢？相当于     - >

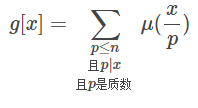                                                   这个东西~~

　　这个东西表示蒟蒻的脑子是想不出来怎么求的~~

 

　　直接放大神的解析：~~

　　

 

　　好像很有道理哦！！！！！

　　除了熟悉的积性函数，其他的我都不会线性筛了~~真是太年轻！！！

 

　　然后可爱的分块就可以了。

 

代码如下：

 1 #include<cstdio>
 2 #include<cstdlib>
 3 #include<cstring>
 4 #include<iostream>
 5 #include<algorithm>
 6 #include<queue>
 7 #include<cmath>
 8 using namespace std;
 9 #define Maxn 10000010
10 #define LL long long
11 
12 LL mu[Maxn],pri[Maxn],h[Maxn],g[Maxn],pl;
13 bool q[Maxn];
14 
15 LL mymin(LL x,LL y) {return x<y?x:y;}
16 
17 void get_mu(LL mx)
18 {
19     pl=0;
20     memset(q,1,sizeof(q));
21     mu[1]=1;g[1]=0;
22     for(LL i=2;i<=mx;i++)
23     {
24         if(q[i])
25         {
26             pri[++pl]=i;
27             mu[i]=-1;g[i]=1;
28         }
29         for(LL j=1;j<=pl;j++)
30         {
31             if(i*pri[j]>mx) break;
32             q[i*pri[j]]=0;
33             if(i%pri[j]==0) mu[i*pri[j]]=0,g[i*pri[j]]=mu[i];
34             else mu[i*pri[j]]=-mu[i],g[i*pri[j]]=mu[i]-g[i];
35             if(i%pri[j]==0) break;
36         }
37     }
38     h[1]=g[1];
39     for(int i=2;i<=mx;i++) h[i]=h[i-1]+g[i];
40 }
41 
42 int main()
43 {
44     freopen("a.in","r",stdin);
45     freopen("a.out","w",stdout);
46     get_mu(10000000);
47     int T;
48     scanf("%d",&T);
49     while(T--)
50     {
51         LL n,m,t;
52         scanf("%lld%lld",&n,&m);
53         if(n>m) t=n,n=m,m=t;
54         
55         LL ans=0;
56         
57         
58         LL sq=(LL)ceil(sqrt((double)m));
59         for(LL i=1;i<=mymin(sq,n);i++)
60         {
61             ans+=g[i]*(n/i)*(m/i);
62         }
63         
64         for(LL i=sq+1;i<=n;)
65         {
66             LL x=n/i,y=m/i;
67             LL r1=n/x+1,r2=m/y+1;
68             LL r=mymin(r1,r2);
69             if(r>m+1) r=m+1;
70             ans+=(h[r-1]-h[i-1])*x*y;
71             i=r;
72         }
73         
74         printf("%lld\n",ans);
75         
76     }
77     return 0;
78 }
[BZOJ2820]

 

2016-08-30 11:45:40

 

posted @ 2016-08-30 11:42  konjak魔芋  阅读(160)  评论(0)  编辑  收藏  举报