【转】【最大子矩阵问题】【悬线法】 学习笔记
学习材料：王知昆《浅谈用极大化思想解决最大子矩阵问题》
【最大子矩阵问题】
在一个给定的矩形中有一些障碍点，找出内部不包含障碍点的、轮廓与整个矩形平行或重合的最大子矩形。
【定义子矩形】
有效子矩形：内部不包含障碍点的、轮廓与整个矩形平行或重合的子矩形。
极大子矩形：每条边都不能向外扩展的有效子矩形。
最大子矩形：所有有效子矩形中最大的一个（或多个）。
【极大化思想】
在一个有障碍点的矩形中最大子矩形一定是极大子矩形。
设计算法的思路：枚举所有的极大子矩形，找到最大子矩形。
设NM分别为整个矩形的长和宽，S为内部的障碍点数。
【算法1】
时间复杂度：O（S^2） 空间复杂度：O（S）
由于极大子矩形的每一条边都不能向外扩展，那么极大子矩阵的每条边要么覆盖了障碍点，要么与整个矩形的边界重合
基本算法：枚举上下左右四个边界，然后判断组成的矩形是否是有效子矩形。
复杂度：O（S^5） 可以改进的地方：产生了大量的无效子矩形。
初步改进的算法：枚举左右边界，然后对处在边界内的点排序，每两个相邻的点和左右边界组成一个矩形。
复杂度：O（S^3） 可以改进的地方：枚举了部分不是极大子矩形的情况。
综上，设计算法的方向：
1、保证每一个枚举的矩形都是有效的。
2、保证每一个枚举的矩形都是极大的。
算法的过程：
枚举极大子矩形的左边界——>根据确定的左边界，找出相关的极大子矩形——>检查和处理遗漏的情况
(1)按照横坐标从小到大的顺序将所有的点编号为1，2，3...
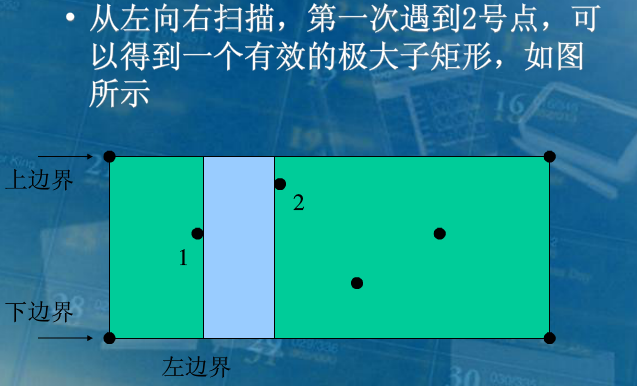
(2)首先选取1号点作为要枚举的极大子矩形的左边界，设定上下边界为矩形的上下边界
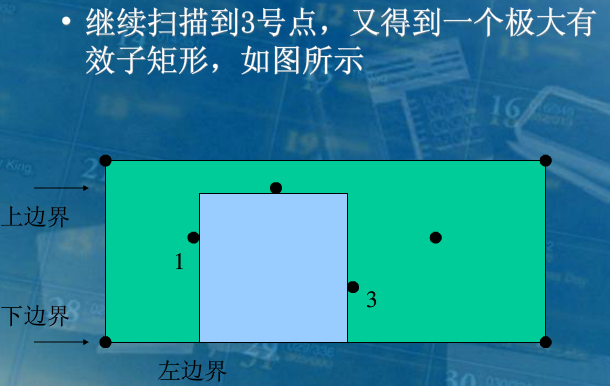
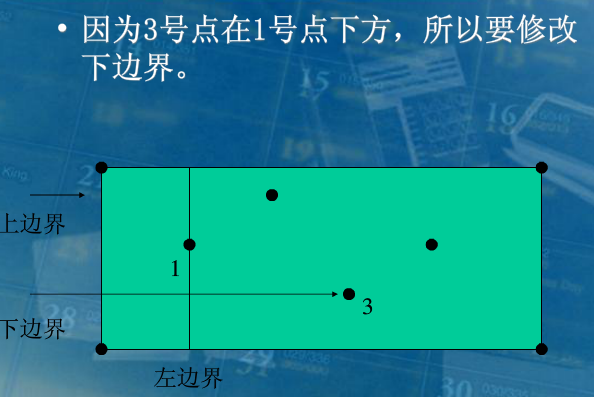
(3)从左到右扫描，第一次到2号点，确定一个极大子矩形，修改上下边界；第二次找到3号点，以此类推。
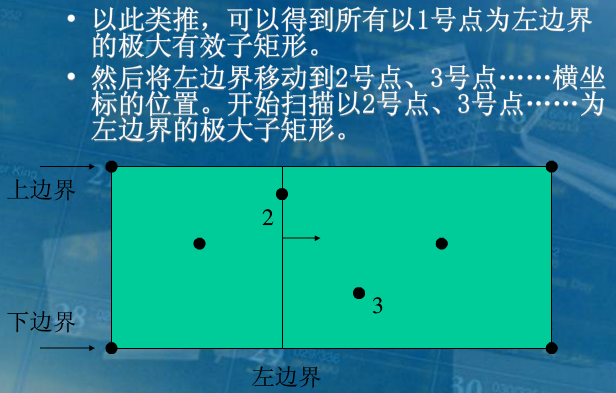
(4)将左边界移动到2号点，3号点，，，以同样的方法枚举
遗漏的情况：
1、矩形的左边界与整个矩形的左边界重合。解决方法：用类似的方法从左到右扫一遍
2、矩形的左边界与整个矩形的左边界重合，且矩形的右边界与整个矩形的右边界重合。解决方法：预处理时增加特殊判断。
优点：利用的极大化思想，复杂度可以接受，编程实现简单。
缺点：使用有一定的局限性，不适合障碍点较密集的情况。
【算法2】
时间复杂度O(NM) 空间复杂度O(NM)
定义
有效竖线：除了两个端点外，不覆盖任何一个障碍点的竖直线段。
悬线：上端覆盖了一个障碍点或者到达整个矩形上边界的有效线段。
每个悬线都与它底部的点一一对应，矩形中的每一个点（矩形顶部的点除外）都对应了一个悬线。
悬线的个数=(N-1)*M；
如果把一个极大子矩形按照横坐标的不同切割成多个与y轴平行的线段，那么其中至少有一个悬线。
如果把一个悬线向左右两个方向尽可能的移动，那么就得到了一个矩形，我们称它为悬线对应的矩形。
悬线对应的矩形不一定是极大子矩形，因为下边界可能还可以向下扩展。
设计算法：
具体方法：
代码实现具体见WC2002 奶牛浴场（算法1）
codevs1159最大全0子矩阵（算法2）
补图：
算法1：
s为障碍点总数。
枚举一个障碍点作为左边界O（s），然后不断向后扫得到极大子矩形O（s），总复杂度为O（s^2）。
当1障碍点数较小时，可以使用算法1。
算法2（悬线法）：
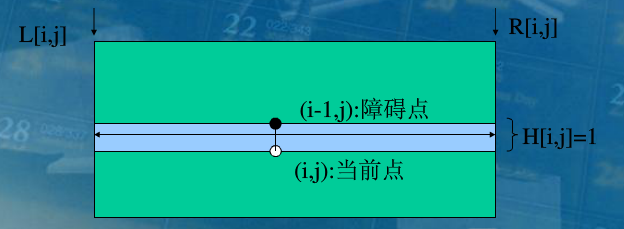
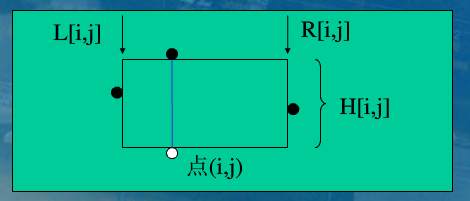
当障碍点较多，n*m较小时，可以用悬线法。
时间复杂度为O（n*m）。
例题：bzoj1057
猴似猴塞雷~~
2016-08-19 15:02:38
