[NOI2016] 优秀的拆分 题解

[NOI2016] 优秀的拆分 题解

link

题意

\(T\) 组询问，每组一个字符串 \(s\)

求 \(s\) 所有字串分成 \(AABB\) 的方案数之和。 \(A,B\) 为非空串。

题解

设 \(f_i\) 为一 \(i\) 结尾的 \(AA\) 串数量，\(g_i\) 为一 \(i\) 结尾的 \(AA\) 穿数量。

\(ans=\sum f_{i}\times g_{i+1}\)

考虑求 \(f,g\) ，用后缀数组。需要多反转后建一个，用于求 \(\text{lcs}\)

枚举 \(A\) 的长度 \(w\) ，之后所有相隔 \(w\) 的小标是对应的。

在 \(w\) 倍数处设置关键点，则一个 \(A\) 最少经过一个关键点。

枚举相邻的关键点 \(l,r\) ，求 \(lcp=\text{lcp}(l,r),lcs=\text{lcs}(l,r)\)

则 \(lcp+lcs\) 为经过两个关键点且开头距离为 \(w\) 的最长公共子串。

如果 \(lcp+lcs\ge w\) 则存在合法的 \(AA\) 串，相当于一个区间加，用差分搞一下

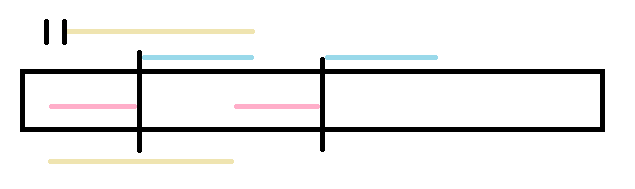
如图，黑色部分任意一个位置为起点都可以形成 \(AA\) 串，结尾同理

最终复杂度为一个调和级数，就是 \(O(n\log n)\)

代码

#include <bits/stdc++.h>
#define clr(x) memset(x, 0, sizeof(x))
using namespace std;
const int N = 30005;
char a[N];
int n, lg[N];
long long ff[N], gg[N];
struct suf {
	int sa[N], rk[N], old[N], t[N], id[N], m, h[N], f[N][17];
	inline void rs() {
	    for (int i = 1; i <= m; i++) t[i] = 0;
	    for (int i = 1; i <= n; i++) ++t[rk[i]];
	    for (int i = 1; i <= m; i++) t[i] += t[i - 1];
	    for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
	}
	inline int EQ(int x, int y, int k)
	{ return old[x] == old[y] && old[x + k] == old[y + k]; }
	inline void bui() {
		clr(sa), clr(rk), clr(old), clr(t), clr(id), clr(h);
		memset(f, 10, sizeof(f));
	    m = 200;
	    for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
	    rs();
	    for (int k = 1, p; k <= n; k <<= 1) {
	        p = 0;
	        for (int i = n - k + 1; i <= n; i++) id[++p] = i;
	        for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
	        rs(), memcpy(old, rk, sizeof(rk)), p = 0;
	        for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
	        if (p == n) break;
	        m = p;
	    }
	    for (int i = 1, j, k = 0; i <= n; h[rk[i++]] = k)
        	for (k ? --k : 0, j = sa[rk[i] - 1]; a[i + k] == a[j + k]; k++);
        for (int i = 1; i <= n; i++) f[i][0] = h[i];
        for (int j = 1; j <= 15; j++)
        	for (int i = 1; i + (1 << j - 1) <= n; i++)
        		f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
	}
	inline int lcp(int x, int y) {
		x = rk[x], y = rk[y];
		if (x == y) return n - sa[x] + 1;
		if (x > y) x ^= y ^= x ^= y; x++;
		int k = lg[y - x + 1];
		return min(f[x][k], f[y - (1 << k) + 1][k]);
	}
};
suf A, B;
inline void sol() {
	memset(ff, 0, sizeof(ff));
	memset(gg, 0, sizeof(gg));
	A.bui();
	reverse(a + 1, a + n + 1);
	B.bui();
	for (int w = 1; w <= n / 2; w++)
		for (int l = w, r; l + w <= n; l += w) {
			r = l + w;
			int lcp = min(w, A.lcp(l, r));
			int lcs = min(w - 1, B.lcp(n - l + 2, n - r + 2));
			if (lcp + lcs >= w) {
				int t = lcp + lcs - w + 1;
				ff[r + lcp - t]++, ff[r + lcp]--;
				gg[l - lcs]++, gg[l - lcs + t]--;
			}
		}
	for (int i = 1; i <= n; i++) ff[i] += ff[i - 1], gg[i] += gg[i - 1];
	long long ans = 0;
	for (int i = 1; i < n; i++) ans += ff[i] * gg[i + 1];
	printf("%lld\n", ans);
}
int main() {
	for (int i = 2; i <= 30000; i++) lg[i] = lg[i >> 1] + 1;
	int Ti;
	scanf("%d", &Ti);
	while (Ti--) {
		scanf("%s", a + 1);
		n = strlen(a + 1);
		sol();
	}	
}