向量初步
向量初步
做凸包和一些 USACO 的题要用
Start
-
既有大小,又有方向的量,如速度
-
表示方法:字母上加箭头 \(\overrightarrow{a}\)
-
若向量起点为 \(A\) 终点为 \(B\) 向量可表示为 \(\overrightarrow{AB}\)
-
向量的大小:表示为 \(|\overrightarrow{a}|\) 或 \(|\overrightarrow{AB}|\)
-
零向量:\(\overrightarrow{O},|\overrightarrow{O}|=O\),起点和终点重合,方向任意
-
单位向量:长度为一个单位的向量
-
在平面直角坐标系中,将向量 \(\overrightarrow{a}\) 平移,使起点和原点重合,终点位于点 \((x,y)\) ,
则实数对 \((x,y)\) 为向量 \(\overrightarrow{a}\) 的坐标,记为 \(\overrightarrow{a}=(x,y)\) 。
-
加法:\(\overrightarrow{A}+\overrightarrow{B}=(x_1+x_2,y_1+y_2)\)
-
向量加法满足交换律和结合律
-
减法 \(\overrightarrow{A}-\overrightarrow{B}=(x_1-x_2,y_1-y_2)\)
-
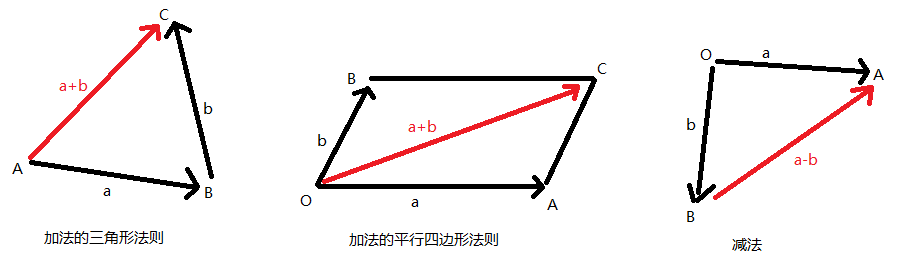
-
已知 \(A(x_1,y_1),B(x_2,y_2)\),则\(\overrightarrow{AB}=B-A\)
点积
-
点积就是 \(a\cdot b=x_1x_2+y_1y_2\)
-
几何意义:两个向量的起点共点时的夹角,以及 \(b\) 在 \(a\) 方向上的投影。
\(a\cdot b=|a||b|\cos\theta\) ,其中 \(\theta\) 为夹角
-
点积有以下性质
- \(a\cdot b=0\),则 \(a\perp b\)
- \(a\cdot b<0\),则夹角 \(>90^\circ\)
- \(a\cdot b>0\),则夹角 \(<90^\circ\)
- 自乘,\(|a|^2=a\cdot a\)
- 交换律和结合律
叉积
-
叉积就是 \(a\times b=\det \left [ \begin{array}{} x_1 & x_2 \\ y_1 & y_2 \end{array}\right ]=x_1y_2-x_2y_1\)
-
几何意义:两个向量的起点共点时,所形成的平行四边形面积
-
性质
-
\(a\times b=0\),a 和 b 共线,方向相同或相反
-
\(a\times b>0\),a 在 b 顺时针方向
-
\(a\times b<0\),a 在 b 逆时针方向
向量旋转
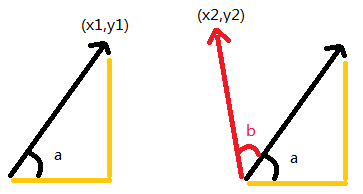
如图,将向量 \(R\) 逆时针旋转 \(\beta\)
\(x_1=|R|\cos \alpha\)
\(y_1=|R|\sin \alpha\)
\(x_2=|R|\cos {\alpha+\beta}\)
\(y_2=|R|\sin {\alpha+\beta}\)
于是展开 \(\cos {\alpha+\beta}\) 和 \(\sin {\alpha+\beta}\)
\(x_2=|R|(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\)
\(y_2=|R|(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\)
将 \(\sin \alpha=\dfrac{y_1}{|R|}\) 和 \(\cos \alpha=\dfrac{x_1}{|R|}\) 带入得
\(x_2=|R|(\dfrac{x_1}{|R|}\cos\beta-\dfrac{y_1}{|R|}\sin\beta)=x_1\cos\beta-y_1\sin\beta\)
\(y_2=|R|(\dfrac{y_1}{|R|}\cos\beta+\dfrac{x_1}{|R|}\sin\beta)=x_1\sin\beta+y_1\cos\beta\)
顺时针旋转吧角度该成负数即可
\(x_2=x_1\cos(-\beta)-y_1\sin(-\beta)=x_1\cos\beta+y_1\sin\beta\)
\(y_2=x_1\sin(-\beta)+y_1\cos(-\beta)=-x_1\sin\beta+y_1\cos\beta\)
任意角
角可以看成平面内一条射线绕其端点从一个位置旋转到另一个位置形成的图形。
开始的位置称为始边,结束的位置称为终边
按逆时针旋转的角叫做正角,顺时针旋转的角叫做负角,没有旋转的角叫做零角。
于是角被推广到了任意角
弧度制
我们以前都用角度制,而现在角被推广到了任意角,角度值无法满足一些要求
于是有了弧度制,一弧度用 \(\text{rad}\) 表示,读作:弧度
一般地,正角的弧度数为正,负角的弧度数为负,零角的弧度数为 0
若半径 \(r\) 的圆心角 \(\alpha\) 弧长为 \(l\) ,发现 \(l=\dfrac{\alpha\pi r}{180}\),可以发现 \(\alpha\) 只与 \(\dfrac{l}{r}\) 有关
所以:长度等于半径的长的弧所对圆心角叫做一弧度的角

