KMP 算法
KMP
给一个待匹配的文本串和一个需要在文本中搜索的模式串,在文本串中,模式串出现的次数、位置等
-
朴素算法:枚举每个文本串元素,从这一位开始比较,每次失败就从头开始比对,
很容易可以把这个算法卡成 \(O(nm)\)
-
KMP 算法思想:每次失败,不会从头开始枚举,而是从某个特定位置开始
模式串的每一位都有固定的变化值,每次失配后不用从头匹配,从而节省时间。比如
模式串:abcabc 文本串:abcabdababcabc第六位失配了,直接将模式串移动到文本串的第 4 位
模式串: abcabc 文本串:abcabdababcabc -
移位法则:在模式串 s 中,对于一个 \(s_i\) 应该记录跳转位置 \(nxt_i=j\) 使得 \(j<i,s_i=s_j\)
且对于 \(j\ne1\) 有 \(s_1\) ~ \(s_{j-1}\)\(=s_{i-j+1}\) ~ \(s_{i-1}\) 按位相等
其实就是用 \(nxt\) 数组记录模式串到 \(i\) 为止真前缀和真后缀最大相同位置
实现
匹配部分
比较简单
for(int i=0,j=0;i<=n;i++) {
while(j && x[i]!=y[j+1])j=nxt[j];
if(x[i]==y[j+1])++j;
if(j==m) {
printf("%d\n",i-m+1);
j=nxt[j];
}
}
求 nxt 数组部分
考虑自己匹配自己
for(int i=2,j=0;i<=m;i++) {
while(j && y[i]!=y[j+1])j=nxt[j];
if(y[i]==y[j+1])++j;
nxt[i]=j;
}
-
每次最多向后匹配一位 nxt
-
j 用于比对前后缀,对于一对前后缀而言,第 i-1 和 j-1 位前都有异同,
这决定 i 与 j 的匹配结果从哪开始
Code
#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
int n,m,nxt[N];
char x[N],y[N];
int main() {
scanf("%s%s",x+1,y+1);
n=strlen(x+1),m=strlen(y+1);
for(int i=2,j=0;i<=m;i++) {
while(j && y[i]!=y[j+1])j=nxt[j];
if(y[i]==y[j+1])++j;
nxt[i]=j;
}
for(int i=0,j=0;i<=n;i++) {
while(j && x[i]!=y[j+1])j=nxt[j];
if(x[i]==y[j+1])++j;
if(j==m) {
printf("%d\n",i-m+1);
j=nxt[j];
}
}
for(int i=1;i<=m;i++)printf("%d ",nxt[i]);
}
时间复杂度
对于每一个 i ,j 至多增加 m 次,所以至多减少 m 次,为 \(O(n+m)\)
ex KMP
扩展 \(\text{KMP}\) 算法,求模式串的每一个后缀与文本串的最大公共前缀,在 \(O(n+m)\) 的时间内
分两部分求解
此处假设 \(S\) 为文本串,\(T\) 为模式串
z 函数
\(z_i\) 表示 \(T\) 以 \(i\) 开头的后缀与 \(T\) 自己的最大公共前缀。
假设当前 \(z_{1,2,\cdots,x-1}\) 已经求出,考虑求 \(z_x\)
做法:对于 \(i<x\) ,记录 \(i+z_i-1\) 的最大值 \(r\) 以及 \(l\) 为其对应的 \(i\)
由 \(z\) 的定义可得 \([l,r]\) 和 \([1,z_l]\) 对应相等

-
\(x\le r\)
在 \([l,r]\) 中找到 \(x\) 的对应位置,可得蓝色段相等

由 \(z_{x-l+1}\) 的定义,可得红色部分相等

- \(i+z_{x-l+1}\le r\) ,\(z_x=z_{x-l+1}\)
- \(i+z_{x-l+1}>r\) ,则我们只知道 \(z_x\) 至少为 \(r-x+1\) ,剩下的暴力向后扩展
-
\(x>r\) 啥都不知道,直接扩展
实现:
int z[N];
char b[N];
z[1] = m;
for (int i = 2, l = 0, r = 0; i <= m; i++) {
if (i <= r) z[i] = min(z[i - l + 1], r - i + 1);
while (i + z[i] <= m && b[i + z[i]] == b[z[i] + 1]) ++z[i];
if (i + z[i] - 1 > r) r = i + z[i] - 1, l = i;
}
无论是思路、实现还是复杂度分析,都很像 manacher 算法。
复杂度显然 \(O(n)\)
ex 数组
\(ex_i\) 就是 \(T\) 以 \(i\) 开头的后缀与 \(S\) 的最大公共前缀
原理类似 \(z\) 函数,记录 \(i+ex_i-1\) 最大值 \(r\) 以及对应 \(l\)
放个图吧
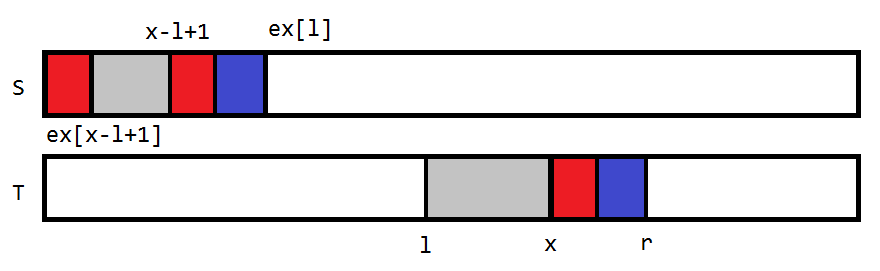
依然可以分类讨论 + 暴力扩展完成 \(O(n)\) 解决
char a[N];
int ex[N];
for (int i = 1, l = 0, r = 0; i <= n; i++) {
if (i <= r) ex[i] = min(z[i - l + 1], r - i + 1);
while (i + ex[i] <= n && a[i + ex[i]] == b[ex[i] + 1]) ++ex[i];
if (i + ex[i] - 1 > r) r = i + ex[i] - 1, l = i;
}
例题
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 2e7 + 5;
int n, m, z[N], ex[N];
LL ans;
char C, a[N], b[N];
int main() {
C = getchar();
for (; C < 'a' || C > 'z'; C = getchar());
for (; C > '`' && C < '{'; C = getchar()) a[++n] = C;
C = getchar();
for (; C < 'a' || C > 'z'; C = getchar());
for (; C > '`' && C < '{'; C = getchar()) b[++m] = C;
z[1] = m;
for (int i = 2, l = 0, r = 0; i <= m; i++) {
if (i <= r) z[i] = min(z[i - l + 1], r - i + 1);
while (i + z[i] <= m && b[i + z[i]] == b[z[i] + 1]) ++z[i];
if (i + z[i] - 1 > r) r = i + z[i] - 1, l = i;
}
ans = 0;
for (int i = 1; i <= m; i++) ans ^= 1ll * i * (z[i] + 1);
printf("%lld\n", ans);
for (int i = 1, l = 0, r = 0; i <= n; i++) {
if (i <= r) ex[i] = min(z[i - l + 1], r - i + 1);
while (i + ex[i] <= n && a[i + ex[i]] == b[ex[i] + 1]) ++ex[i];
if (i + ex[i] - 1 > r) r = i + ex[i] - 1, l = i;
}
ans = 0;
for (int i = 1; i <= n; i++) ans ^= 1ll * i * (ex[i] + 1);
printf("%lld\n", ans);
}

