【20151105noip膜你赛】bzoj3652 bzoj3653
题目仿佛在讽刺我。。。

第一题:
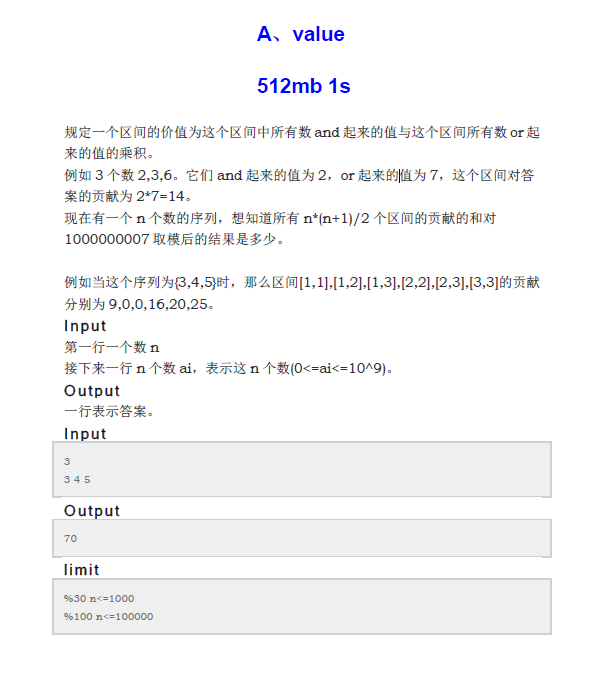
题解:
考虑枚举区间右端点,维护所以左到当前的 and 和 or 。注意 and 每次变化至少有一个二进制位从1变 0,or 每次至少有一个位从0变 1,所以最多有log段不同的值。用两个链表维护这log个值,暴力计算答案即可。
O( nlogn)
我原本打的是一个树状数组的O(nlognlogn)算法。。然后被卡了。。只有50分。。
看了看奥爷爷的代码,发现他直接用一个链表同时维护and和or值,真奇怪啊不是(logn)^2吗。。然后男神说这个也是log级别的,因为两个区间不同只能是边界上跨越。
代码:
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<algorithm>
6 using namespace std;
7
8 typedef long long LL;
9 const int N=100010;
10 const LL mod=1000000007;
11 int n,al;
12 struct node{int last,next;LL t0,t1,sum;}a[N];
13
14 int main()
15 {
16 // freopen("a.in","r",stdin);
17 // freopen("a.out","w",stdout);
18 freopen("value.in","r",stdin);
19 freopen("value.out","w",stdout);
20 scanf("%d",&n);
21 al=0;
22 int x,last=0;
23 LL ans=0;
24 for(int i=1;i<=n;i++)
25 {
26 scanf("%d",&x);
27 for(int j=last;j;j=a[j].last)
28 {
29 a[j].t0&=x;
30 a[j].t1|=x;
31 }
32 a[++al].t0=x;a[al].t1=x;a[al].sum=1;
33 a[al].last=last;
34 if(last) a[last].next=al;
35 last=al;
36
37 for(int j=last;j;j=a[j].last)
38 {
39 int p=a[j].last;
40 if(p && a[p].t0==a[j].t0 && a[p].t1==a[j].t1)
41 {
42 a[p].sum+=a[j].sum;
43 a[p].next=a[j].next;
44 if(a[j].next) a[a[j].next].last=p;
45 else last=p;//debug last=p not last=j
46 }
47 }
48
49 for(int j=last;j;j=a[j].last)
50 {
51 ans=(ans+((((a[j].t0*a[j].t1)%mod)*a[j].sum)%mod))%mod;
52 }
53 }
54 printf("%I64d\n",ans);
55 return 0;
56 }
第二题 bzoj3652
3652: 大新闻
Time Limit: 10 Sec Memory Limit: 512 MBSec Special JudgeSubmit: 207 Solved: 106
[Submit][Status][Discuss]
Description

Input 两个整数n和p。p/100表示题目中描述的概率
Output 输出期望在模1000000007下的值
Sample Input
3 50
Sample Output
2
HINT

1<=N<=10^18

1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<algorithm>
6 using namespace std;
7
8 typedef long long LL;
9 const LL mod=1000000007;
10 const int N=100;
11 LL n,m,p,bit[N],vis[N][2][2],cnt[N][2],f[N][2][2][2][2],g[N][2][2];
12 int d[N];
13
14 LL ad(LL x,LL y){return ((x+y)%mod+mod)%mod;}
15
16 int find_vis(int x,int now,int flag)
17 {
18 if(x==0) return 1;
19 if(vis[x][now][flag]!=-1) return vis[x][now][flag];
20 int mx=1;if(flag || (x-1==0)) mx=d[x-1];
21 LL ans=0;
22 for(int i=0;i<=mx;i++)
23 {
24 ans=ad(ans,find_vis(x-1,i,flag&(i==d[x-1])));
25 }
26 vis[x][now][flag]=ans;
27 // printf("x = %d now = %d flag = %d = %d\n",x,now,flag,ans);
28 return ans;
29 }
30
31 void find_cnt()
32 {
33 for(int i=1;i<=m;i++) cnt[i][0]=cnt[i][1]=bit[m];
34 for(int i=m;i>=1;i--)
35 {
36 if(d[i]==0)
37 {
38 for(int j=i-1;j>=1;j--)
39 {
40 cnt[j][0]=ad(cnt[j][0],-bit[i-1]);
41 cnt[j][1]=ad(cnt[j][1],-bit[i-1]);
42 }
43 cnt[i][1]=ad(cnt[i][1],-bit[i]);
44 for(int j=i+1;j<=m;j++)
45 {
46 cnt[j][d[j]]=ad(cnt[j][d[j]],-bit[i]);
47 }
48 }
49 }
50
51 }
52
53 int dfs(int x,int now1,int now2,int flag1,int flag2)
54 {
55 if(x==0) return 0;
56
57 if(f[x][now1][now2][flag1][flag2]!=-1) return f[x][now1][now2][flag1][flag2];
58 LL ans=0,now=0;
59 int mx1=1;if(flag1 || (x-1==0)) mx1=d[x-1];
60 int mx2=1;if(flag2 || (x-1==0)) mx2=d[x-1];
61 if(now1+now2==1) ans=ad(ans,(vis[x][now1][flag1]*bit[x])%mod);
62 for(int i=0;i<=mx1;i++)
63 {
64 if(flag2 && (i^1)>mx2)
65 {
66 int f1=flag1&(i==d[x-1]);
67 int f2=flag2&(0==d[x-1]);
68 ans=ad(ans,dfs(x-1,i,0,f1,f2));
69 }
70 else
71 {
72 int f1=flag1&(i==d[x-1]);
73 int f2=flag2&((i^1)==d[x-1]);
74 ans=ad(ans,dfs(x-1,i,i^1,f1,f2));
75 }
76 }
77 f[x][now1][now2][flag1][flag2]=ans;
78 // printf("f x = %d now1 = %d now2 = %d flag1 = %d flag2 = %d ans = %d\n",x,now1,now2,flag1,flag2,ans);
79 return ans;
80 }
81
82 int DFS(int x,int now,int flag)
83 {
84 if(x==0) return 0;
85 if(g[x][now][flag]!=-1) return g[x][now][flag];
86 int mx=1;if(flag || (x-1==0)) mx=d[x-1];
87 LL ans=0;
88 ans=ad(ans,(((vis[x][now][flag]*cnt[x][now^1])%mod)*bit[x])%mod);
89 for(int i=0;i<=mx;i++)
90 {
91 ans=ad(ans,DFS(x-1,i,flag&(i==d[x-1])));
92 }
93 g[x][now][flag]=ans;
94 // printf("g x = %d now = %d flag = %d = %d\n",x,now,flag,ans);
95 return ans;
96 }
97
98 LL quickpow(LL x,LL y)
99 {
100 LL ans=1;
101 while(y)
102 {
103 if(y&1) ans=(ans*x)%mod;
104 x=(x*x)%mod;
105 y/=2;
106 }
107 return ans;
108 }
109
110 int main()
111 {
112 freopen("a.in","r",stdin);
113 // freopen("a.out","w",stdout);
114 // freopen("news.in","r",stdin);
115 // freopen("news.out","w",stdout);
116 scanf("%lld%lld",&n,&p);
117 LL x=n-1;m=0;
118 memset(d,0,sizeof(d));
119 while(x)
120 {
121 d[++m]=x%2;
122 x/=2;
123 }
124 bit[1]=1;
125 for(int i=2;i<=70;i++) bit[i]=(bit[i-1]*2)%mod;
126 memset(cnt,0,sizeof(cnt));
127 memset(vis,-1,sizeof(vis));
128 memset(f,-1,sizeof(f));
129 memset(g,-1,sizeof(g));
130 find_vis(m+1,0,1);
131 find_cnt();
132
133 LL a1=dfs(m+1,0,0,1,1);
134 LL a2=DFS(m+1,0,1);
135 LL bn=quickpow(n%mod,mod-2);
136 LL bb=quickpow(100,mod-2);
137 LL ans=0;
138
139 // for(int i=1;i<=3;i++)
140 // for(int j=0;j<=1;j++)
141 // printf("cnt %d %d = %I64d\n",i,j,cnt[i][j]);
142
143 ans=ad(ans,(((a1*bn)%mod)*((p*bb)%mod))%mod);
144 ans=ad(ans,(((((a2*bn)%mod)*bn)%mod)*(((100-p)*bb)%mod))%mod);
145 // printf("a1=%I64d a2=%I64d\n",a1,a2);
146 printf("%lld\n",ans);
147 return 0;
148 }
x表示当前填到哪一位。flag表示当前是否和边界重合。
dfs是做加密的情况,也就是确定当前填的x,然后让跟它异或的y尽量大。
DFS是做不加密的情况,也就是确定当前填的x,然后y所有可能都算上。
其中vis是维护到当前状态的方案数。
cnt是表示当前某个数位上是0或1的方案数。
好了还是这种做法太复杂了。。
学习了一下出题人的做法。
出题人题解:

1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cmath>
5 #include<iostream>
6 #include<algorithm>
7 using namespace std;
8
9 typedef long long LL;
10 const LL mod=1000000007;
11 const int N=110;
12 LL n,m,p,bit[N],f[N][2][2],g[N][2][2];
13 int a[N];
14
15 LL quickpow(LL x,LL y)
16 {
17 LL ans=1;
18 while(y)
19 {
20 if(y&1) ans=(ans*x)%mod;
21 x=(x*x)%mod;
22 y/=2;
23 }
24 return ans;
25 }
26
27 void dp_1()
28 {
29 memset(f,0,sizeof(f));
30 memset(g,0,sizeof(g));
31 g[0][1][1]=1;
32 int now1,now2;
33 for(int i=0;i<m;i++)
34 for(int x1=0;x1<=1;x1++)
35 for(int x2=0;x2<=1;x2++)
36 {
37 if(g[i][x1][x2]==0) continue;
38 for(int j=0;j<=1;j++)
39 {
40 int k=j^1;
41 if(j>a[i+1] && x1) continue;
42 if(j==a[i+1] && x1) now1=1;
43 else now1=0;
44 if(k>a[i+1] && x2) k=0;
45 if(k==a[i+1] && x2) now2=1;
46 else now2=0;
47 g[i+1][now1][now2]=(g[i+1][now1][now2]+g[i][x1][x2])%mod;
48 f[i+1][now1][now2]=(f[i+1][now1][now2]+f[i][x1][x2]+((g[i][x1][x2]*(j^k))%mod*bit[i+1])%mod)%mod;
49 }
50 }
51 }
52
53
54 void dp_2()
55 {
56 memset(f,0,sizeof(f));
57 memset(g,0,sizeof(g));
58 g[0][1][1]=1;
59 int now1,now2;
60 for(int i=0;i<m;i++)
61 for(int x1=0;x1<=1;x1++)
62 for(int x2=0;x2<=1;x2++)
63 {
64 if(g[i][x1][x2]==0) continue;
65 for(int j=0;j<=1;j++)
66 {
67 if(j>a[i+1] && x1) continue;
68 if(x1 && j==a[i+1]) now1=1;
69 else now1=0;
70 for(int k=0;k<=1;k++)
71 {
72 if(k>a[i+1] && x2) continue;
73 if(x2 && k==a[i+1]) now2=1;
74 else now2=0;
75 g[i+1][now1][now2]=(g[i+1][now1][now2]+g[i][x1][x2])%mod;
76 f[i+1][now1][now2]=(f[i+1][now1][now2]+f[i][x1][x2]+(g[i][x1][x2]*(j^k))%mod*bit[i+1]%mod)%mod;
77 }
78 }
79 }
80 }
81
82
83 int main()
84 {
85 freopen("a.in","r",stdin);
86 // freopen("news.in","r",stdin);
87 // freopen("news.out","w",stdout);
88 scanf("%lld%lld",&n,&p);
89 LL x=n-1,a1=0,a2=0;m=0;
90 while(x)
91 {
92 a[++m]=x%2;
93 x/=2;
94 }
95 for(int i=1;i<=m/2;i++) swap(a[i],a[m-i+1]);
96 bit[m]=1;
97 for(int i=m-1;i>=1;i--) bit[i]=(bit[i+1]*2)%mod;
98 // for(int i=1;i<=m;i++) printf("%d ",a[i]);printf("\n");
99
100 dp_1();
101 for(int i=0;i<=1;i++)
102 for(int j=0;j<=1;j++)
103 a1=(a1+f[m][i][j])%mod;
104 dp_2();
105 for(int i=0;i<=1;i++)
106 for(int j=0;j<=1;j++)
107 a2=(a2+f[m][i][j])%mod;
108
109 LL bn=quickpow(n%mod,mod-2);
110 LL bb=quickpow(100,mod-2);
111 LL ans=0;
112
113 ans=(ans+((a1*bn%mod)*(p*bb%mod))%mod)%mod;
114 ans=(ans+((((a2*bn%mod)*bn)%mod)*((100-p)*bb%mod))%mod)%mod;
115 // printf("a1=%I64d a2=%I64d\n",a1,a2);
116 printf("%lld\n",ans);
117
118 return 0;
119 }
第三题:
3653: 谈笑风生
Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 689 Solved: 264
[Submit][Status][Discuss]
Description
设T 为一棵有根树,我们做如下的定义:
• 设a和b为T 中的两个不同节点。如果a是b的祖先,那么称“a比b不知道
高明到哪里去了”。
• 设a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定
常数x,那么称“a 与b 谈笑风生”。
给定一棵n个节点的有根树T,节点的编号为1 到 n,根节点为1号节点。你需
要回答q 个询问,询问给定两个整数p和k,问有多少个有序三元组(a;b;c)满足:
1. a、b和 c为 T 中三个不同的点,且 a为p 号节点;
2. a和b 都比 c不知道高明到哪里去了;
3. a和b 谈笑风生。这里谈笑风生中的常数为给定的 k。
Input
输入文件的第一行含有两个正整数n和q,分别代表有根树的点数与询问的个数。接下来n - 1行,每行描述一条树上的边。每行含有两个整数u和v,代表在节点u和v之间有一条边。
接下来q行,每行描述一个操作。第i行含有两个整数,分别表示第i个询问的p和k。
Output
输出 q 行,每行对应一个询问,代表询问的答案。
Sample Input
1 2
1 3
2 4
4 5
2 2
4 1
2 3
Sample Output
3
1
3
HINT
1<=P<=N
1<=K<=N
N<=300000
Q<=300000

1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<algorithm>
6 using namespace std;
7
8 typedef long long LL;
9 const int N=2*100000,M=30*100000;
10 // const int N=2*300000,M=30*300000;
11 struct node{
12 int x,y,next;
13 }a[N];
14 struct trnode{
15 int lc,rc;
16 LL sum;
17 }t[M];
18 int n,m,num,len,tl;
19 int first[N],dfn[N],edfn[N],dep[N],tot[N],root[N];
20
21 int minn(int x,int y){return x<y ? x:y;}
22
23 void ins(int x,int y)
24 {
25 a[++len].x=x;a[len].y=y;
26 a[len].next=first[x];first[x]=len;
27 }
28
29 int add(int rt,int x,int d)
30 {
31 int now=++tl,tmp=now;
32 int l=1,r=n,mid;
33 while(l<r)
34 {
35 mid=(l+r)/2;
36 if(x<=mid)
37 {
38 r=mid;
39 t[now].lc=++tl;
40 t[tl].lc=t[tl].rc=0;
41 t[now].rc=t[rt].rc;
42 rt=t[rt].lc;
43 now=tl;
44 }
45 else
46 {
47 l=mid+1;
48 t[now].lc=t[rt].lc;
49 t[now].rc=++tl;
50 t[tl].lc=t[tl].rc=0;
51 rt=t[rt].rc;
52 now=tl;
53 }
54 t[now].sum=t[rt].sum+d;
55 }
56 return tmp;
57 }
58
59 LL query(int lx,int rx,int ql,int qr,int l,int r)
60 {
61 if(ql==l && qr==r) return t[rx].sum-t[lx].sum;//debug 一开始更新到了叶子节点。。
62 int mid=(l+r)/2;
63 if(qr<=mid) return query(t[lx].lc,t[rx].lc,ql,qr,l,mid);
64 if(ql>mid) return query(t[lx].rc,t[rx].rc,ql,qr,mid+1,r);
65 return query(t[lx].lc,t[rx].lc,ql,mid,l,mid)+query(t[lx].rc,t[rx].rc,mid+1,qr,mid+1,r);
66 }
67
68 void dfs(int x,int fa)
69 {
70 dep[x]=dep[fa]+1;
71 dfn[x]=++num;
72 tot[x]=1;
73 for(int i=first[x];i;i=a[i].next)
74 {
75 int y=a[i].y;
76 if(y==fa) continue;
77 dfs(y,x);
78 tot[x]+=tot[y];
79 }
80 edfn[x]=num;
81 }
82
83 void build_tree(int x,int fa)
84 {
85 root[dfn[x]]=add(root[dfn[x]-1],dep[x],tot[x]-1);
86 for(int i=first[x];i;i=a[i].next)
87 {
88 int y=a[i].y;
89 if(y==fa) continue;
90 build_tree(y,x);
91 }
92 }
93
94 void output(int x,int l,int r)
95 {
96 printf("x = %d l = %d r = %d lc = %d rc = %d sum = %d\n",x,l,r,t[x].lc,t[x].rc,t[x].sum);
97 int mid=(l+r)/2;
98 if(t[x].lc) output(t[x].lc,l,mid);
99 if(t[x].rc) output(t[x].rc,mid+1,r);
100 }
101
102 int main()
103 {
104 // freopen("a.in","r",stdin);
105 freopen("tree.in","r",stdin);
106 freopen("tree.out","w",stdout);
107 scanf("%d%d",&n,&m);
108 num=0;tl=0;len=0;
109 memset(first,0,sizeof(first));
110 for(int i=1;i<n;i++)
111 {
112 int x,y;
113 scanf("%d%d",&x,&y);
114 ins(x,y);
115 ins(y,x);
116 }
117 dfs(1,0);
118 root[0]=0;t[0].lc=t[0].rc=0;
119 build_tree(1,0);
120 LL ans;int p,k;
121 for(int i=1;i<=m;i++)
122 {
123 scanf("%d%d",&p,&k);
124 ans=((LL)minn(dep[p]-1,k))*((LL)(tot[p]-1));
125 ans+=query(root[dfn[p]],root[edfn[p]],minn(n,dep[p]+1),minn(n,dep[p]+k),1,n);
126 printf("%lld\n",ans);
127 }
128 return 0;
129 }


