【poj2104-求区间第k大数(不修改)】主席树/可持续化线段树
第一道主席树~然而是道比较水的。。。因为它不用修改。。。
转载一个让我看懂的主席树的讲解吧:http://blog.csdn.net/regina8023/article/details/41910615 (未授权,侵权删)
---------------------------------------------------------------------------------------------------------------------
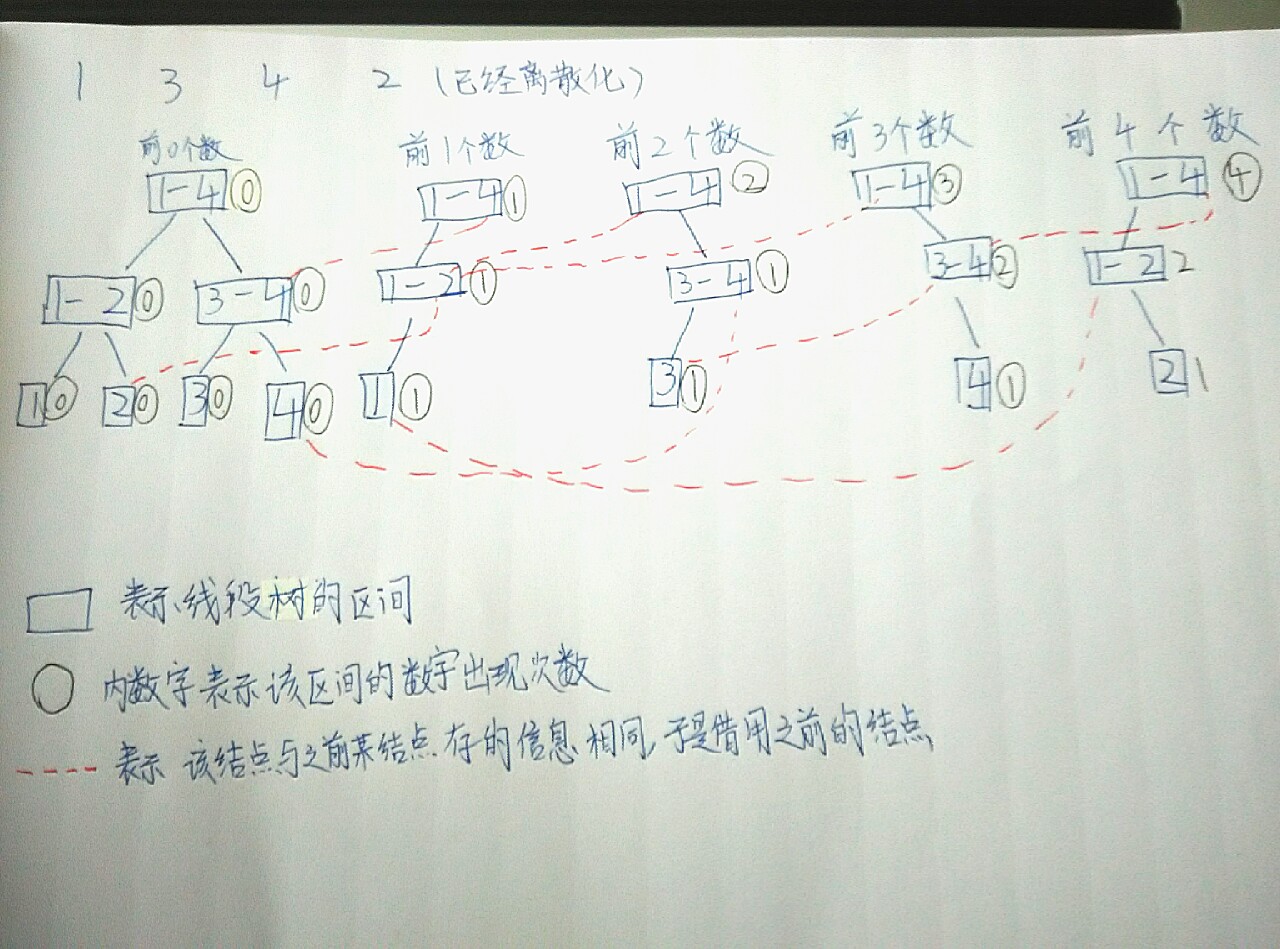
那么如果要询问i-j之间数字出现的次数怎么办呢?
因为每一棵线段树的区间都是相同的,所以要求l-r之间的数字的出现次数只要用前r位出现的次数减去前l-1位出现的次数,就是ans
但是如果有修改操作怎么办?
如果沿用上面的做法,那么修改操作是O(nlogn)的,查询是O(1)的,修改要花好长时间。。。
前缀和联想到了树状数组,那么将前缀和用树状数组维护的话修改是O(logn*logn),查询时O(logn),查询的时间虽然变长,但是修改的时间缩短许多!!
注意:
函数式线段树的数组要开大一点!!
---------------------------------------------------------------------------------------------------------------------
这题就是模版题啦,先离散,求区间第k大的时候lx=root[l-1],rx=root[r],两边同时走不断作差,看看左孩子的数量,如果k更大就减掉左孩子的到有右孩子中找。
代码:
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cmath>
5 #include<iostream>
6 #include<algorithm>
7 using namespace std;
8
9 const int N=100010,INF=(int)1e9+100;
10 struct trnode{
11 int lc,rc,cnt;
12 }t[30*N];
13 struct node{
14 int d,id;
15 }p[N];
16 int n,m,tl,mx;
17 int a[N],num[N],root[N];
18
19 bool cmp(node x,node y){return x.d<y.d;}
20
21 int bt(int l,int r)
22 {
23 int x=++tl;
24 // a[x].l=l;a[x].r=r;
25 t[x].lc=t[x].rc=0;
26 t[x].cnt=0;
27 if(l<r)
28 {
29 int mid=(l+r)/2;
30 t[x].lc=bt(l,mid);
31 t[x].rc=bt(mid+1,r);
32 }
33 return x;
34 }
35
36 int add(int rt,int x)
37 {
38 int now=++tl,tmp=now;
39 t[now].cnt=t[rt].cnt+1;
40 int l=1,r=mx,mid;
41 while(l<r)
42 {
43 mid=(l+r)/2;
44 if(x<=mid)
45 {
46 t[now].lc=++tl;
47 t[now].rc=t[rt].rc;
48 rt=t[rt].lc;
49 now=tl;
50 r=mid;
51 }
52 else
53 {
54 t[now].lc=t[rt].lc;
55 t[now].rc=++tl;
56 rt=t[rt].rc;
57 now=tl;
58 l=mid+1;
59 }
60 t[now].cnt=t[rt].cnt+1;
61 }
62 return tmp;
63 }
64
65 int query(int lx,int rx,int k)
66 {
67 int l=1,r=mx,mid;
68 while(l<r)
69 {
70 mid=(l+r)/2;
71 if(t[t[rx].lc].cnt-t[t[lx].lc].cnt>=k)
72 {
73 r=mid;
74 lx=t[lx].lc;
75 rx=t[rx].lc;
76 }
77 else
78 {
79 l=mid+1;
80 k-=t[t[rx].lc].cnt-t[t[lx].lc].cnt;
81 lx=t[lx].rc;
82 rx=t[rx].rc;
83 }
84 }
85 return l;
86 }
87
88 void output(int x)
89 {
90 printf("x = %d lc = %d rc = %d cnt = %d\n",x,t[x].lc,t[x].rc,t[x].cnt);
91 if(t[x].lc) output(t[x].lc);
92 if(t[x].rc) output(t[x].rc);
93 }
94
95 int main()
96 {
97 freopen("a.in","r",stdin);
98 while(scanf("%d%d",&n,&m)!=EOF)
99 {
100 tl=0;mx=0;
101 for(int i=1;i<=n;i++)
102 {
103 scanf("%d",&a[i]);
104 p[i].d=a[i];p[i].id=i;
105 }
106 sort(p+1,p+1+n,cmp);
107 p[0].d=INF;
108 for(int i=1;i<=n;i++)
109 {
110 if(p[i].d!=p[i-1].d) mx++,num[mx]=p[i].d;
111 a[p[i].id]=mx;
112 }
113 root[0]=bt(1,mx);
114 for(int i=1;i<=n;i++)
115 root[i]=add(root[i-1],a[i]);
116 // output(root[5]);
117 for(int i=1;i<=m;i++)
118 {
119 int l,r,k;
120 scanf("%d%d%d",&l,&r,&k);
121 printf("%d\n",num[query(root[l-1],root[r],k)]);
122 }
123 }
124 return 0;
125 }

