【hdu1542】线段树求矩形面积并
分割线内容转载自http://hzwer.com/879.html
---------------------------------------------------------------------------------
第一次做线段树扫描法的题，网搜各种讲解，发现大多数都讲得太过简洁，不是太容易理解。所以自己打算写一个详细的。看完必会o(∩_∩)o
顾名思义，扫描法就是用一根想象中的线扫过所有矩形，在写代码的过程中，这根线很重要。方向的话，可以左右扫，也可以上下扫。方法是一样的，这里我用的是由下向上的扫描法。
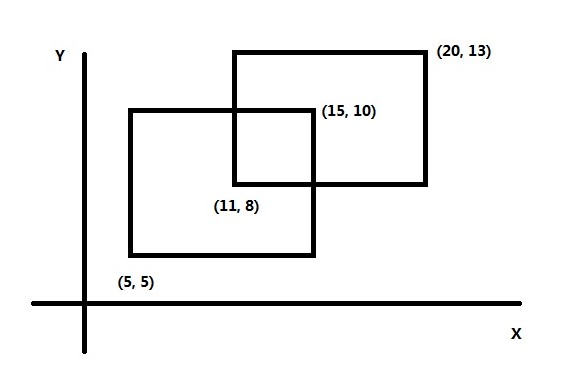
如上图所示，坐标系内有两个矩形。位置分别由左下角和右上角顶点的坐标来给出。上下扫描法是对x轴建立线段树，矩形与y平行的两条边是没有用的，在这里直接去掉。如下图。
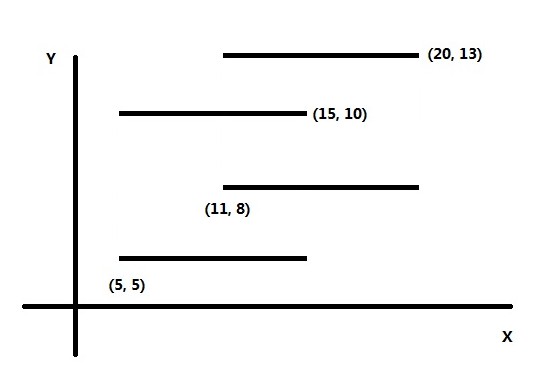
现想象有一条线从最下面的边开始依次向上扫描。线段树用来维护当前覆盖在x轴上的线段的总长度，初始时总长度为0。用ret来保存矩形面积总和，初始时为0。
由下往上扫描，扫描到矩形的底边时将它插入线段树，扫描到矩形的顶边时将底边从线段树中删除。而在代码中实现的方法就是，每条边都有一个flag变量，底边为1，顶边为-1。
用cover数组（通过线段树维护）来表示某x轴坐标区间内是否有边覆盖，初始时全部为0。插入或删除操作直接让cover[] += flag。当cover[] > 0 时，该区间一定有边覆盖。
开始扫描到第一条线，将它压入线段树，此时覆盖在x轴上的线段的总长度L为10。计算一下它与下一条将被扫描到的边的距离S（即两条线段的纵坐标之差，该例子里此时为3）。
则 ret += L * S. （例子里增量为10*3=30）
结果如下图
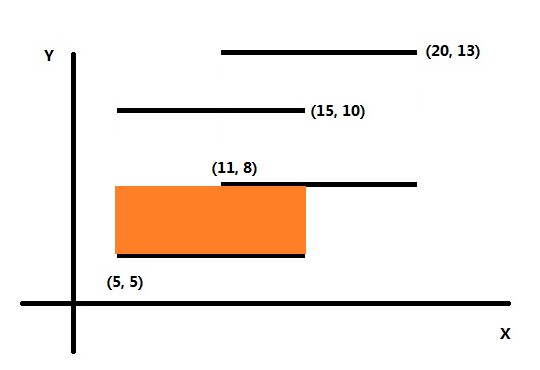橙色区域表示已经计算出的面积。
扫描到第二条边，将它压入线段树，计算出此时覆盖在x轴上的边的总长度。
例子里此时L=15。与下一条将被扫描到的边的距离S=2。 ret += 30。 如下图所示。
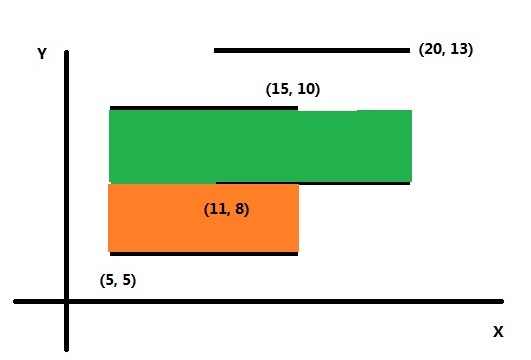绿色区域为第二次面积的增量。
接下来扫描到了下方矩形的顶边，从线段树中删除该矩形的底边，并计算接下来面积的增量。如下图。
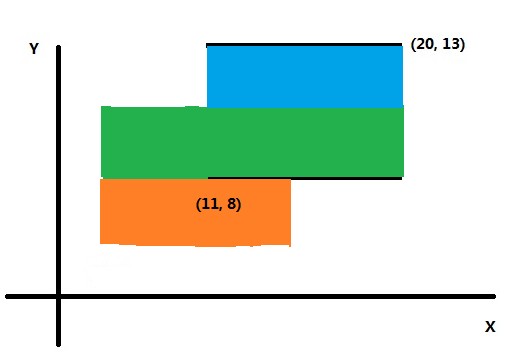蓝色区域为面积的增量。
此时矩形覆盖的总面积已经计算完成。 可以看到，当共有n条底边和顶边时，只需要从下往上扫描n-1条边即可计算出总面积。
此题因为横坐标包含浮点数，因此先离散化。另外，因为用线段树维护的是覆盖在x轴上的边，而边是连续的，并非是一个个断点，因此线段树的每一个叶子结点实际存储的是该点与下一点之间的距离。
12.25
---------------------------------------------------------------------------------
这道题我一直在纠结，怎么求当前有扫描线上有的线段总长？怎么lazy下放？我一直想的是每个点维护的都是它维护的这个区间内的总的cnt等等。
后来我发现换个思路，一切都很简单！
我的每个节点t[x].l~t[x].r维护的其实是线段t[x].l~(t[x].r+1)，也就是若干条线段，因为点分成左右孩子的时候会有问题（比如[3,3]维护的到底是什么？）。
我们要把每个节点看成是一条线段。
对于每个节点维护两个值：
cnt：这个点所代表的线段被覆盖了多少次。
len：以这个点为根的子树中被覆盖的区间一共有多长。
当一条线段进来的时候，在代表它的那若干个节点上cnt++，其它节点cnt不用加。
然后len维护的就是这个区间内那些cnt>0的节点所覆盖的区间总长。
我做惯了叶子节点才有实际意义的线段树，思路太过狭隘，被卡了这么久，其实线段树上每个节点都可以有它的实际意义。
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cmath>
5 #include<iostream>
6 #include<algorithm>
7 using namespace std;
8
9 const int N=1100,INF=(int)1e9;
10 double z[N][4];
11 struct point{
12 double d;
13 int x,y;
14 }p[2*N];
15 struct node{
16 int x0,x1,d;
17 double y;
18 }a[N];
19 struct trnode{
20 int l,r,lc,rc,cnt;
21 double rl,len;
22 }t[2*N];
23 double num[N];
24 int n,tl,pl,al;
25
26 int minn(int x,int y){return x<y ? x:y;}
27 int maxx(int x,int y){return x>y ? x:y;}
28 bool cmp_d(point x,point y){return x.d<y.d;}
29 bool cmp_y(node x,node y){return x.y<y.y;}
30
31 int bt(int l,int r)
32 {
33 int x=++tl;
34 t[x].l=l;t[x].r=r;
35 t[x].lc=t[x].rc=0;
36 t[x].cnt=0;t[x].len=0;
37 t[x].rl=num[r+1]-num[l];
38 if(l<r)
39 {
40 int mid=(l+r)/2;
41 t[x].lc=bt(l,mid);
42 t[x].rc=bt(mid+1,r);
43 }
44 return x;
45 }
46
47 void upd(int x)
48 {
49 int lc=t[x].lc,rc=t[x].rc;
50 if(t[x].cnt>0) t[x].len=t[x].rl;
51 else t[x].len=t[lc].len+t[rc].len;
52 }
53
54 void change(int x,int l,int r,int d)
55 {
56 if(t[x].l==l && t[x].r==r)
57 {
58 t[x].cnt+=d;
59 upd(x);
60 return ;
61 }
62 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
63 if(r<=mid) change(lc,l,r,d);
64 else if(l>mid) change(rc,l,r,d);
65 else
66 {
67 change(lc,l,mid,d);
68 change(rc,mid+1,r,d);
69 }
70 upd(x);
71 }
72
73 int main()
74 {
75 freopen("a.in","r",stdin);
76 int T=0;
77 while(1)
78 {
79 scanf("%d",&n);
80 if(n==0) break;
81 int x,mx;pl=0;tl=0;al=0;t[0].len=0;
82 for(int i=1;i<=n;i++)
83 {
84 for(int j=0;j<=3;j++)
85 {
86 scanf("%lf",&z[i][j]);
87 if(j%2==0) p[++pl].d=z[i][j],p[pl].x=i,p[pl].y=j;
88 }
89 }
90 sort(p+1,p+1+pl,cmp_d);
91 mx=0;p[0].d=INF;
92 for(int i=1;i<=pl;i++)
93 {
94 if(p[i].d!=p[i-1].d) mx++,num[mx]=p[i].d;
95 z[p[i].x][p[i].y]=mx;
96 }
97 bt(1,mx);
98 for(int i=1;i<=n;i++)
99 {
100 if(z[i][1]<z[i][3]) swap(z[i][1],z[i][3]);
101 if(z[i][0]>z[i][2]) swap(z[i][0],z[i][2]);
102 a[++al].x0=z[i][0];a[al].x1=z[i][2];a[al].y=z[i][1];a[al].d=-1;
103 a[++al].x0=z[i][0];a[al].x1=z[i][2];a[al].y=z[i][3];a[al].d=1;
104 }
105 sort(a+1,a+1+al,cmp_y);
106 // for(int i=1;i<=al;i++)
107 // printf("%d -> %d %lf %d\n",a[i].x0,a[i].x1,a[i].y,a[i].d);
108 double w,h,ans=0;
109 change(1,a[1].x0,a[1].x1-1,a[1].d);
110 for(int i=2;i<=al;i++)
111 {
112 h=a[i].y-a[i-1].y;
113 w=t[1].len;
114 ans+=w*h;
115 // printf("w = %lf h = %lf\n",w,h);
116 change(1,a[i].x0,a[i].x1-1,a[i].d);
117 }
118 printf("Test case #%d\nTotal explored area: %.2lf\n\n",++T,ans);
119 }
120 return 0;
121 }
