【bzoj3476-懒惰的奶牛】线段树

题解:
感觉这题和别人的做法不一样。。。呵呵呵。。。调了一百年。。
设家坐标为(a,b),对于每个点(x,y),可以转化为|a-x|+|b-y|<=k
对于每个点,它的影响范围是一个菱形(也就是一个正方形啦。。),也就是一个图上有若干个正方形。
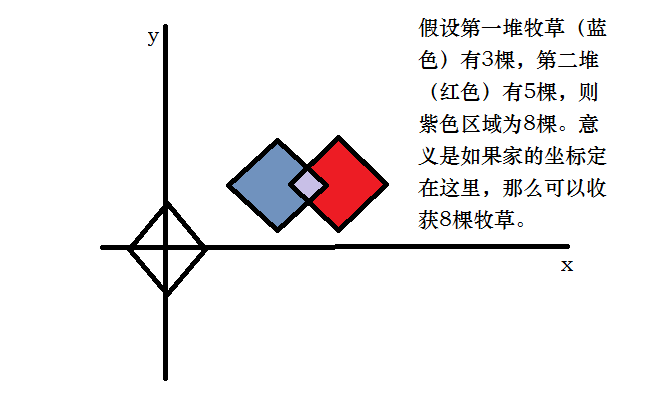
然后我就把这个坐标轴选择了45度。
好难画不画了,正交分解一下就可以了。
然后题目就转化成正方形各种交里的最大值。
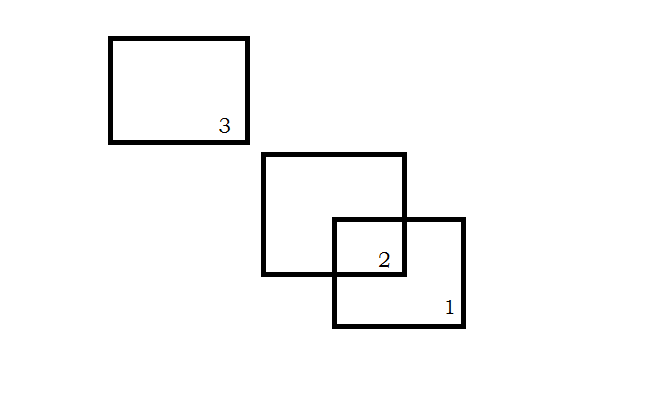
正方形有x和y两个元素,但是很明显我们只能维护一个。。
所以我以x轴建立线段树,对于每个正方形按照y从小到大排序。
维护一个指针j,表示当前前j个正方形已经和现在在处理的第i个正方形没有交集。每次都要先把j更新(看看它是否能后移)。
然后我们在当前正方形的两端a[i].x~a[i].y这一段+a[i].d
每个点维护当前的和d以及该区间的最大值mx。每次做完之后,用t[1].mx更新答案。
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<ctime>
6 #include<queue>
7 #include<algorithm>
8 using namespace std;
9
10 const int N=1001000,INF=(int)1e9;
11 int n,K,L,tl,ans;
12 struct trnode{
13 int l,r,lc,rc,d,mx,lazy;
14 }t[4*N];
15 struct node{
16 int x,y,d;
17 }a[N];
18
19 bool cmp(node x,node y){return x.y<y.y;}
20 int maxx(int x,int y){return x>y ? x:y;}
21 int minn(int x,int y){return x<y ? x:y;}
22
23 int read()
24 {
25 int x=0,f=1; char ch=getchar();
26 while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
27 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
28 return x*f;
29 }
30
31 int bt(int l,int r)
32 {
33 int x=++tl;
34 t[x].l=l;t[x].r=r;
35 t[x].lc=t[x].rc=0;
36 t[x].mx=0;t[x].d=0;
37 t[x].lazy=0;
38 if(l<r)
39 {
40 int mid=(l+r)/2;
41 t[x].lc=bt(l,mid);
42 t[x].rc=bt(mid+1,r);
43 }
44 return x;
45 }
46
47 void pd(int x)
48 {
49 if(t[x].lazy==0) return ;
50 int d=t[x].lazy,lc=t[x].lc,rc=t[x].rc;
51 t[x].lazy=0;
52 t[x].d+=d;
53 t[x].mx+=d;
54 if(lc) t[lc].lazy+=d;
55 if(rc) t[rc].lazy+=d;
56 }
57
58 void change(int x,int l,int r,int d)
59 {
60 pd(x);
61 if(t[x].l==l && t[x].r==r)
62 {
63 t[x].lazy+=d;
64 pd(x);
65 return ;
66 }
67 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
68 if(r<=mid) change(lc,l,r,d);
69 else if(l>mid) change(rc,l,r,d);
70 else
71 {
72 change(lc,l,mid,d);
73 change(rc,mid+1,r,d);
74 }
75 pd(x);pd(lc);pd(rc);
76 t[x].mx=maxx(t[lc].mx,t[rc].mx);
77 }
78
79 int main()
80 {
81 // freopen("a.in","r",stdin);
82 // freopen("me.out","w",stdout);
83 freopen("lazy.in","r",stdin);
84 freopen("lazy.out","w",stdout);
85 n=read();K=read();
86 // scanf("%d%d",&n,&K);
87 int x,y,tx,ty,nx=INF,ny=INF,mx=0;tl=0;L=2*K;
88 for(int i=1;i<=n;i++)
89 {
90 a[i].d=read();x=read();y=read();
91 // scanf("%d%d%d",&a[i].d,&x,&y);
92 tx=x,ty=y+K;
93 a[i].x=tx-ty;
94 a[i].y=tx+ty;
95
96 nx=minn(nx,a[i].x);
97 ny=minn(ny,a[i].y);
98 }
99 for(int i=1;i<=n;i++)
100 {
101 a[i].x-=nx-1;
102 a[i].y-=ny-1;
103 mx=maxx(mx,a[i].x);
104 }
105 mx+=10;ans=0;
106 sort(a+1,a+1+n,cmp);
107 bt(1,mx);
108 int j=1;
109 change(1,a[1].x,minn(mx,a[1].x+L),a[1].d);
110 ans=maxx(ans,t[1].mx);
111 for(int i=2;i<=n;i++)
112 {
113 while(j<i && a[i].y-L>a[j].y)
114 {
115 change(1,a[j].x,minn(mx,a[j].x+L),-a[j].d);
116 ans=maxx(ans,t[1].mx);
117 j++;
118 }
119 change(1,a[i].x,minn(mx,a[i].x+L),a[i].d);
120 ans=maxx(ans,t[1].mx);
121 }
122 printf("%d\n",ans);
123 return 0;
124 }

