【bzoj3387-跨栏训练】线段树+dp

我们可以想到一个dp方程:f[i][0]表示当前在i个栅栏的左端点,f[i][1]表示在右端点。
分两种情况:
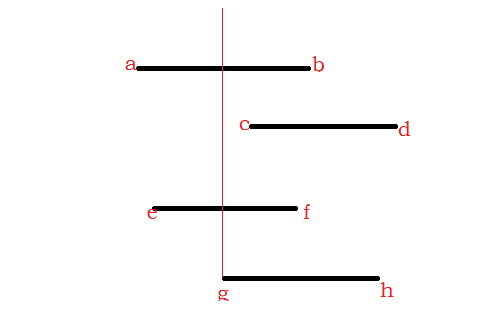
第一种:假设现在要更新线段gh的左端点g,而它下来的路径被ef挡住了,那么必定是有ef来更新g。
为什么呢?因为其它点走到g必定要下落,比如说d到g,就相当于d到f再到g。
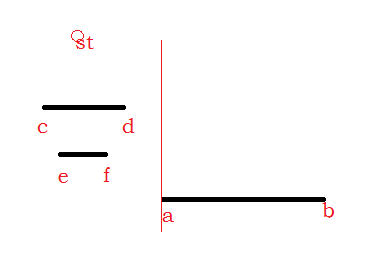
第二种:假设到ab的路径上没有东西挡着,那就可以直接从源点走过去再直接下落。
按照从上到下的顺序插入线段,线段树就是找当前的某个点被哪条id最大(也就是最低的)线段所覆盖。
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 #include<ctime>
6 #include<queue>
7 #include<algorithm>
8 using namespace std;
9
10 const int N=2*2*50010,INF=(int)1e9;
11 int n,st,pl,tl,r[N],f[N][2];
12 struct node{
13 int d,id,tmp;
14 }p[N];
15 struct nd{
16 int x1,x2;
17 }a[N];
18 struct trnode{
19 int l,r,lc,rc,id,lazy;
20 }t[2*N];
21
22 bool cmp_d(node x,node y){return x.d<y.d;}
23 int myabs(int x){return x>0 ? x:-x;}
24 int minn(int x,int y){return x<y ? x:y;}
25 int maxx(int x,int y){return x>y ? x:y;}
26
27 int bt(int l,int r)
28 {
29 int x=++tl;
30 t[x].l=l;t[x].r=r;
31 t[x].lc=t[x].rc=0;
32 t[x].id=INF;t[x].lazy=INF;
33 if(l<r)
34 {
35 int mid=(l+r)/2;
36 t[x].lc=bt(l,mid);
37 t[x].rc=bt(mid+1,r);
38 }
39 return x;
40 }
41
42 void upd(int x)
43 {
44 if(t[x].lazy==INF) return ;
45 int id=t[x].lazy,lc=t[x].lc,rc=t[x].rc;
46 t[x].lazy=INF;
47 t[x].id=minn(t[x].id,id);
48 if(lc) t[lc].lazy=minn(t[lc].lazy,id);
49 if(rc) t[rc].lazy=minn(t[rc].lazy,id);
50 }
51
52 void change(int x,int l,int r,int id)
53 {
54 upd(x);
55 if(t[x].l==l && t[x].r==r)
56 {
57 t[x].lazy=minn(t[x].lazy,id);
58 upd(x);
59 return ;
60 }
61 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
62 if(r<=mid) change(lc,l,r,id);
63 else if(l>mid) change(rc,l,r,id);
64 else
65 {
66 change(lc,l,mid,id);
67 change(rc,mid+1,r,id);
68 }
69 }
70
71 int query(int x,int p)
72 {
73 upd(x);
74 if(t[x].l==t[x].r) return t[x].id;
75 int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/2;
76 if(p<=mid) return query(lc,p);
77 else return query(rc,p);
78 }
79
80 int main()
81 {
82 // freopen("a.in","r",stdin);
83 // freopen("me.out","w",stdout);
84 freopen("obstacle.in","r",stdin);
85 freopen("obstacle.out","w",stdout);
86 scanf("%d%d",&n,&st);
87 int x,ed;ed=0;pl=0;tl=0;
88 p[++pl].d=st;p[pl].id=n+1;
89 p[++pl].d=ed;p[pl].id=n+2;
90 for(int i=1;i<=n;i++)
91 {
92 scanf("%d%d",&a[i].x1,&a[i].x2);
93 if(a[i].x1>a[i].x2) swap(a[i].x1,a[i].x2);
94 p[++pl].d=a[i].x1;p[pl].id=i;p[pl].tmp=0;
95 p[++pl].d=a[i].x2;p[pl].id=i;p[pl].tmp=1;
96 }
97 sort(p+1,p+1+pl,cmp_d);
98 int mx=0;p[0].d=INF;
99 for(int i=1;i<=pl;i++)
100 {
101 if(p[i].d!=p[i-1].d) mx++,r[mx]=p[i].d;
102 if(p[i].id==n+1) st=mx;
103 else if(p[i].id==n+2) ed=mx;
104 else
105 {
106 if(p[i].tmp==0) a[p[i].id].x1=mx;
107 else a[p[i].id].x2=mx;
108 }
109 }
110 bt(1,mx);
111 change(1,st,st,n+1);
112 a[n+1].x1=a[n+1].x2=st;
113 f[n+1][0]=f[n+1][1]=0;
114 a[0].x1=a[0].x2=ed;
115 for(int i=n;i>=0;i--)
116 {
117 x=query(1,a[i].x1);
118 if(x<INF) f[i][0]=minn(f[x][0]+myabs(r[a[x].x1]-r[a[i].x1]),f[x][1]+myabs(r[a[x].x2]-r[a[i].x1]));
119 else f[i][0]=myabs(r[st]-r[a[i].x1]);
120 x=query(1,a[i].x2);
121 if(x<INF) f[i][1]=minn(f[x][0]+myabs(r[a[x].x1]-r[a[i].x2]),f[x][1]+myabs(r[a[x].x2]-r[a[i].x2]));
122 else f[i][1]=myabs(r[st]-r[a[i].x2]);
123 change(1,a[i].x1,a[i].x2,i);
124 }
125 printf("%d\n",f[0][0]);
126 return 0;
127 }

