【hdu3341-Lost's revenge】DP压缩+AC自动机
题意:给定只含有A、G、C、T的n个模板串,一个文本串,文本串任意两个字母可互换位置,问最多能匹配多少个模板串。
注意:匹配同一个模板串匹配了两次,ans+=2;(可重复)
题解:
原本想到一个简单dp : 开一个数组d[t1][t2][t3][t4][x],t1~t4分别表示4个字母各有多少个,x表示当前位置。
然后这个数组为40*40*40*40*600,各种爆空间。
后来才知道要用压缩。。。
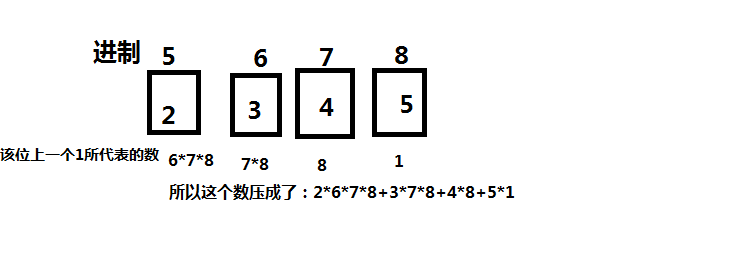
比如ACGT分别有5,6,7,8个。那t1为6进制,可以放0~5,t2为7进制……
然后类比10进制,把它压成一个10进制的数,这个数最大是11*11*11*11=14641.
压缩的原理:
我打了两个程序,dp一个用了递归,一个用了for循环,递归那个一直超时,for那个就A了。递归跟for循环差别这么大吗?
1 //DP为for循环递推形式 AC 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<queue> 7 using namespace std; 8 9 const int N=600; 10 struct node{ 11 int sum,fail,son[5]; 12 }a[N]; 13 queue<int> q; 14 char s[N]; 15 int n,num,t[5],sum[5],k[5],d[15000][N]; 16 bool vis[15000][N]; 17 int maxx(int x,int y){return x>y ? x:y;} 18 int minn(int x,int y){return x<y ? x:y;} 19 20 int idx(char c) 21 { 22 if(c=='A') return 1; 23 if(c=='G') return 2; 24 if(c=='C') return 3; 25 if(c=='T') return 4; 26 } 27 28 void clear(int x) 29 { 30 a[x].fail=a[x].sum=0; 31 memset(a[x].son,0,sizeof(a[x].son)); 32 } 33 34 void trie(char *c) 35 { 36 int x=0,l=strlen(c); 37 for(int i=0;i<l;i++) 38 { 39 int ind=idx(c[i]); 40 if(!a[x].son[ind]) 41 { 42 num++; 43 clear(num); 44 a[x].son[ind]=num; 45 } 46 x=a[x].son[ind]; 47 } 48 a[x].sum++; 49 } 50 51 void buildAC() 52 { 53 while(!q.empty()) q.pop(); 54 for(int i=1;i<=4;i++) 55 if(a[0].son[i]) q.push(a[0].son[i]); 56 while(!q.empty()) 57 { 58 int x=q.front();q.pop(); 59 int fail=a[x].fail; 60 for(int i=1;i<=4;i++) 61 { 62 if(a[x].son[i]) 63 { 64 int y=a[x].son[i],z=a[fail].son[i]; 65 a[y].fail=z; 66 a[y].sum+=a[z].sum; 67 q.push(a[x].son[i]); 68 } 69 else a[x].son[i]=a[fail].son[i]; 70 } 71 } 72 } 73 74 int makeup() 75 { 76 return t[1]*k[1]+t[2]*k[2]+t[3]*k[3]+t[4]*k[4]; 77 } 78 79 int dp() 80 { 81 memset(d,-1,sizeof(d)); 82 d[0][0]=0; 83 int ans=0,ss=sum[1]+sum[2]+sum[3]+sum[4]; 84 for(int l=0;l<=ss;l++)//当前选择了多少个点 85 for(int i=0;i<=num;i++)//当前走到了第i个点 86 for(t[1]=maxx(0,l-sum[2]-sum[3]-sum[4]);t[1]<=minn(l,sum[1]);t[1]++)//限制 最少选多少 最多选多少 87 for(t[2]=maxx(0,l-t[1]-sum[3]-sum[4]);t[2]<=minn(l,sum[2]);t[2]++) 88 for(t[3]=maxx(0,l-t[1]-t[2]-sum[4]);t[3]<=minn(l,sum[3]);t[3]++) 89 { 90 t[4]=l-t[1]-t[2]-t[3]; 91 int now=makeup(); 92 if(d[now][i]==-1) continue; 93 ans=maxx(ans,d[now][i]); 94 for(int j=1;j<=4;j++) 95 { 96 int y=a[i].son[j]; 97 if(t[j]+1<=sum[j]) 98 { 99 t[j]++; 100 int next=makeup(); 101 d[next][y]=maxx(d[next][y],d[now][i]+a[y].sum); 102 t[j]--; 103 } 104 } 105 } 106 return ans; 107 } 108 109 int main() 110 { 111 freopen("a.in","r",stdin); 112 freopen("a.out","w",stdout); 113 int T=0; 114 while(1) 115 { 116 scanf("%d",&n); 117 if(!n) return 0; 118 num=0; 119 clear(0); 120 for(int i=1;i<=n;i++) 121 { 122 scanf("%s",s); 123 trie(s); 124 } 125 buildAC(); 126 scanf("%s",s); 127 int mx=0,l=strlen(s); 128 memset(sum,0,sizeof(sum)); 129 memset(vis,0,sizeof(vis)); 130 for(int i=0;i<l;i++) sum[idx(s[i])]++; 131 for(int i=1;i<=4;i++) 132 { 133 k[i]=1; 134 for(int j=i+1;j<=4;j++) 135 k[i]*=(sum[j]+1); 136 mx+=k[i]*sum[i]; 137 } 138 printf("Case %d: %d\n",++T,dp()); 139 } 140 return 0; 141 }
1 //DP为递归形式 TLE 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<queue> 7 using namespace std; 8 9 const int N=600; 10 struct node{ 11 int sum,fail,son[5]; 12 }a[N]; 13 queue<int> q; 14 char s[N]; 15 int n,num,t[5],sum[5],k[5],d[15000][N]; 16 bool vis[15000][N]; 17 int maxx(int x,int y){return x>y ? x:y;} 18 int minn(int x,int y){return x<y ? x:y;} 19 20 int idx(char c) 21 { 22 if(c=='A') return 1; 23 if(c=='G') return 2; 24 if(c=='C') return 3; 25 if(c=='T') return 4; 26 } 27 28 void clear(int x) 29 { 30 a[x].fail=a[x].sum=0; 31 memset(a[x].son,0,sizeof(a[x].son)); 32 } 33 34 void trie(char *c) 35 { 36 int x=0,l=strlen(c); 37 for(int i=0;i<l;i++) 38 { 39 int ind=idx(c[i]); 40 if(!a[x].son[ind]) 41 { 42 num++; 43 clear(num); 44 a[x].son[ind]=num; 45 } 46 x=a[x].son[ind]; 47 } 48 a[x].sum++; 49 } 50 51 void buildAC() 52 { 53 while(!q.empty()) q.pop(); 54 for(int i=1;i<=4;i++) 55 if(a[0].son[i]) q.push(a[0].son[i]); 56 while(!q.empty()) 57 { 58 int x=q.front();q.pop(); 59 int fail=a[x].fail; 60 for(int i=1;i<=4;i++) 61 { 62 if(a[x].son[i]) 63 { 64 int y=a[x].son[i],z=a[fail].son[i]; 65 a[y].fail=z; 66 a[y].sum+=a[z].sum; 67 q.push(a[x].son[i]); 68 } 69 else a[x].son[i]=a[fail].son[i]; 70 } 71 } 72 } 73 74 int makeup(int t1,int t2,int t3,int t4) 75 { 76 return t1*k[1]+t2*k[2]+t3*k[3]+t4*k[4]; 77 } 78 79 int dp(int now,int x) 80 { 81 int ans=0,t1,t2,t3,t4; 82 if(vis[now][x]) return d[now][x]; 83 t4=now%k[3]; 84 t3=((now%k[2])-(t4*k[4]))/k[3]; 85 t2=((now%k[1])-(t4*k[4]+t3*k[3]))/k[2]; 86 t1=(now-(t4*k[4]+t3*k[3]+t2*k[2]))/k[1]; 87 for(int i=1;i<=4;i++) 88 { 89 int y=a[x].son[i]; 90 if(!y && x) ans=maxx(ans,dp(now,0)); 91 else if(i==1 && t1>=1) ans=maxx(ans,a[y].sum+dp(makeup(t1-1,t2,t3,t4),y)); 92 else if(i==2 && t2>=1) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2-1,t3,t4),y)); 93 else if(i==3 && t3>=1) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2,t3-1,t4),y)); 94 else if(i==4 && t4>=1) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2,t3,t4-1),y)); 95 } 96 d[now][x]=maxx(d[now][x],ans); 97 vis[now][x]=1; 98 return d[now][x]; 99 } 100 101 int main() 102 { 103 freopen("a.in","r",stdin); 104 freopen("a.out","w",stdout); 105 int T=0; 106 while(1) 107 { 108 scanf("%d",&n); 109 if(!n) return 0; 110 num=0; 111 clear(0); 112 for(int i=1;i<=n;i++) 113 { 114 scanf("%s",s); 115 trie(s); 116 } 117 buildAC(); 118 scanf("%s",s); 119 int mx=0,l=strlen(s); 120 memset(sum,0,sizeof(sum)); 121 memset(vis,0,sizeof(vis)); 122 for(int i=0;i<l;i++) sum[idx(s[i])]++; 123 for(int i=1;i<=4;i++) 124 { 125 k[i]=1; 126 for(int j=i+1;j<=4;j++) 127 k[i]*=(sum[j]+1); 128 mx+=k[i]*sum[i]; 129 } 130 // printf("%d\n",dp()); 131 memset(d,0,sizeof(d)); 132 printf("Case %d: %d\n",++T,dp(mx,0)); 133 } 134 return 0; 135 }

