struc2vec 论文阅读

论文目的

强调依据的 Graph 中的 structure info 对于 Node 的分类。这区别于以往的假设 “相邻较近的节点具有相似的分类情况”
即用 “structure identity”。换句话说————“struc2vec is superior in a classification task where node labels depends more on structural identity”

实现方式

如何衡量结构相似性

从直觉上来说，两个 Node 如果是结构相似的，那么他们应该会有相近的度。进一步来说，如果这两个 Node 的相互的 neighbors 同样也有相近的度，那么可以说这两个 Node 的结构相似性更高了。【有点类似于 neighbors consensus】

具体来说，记
\(k\) 为某个节点的 k-hop（\(k\) 阶邻居）
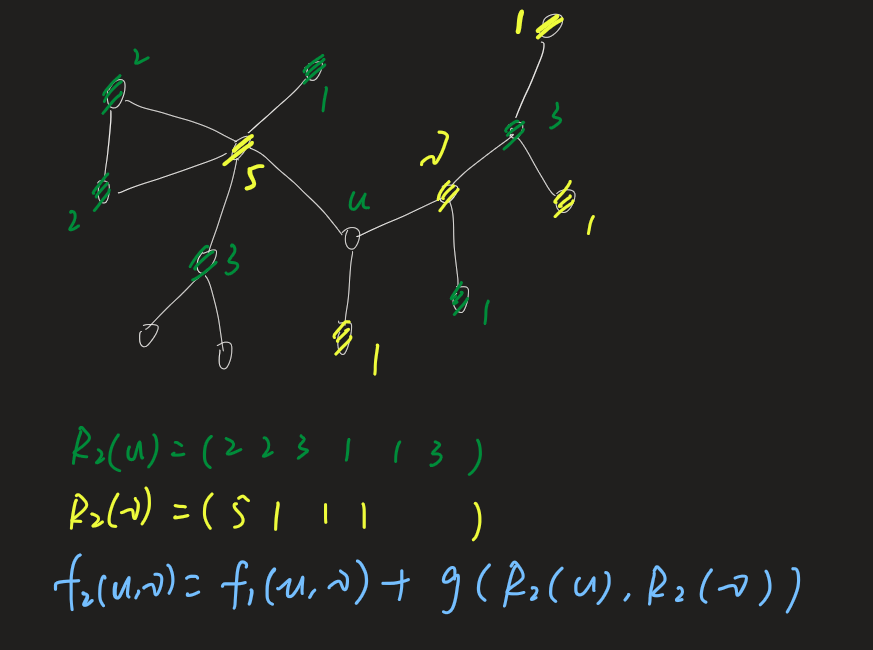
\(R_k(u)\) 代表节点 u 的 k 阶邻居集合【the ring of nodes at distance k】
\(s(S)\) 对节点集合 S 按照度进行排序

下面公式衡量节点 u 和 v 之间的相似度：

\[\begin{aligned} f_{k}(u, v)=f_{k-1}(u, v)+g\left(s\left(R_{k}(u)\right), s\left(R_{k}(v)\right)\right) &, \\ k \geq 0 \text { and }\left|R_{k}(u)\right|,\left|R_{k}(v)\right|>0 \end{aligned}\]

这是一个递归式。\(f_{-1}=0\)。\(g(D_1, D_2) \geq 0\) 表示度序列 \(D_{1}\) 和 \(D_{2}\) 之间的 distance. \(g(D_1, D_2)\) 该值越大则序列差异越大。 【方便理解：类似衡量cosx 和 sinx 的差异度】
总之：\(f_{k}(u,v)\) 值越小，则节点 u 和 v 结构相似度越高

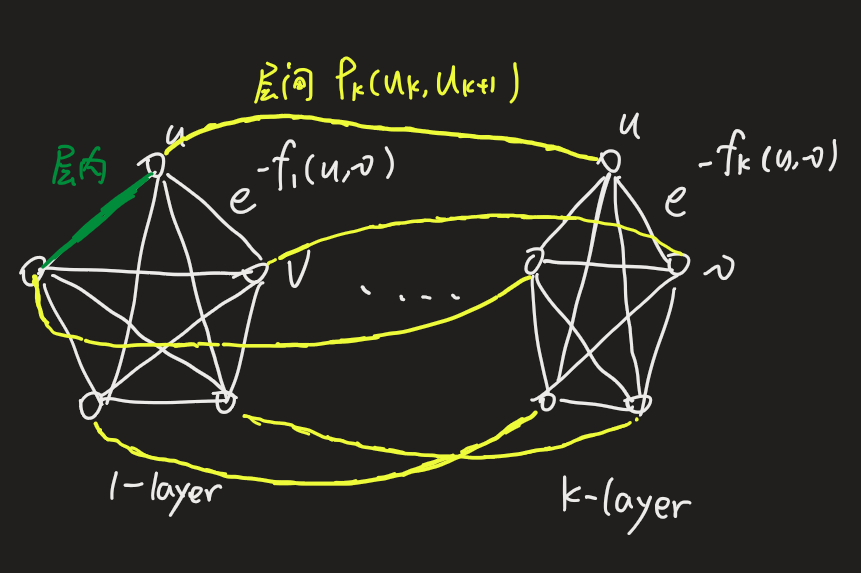
构建上下文图（context graph）

层内

观察上一节的公式，其中 k 是 k-hop，所以这一节，将针对 k=0,1,2....\(k^*\) 分别构建一个 context graph
同时如果两个节点之间有 edge，那么给这条 edge 赋一个权重值 \(w_{k}(u, v)\)（用于下文的随机游走）

\[w_{k}(u, v)=e^{-f_{k}(u, v)}, \quad k=0, \ldots, k^{*} \]

可以看到，\(f_k\) 越小 ==> 节点结构越相似 ==> \(w\) 越大 ==> 则权重值越大(用于随机游走)

层间

那么 \(k\) 的变动，会有不同的层，不同层之间 graph 结构是不变的（类似堆成的千层饼），所以不同层之间同一个节点我们添加两条通路：

\[\begin{array}{l} w\left(u_{k}, u_{k+1}\right)=\log \left(\Gamma_{k}(u)+e\right), \quad k=0, \ldots, k^{*}-1 \\ w\left(u_{k}, u_{k-1}\right)=1, \quad k=1, \ldots, k^{*} \end{array} \]

其中

\[\Gamma_{k}(u)=\sum_{v \in V} \mathbb{1}\left(w_{k}(u, v)>\overline{w_{k}}\right) \]

\[\overline{w_{k}}=\sum_{(u, v) \in\left(\begin{array}{c} v \\ 2 \end{array}\right)} w_{k}(u, v) /\left(\begin{array}{l} n \\ 2 \end{array}\right) \]

\(\overline{w_{k}}\) 是该层的平均权重，所以第一个式子表示，如果该层的\(\Gamma_{k}(u)\)较大，也就是该层同 u 节点结构相似的数量较多，该层的k-hop，的 k 需要变大，这样包含的结构信息将会更多，才会找到更高层次的 structural similarity

随走游走

通过以上，我们构建了层内和层间的权重连边，这一切都是为了最终的随机游走
每一跳，可能会在层内游走，假设概率 \(q\) ，也可能会在层间 \(1-q\)

层内

\[p_{k}(u, v)=\frac{e^{-f_{k}(u, v)}}{Z_{k}(u)} \]

\[Z_{k}(u)=\sum_{v \in V \atop v \neq u} e^{-f_{k}(u, v)} \]

其中第一个式子就是节点 u 到 v 在 k 层的游走概率

层间

\[\begin{aligned} p_{k}\left(u_{k}, u_{k+1}\right) &=\frac{w\left(u_{k}, u_{k+1}\right)}{w\left(u_{k}, u_{k+1}\right)+w\left(u_{k}, u_{k-1}\right)} &= \frac{\log \left(\Gamma_{k}(u)+e\right)}{\log \left(\Gamma_{k}(u)+e\right)+1} \\ p_{k}\left(u_{k}, u_{k-1}\right) &=1-p_{k}\left(u_{k}, u_{k+1}\right) \end{aligned} \]

可以看到第一个式子，如果该层同 u 相似的节点越大，则大概率可能往上走，即该式子 \(p_{k}\left(u_{k}, u_{k+1}\right)\) 较大

优化算法

优化DTW

上文的计算序列差异的 \(g(s(R_{k}(u)), s(R_{k}(v)))\) 的计算过程中，使用的是DTW算法。在这个计算过程中需要计算一个距离矩阵。作者就对这个距离矩阵的进行了优化。例如，节点 v 的邻居度为4 4 5，对这个序列进行压缩，<度，出现次数数>，<4, 2>,<5,1>
具体计算公式（用于计算距离矩阵）

\[\operatorname{dist}(\boldsymbol{a}, \boldsymbol{b})=\left(\frac{\max \left(a_{0}, b_{0}\right)}{\min \left(a_{0}, b_{0}\right)}-1\right) \max \left(a_{1}, b_{1}\right) \]

\(\boldsymbol{a}=\left(a_{0}, a_{1}\right) \text { and } \boldsymbol{b}=\left(b_{0}, b_{1}\right) \text { are tuples in } A^{\prime} \text { and } B^{\prime}\)
\(A^{\prime} \text { and } B^{\prime}\) 是压缩之后的元组序列

优化节点对

上文已经知道，我们在 k 层中，需要对每一对节点进行计算权重，而其实有一些节点对如果在 k=0 初始层的时候，就已经相差较大，则没必要在 k=1... 层之后不断去计算。比如 n 节点度为1，v节点度为10.
所以在该网络中对所有节点按照度排序，然后按照二分查找，来确定 u 和哪些节点需要计算一个相似度

减少层数

但是几层最好呢——对于不同场景，可以测试较优情况

推荐阅读

https://blog.acolyer.org/2017/09/15/struc2vec-learning-node-representations-from-structural-identity/ 图文并茂

论文代码

https://github.com/leoribeiro/struc2vec
将部分代码修改成python3支持的即可运行。看了一下代码，写的还是很清晰的，这里就不贴出来解读了~

验证实验