瑞丽熵 -Variational Characterization of Eigenvalues

结论 ：

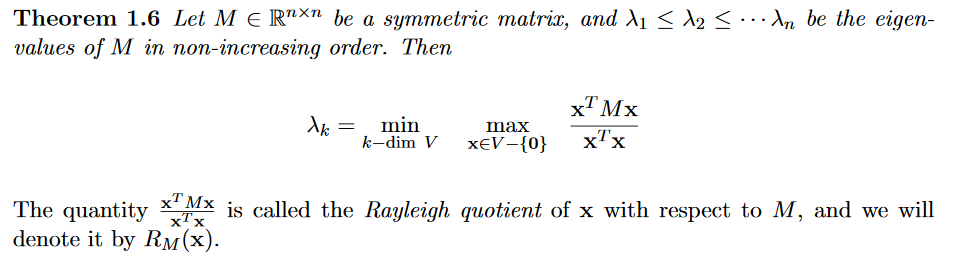
证明 ：

令 \(v_1...v_n\) 是对应的 \(\lambda1...\lambda n\) 的 单位特征向量 。现考虑由 \(v_1...v_k\) 展成的 \(k-dimensional \ space\)，在此空间中的每个向量 \(x = \sum_{i=1}^k a_iv_i\)。

则此时分子为:

\[x^TMx=\sum_{i,j=1}^k a_ia_jv_i^TMv_j=\sum_{i,j=1}^k a_ia_jv_i^T \lambda_j v_j=\sum_{i=1}^ka_i^2\lambda_jv_i^Tv_i \leq \sum_{i=1}^ka_i^2\lambda_k \]

而分母为：

\[x^Tx=\sum_{i,j=1}^k a_ia_jv_i^Tv_j=\sum_{i=1}^k a_i^2 \]

===>

\[\frac{x^TMX }{x^Tx} \leq \lambda_k \]

而且此时的\(x\)取值正好为 \(\lambda_k\) 对应的特向 \(v_k\):

\[\frac{v_k^TMv_k}{v_k^Tv_k}=\frac{v_k^T\lambda_kv_k}{ \| v_k\| }= \lambda_k \]

再考虑 \(min\) 一项：
令 \(v_k...v_n\) 是对应的 \(\lambda k...\lambda n\) 的 单位特征向量 。考虑此时 \(n-k+1\)个向量展成的 \(k-dimensional \ space\)，此空间同上文空间有交集，

因为\(v_k\) 都在两个空间中，令其他特向系数为 \(0\)，则为交集，取其中式子为 $x= \sum_{i=k}^n a_iv_k=a_iv_k $，则容易得到（因为特征向量大小排序已定）：

\[\frac{x^TMX }{x^Tx} \geq \lambda_k \]

推广 ：

要使得 \(max R_m(x)\) 则只需将上文 \(k=n\) ，即瑞丽熵最大取值为\(M\)的最大特征向量对应的特征值

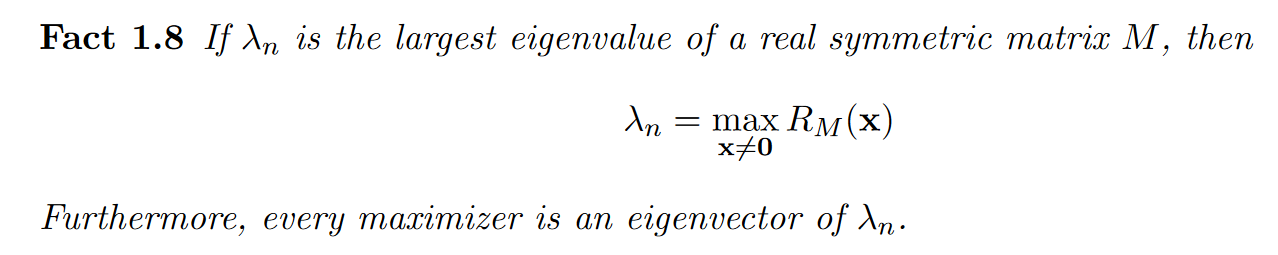
参考 ：
Rayleigh quotient