《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》论文阅读(二)
GCN的定义
下面内容参考kipf博客,个人认为是告诉你从直觉上,我们怎么得到GCN图上的定义(而前面的大幅推导是从理论上一步一步来的,也就是说可以用来佐证我们的直觉)
我们的网络输入是\(\mathcal{G}=(\mathcal{V},\mathcal{E})\):
- 即可以用\(N\times D\)的矩阵\(X\)表示,\(N\)为图上结点个数,\(D\)是每个结点的特征维数
- 同时表示一个图还需要邻接矩阵\(A\)
而一层的输出记作\(Z_{\mathbb{R}^{N \times F}}\),其中\(N\)还是结点个数,\(F\)为每个结点的特征维数
那么非线性神经网络就可以定义成如下形式:
其中\(H^{0}=X\), \(H^{L}=Z\), \(L\) 表示网络的层数,那么模型的关键是如何设计\(f(\cdot )\)
一种简单的形式
其中\(W^{l}\) 是\(l.th\)层的参数矩阵,\(\sigma ()\) 是激活函数。【PS:Despite its simplicity this model is already quite powerful】
仔细观察上式就能发现几个缺陷:
- 其中\(A\)是邻接矩阵,对角线上为\(0\),导致经过网络中的一层,没有加上自己本结点的信息,所以改造替换成 \(\hat{A} = A+I\)
- 可是\(\hat {A}H\) 则是自己+相邻结点特征总和,还需平均化,所以改成 \(D^{-1}\hat {A}H\)
- 我们还可以更进一步,考虑到上篇说的拉普拉斯算子计算中周围结点总和\(-\)中心点*相邻结点个数,即相当于每个相邻点能量\(-\)中心点能量。类比过来,相邻点给我影响是:(相邻点能量/相邻点本身邻居个数),所以有\(D^{-1/2}\hat{A}D^{-1/2}\)
这个形式已经和上篇利用谱理论推导处理的结果很相近了
但和最终的结果还不一样,回顾论文给的 renormalization trick:
那么的确可以得到最终形式:
WEISFEILER-LEHMAN算法
作者试图使用Weifeiler-Lehman算法来解释GCN的表征能力。\(WL\)算法是用来判断两个graph是否同构(简单说是两图拓扑结构相同)的,WL算法

算法包含两个关键点
- 聚合自己和邻接结点信息,若记\(h\_aggregate^{t}_{i}\),\(t\)是第几次迭代,\(i\) 是第几个结点
- 利用hash函数吐出唯一的值,\(h^{t+1}_{i}=hash(h\_aggregate^{t}_{i})\) 代替\(i\) 结点的特征
然后循环迭代
下面一个简单小例子(默认各个结点信息是相同的,所以序号均标为1,主要判断拓扑结构是否同构):
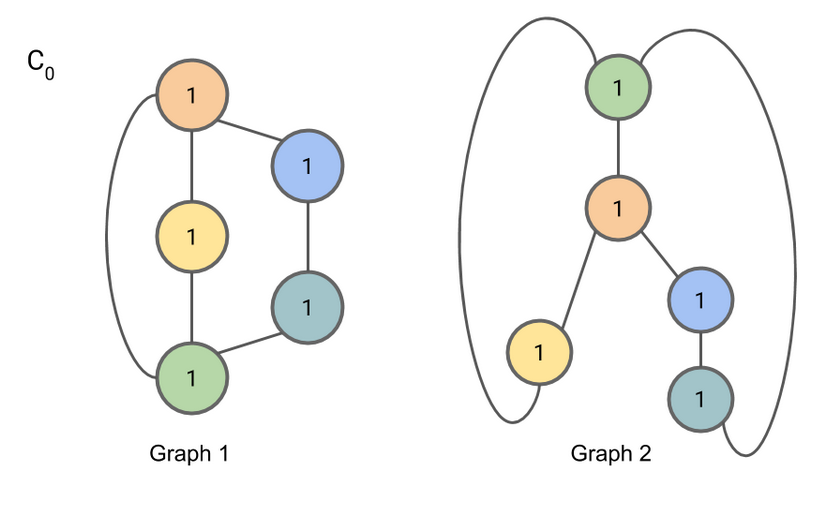
进行信息聚合,因为默认结点是一致的,所以主要通过邻接关系判断是否同构,\(\{1,1,1\}\)即是该结点的相邻结点是谁
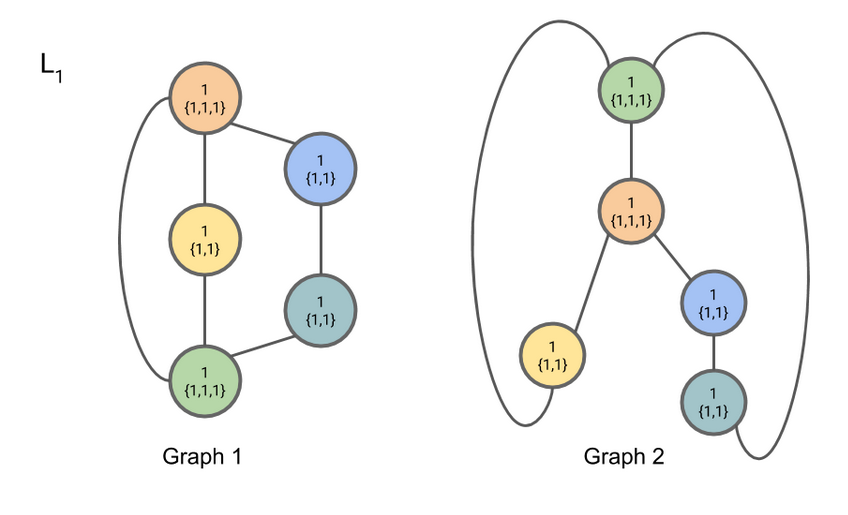
输入hash()函数,并且代替原有结点信息
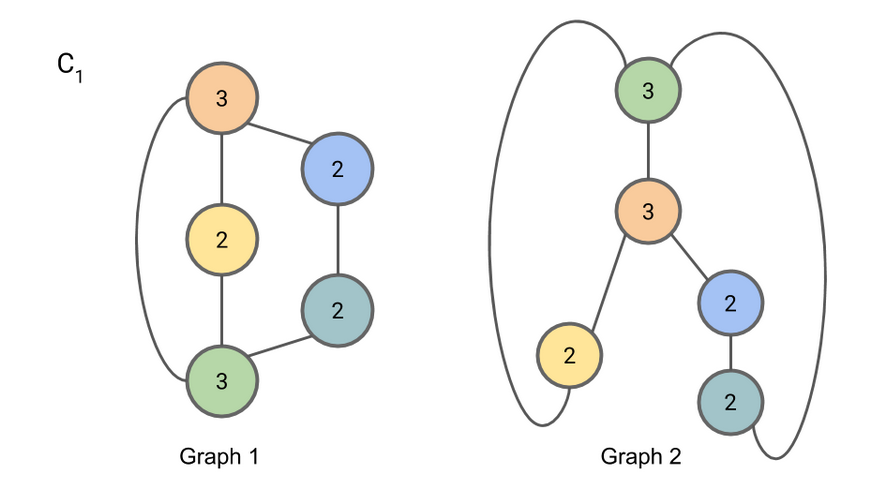
重复上述操作(具体参见:https://www.davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/#)
最后结果:

通过判断 \(9,8,7\) 两个图个数相同,判断是同构
WEISFEILER-LEHMAN算法反映什么
\(WL\)算法由于\(hash()\)函数的使用,使得通过不断迭代,能够表征不能不同结点的差异——即结点自身信息+结点的邻居所带来的差异
代替WL的hash()函数
\(N_{i}\)是结点\(j\)的相邻结点,上式可进一步化成矩阵形式
通过调整\(W^{l}\)参数,实现\(hash()\)的功能。也就是说这种形式的GCN对结点的表征能力可以达到hash()函数级别,作者借此来证明GCN的能力。
可是有个疑问吧,这里用的是\(D^{-1/2}AD^{-1/2}\),其实和上文提到的\(\tilde{D}^{-1/2}\hat{A}\tilde{D}^{-1/2}\),也还是有区别的,前者不是GCN的最终形式。。。。
Zachary karate club举例
任务内容是酱紫的,一共有0~33位俱乐部成员,由于0号和33号两位之间发生了冲突,导致其他成员进行围绕这两位进行了“拉帮结派”,不同成员之间有一定交流(用连线表示),所以任务具体来说就是需要我们对这些成员进行分类——归属于哪个小团体。
我们先看一下label的真实分类情况:
import matplotlib.pyplot as plt
import networkx as nx
from networkx import karate_club_graph, to_numpy_matrix
import matplotlib.pyplot as plt
def lable_graph(G):
fig,ax = plt.subplots()
pos = nx.kamada_kawai_layout(G) # 指定图的美化排列方式
cluter1 = []
cluter2 = []
for i in range(G.number_of_nodes()):
if zkc.nodes[i]['club'] == 'Mr. Hi':
cluter1.append(i)
else:
cluter2.append(i)
nx.draw_networkx_nodes(G, pos, nodelist=cluter1, node_color='orange')
nx.draw_networkx_nodes(G, pos, nodelist=cluter2, node_color='red')
nx.draw_networkx_labels(G, pos, labels={i:str(i) for i in range(G.number_of_nodes())}, font_size=16)
nx.draw_networkx_edges(G, pos, edgelist=G.edges())
zkc = karate_club_graph()
lable_graph(zkc)
plt.show()
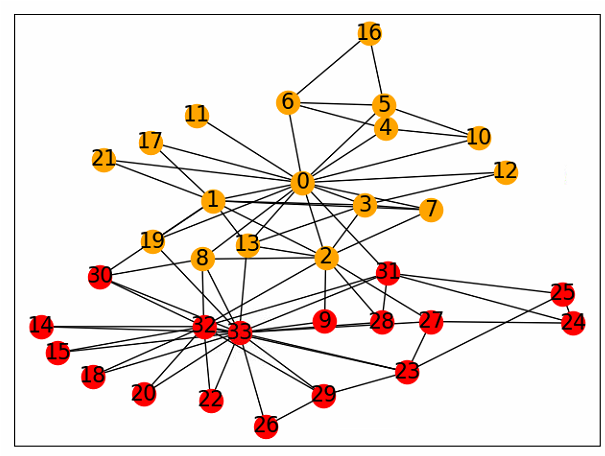
假设暂时采用的形式进行研究:
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from networkx import karate_club_graph, to_numpy_matrix
# np.set_printoptions(threshold=np.inf)
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order) # type=np.matrix
I = np.eye(A.shape[0])
A_hat = A + I
D_hat = np.diag(np.array(np.sum(A_hat, 0)).reshape(-1,))
# print(D_hat, D_hat.shape)
W1 = np.random.normal(loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W2 = np.random.normal(loc=0, scale=1, size=(W1.shape[1], 2))
def relu(x):
return 1 / (1 + np.exp(-x))
# return np.maximum(x, 0)
def gcn_layer(D_hat, A_hat, X, W):
D_hat_1 = np.linalg.inv(D_hat)
result = np.dot(D_hat_1, A).dot(X).dot(W)
return relu(result)
H1 = gcn_layer(D_hat, A_hat, I, W1)
H2 = gcn_layer(D_hat, A_hat, H1, W2)
output = H2 # 34*2
# print(output, output.shape)
pos_weight = {
node: (np.array(output)[node][0], np.array(output)[node][1])
for node in zkc.nodes()}
def plot_graph_feature(G, pos_weight):
fig, ax = plt.subplots()
clsuter1 = []
clsuter2 = []
for i in range(G.number_of_nodes()):
if G.nodes[i]['club'] == 'Mr. Hi':
clsuter1.append(i)
else:
clsuter2.append(i)
nx.draw_networkx_nodes(G, pos_weight, nodelist=clsuter1, node_color='orange')
nx.draw_networkx_nodes(G, pos_weight, nodelist=clsuter2, node_color='red')
nx.draw_networkx_labels(G, pos_weight, labels={i: str(i) for i in range(G.number_of_nodes())}, font_size=16)
nx.draw_networkx_edges(G, pos_weight, edgelist=G.edges())
ax.set_title('epoch')
# x1_min = x1_max = pos_weight[0][0]
# x2_min = x2_max = pos_weight[0][1]
# for index,pos in pos_weight.items():
# x1_min = np.minimum(x1_min, pos[0])
# x1_max = np.maximum(x1_max, pos[0])
# x2_min = np.minimum(x2_min, pos[1])
# x2_max = np.maximum(x2_max, pos[1])
# ax.set_xlim(x1_min, x1_max)
# ax.set_ylim(x2_min, x2_max)
plot_graph_feature(zkc, pos_weight)
plt.show()
如上,采用随机初始化参数,配套使用两层GCN,根据\(WL\)理论,的确可以得到比较良好的分类结果(当然下图也是随机得到的比较理想的情况),但是我们都还没开始反向传播呢,效果有点闪瞎狗眼
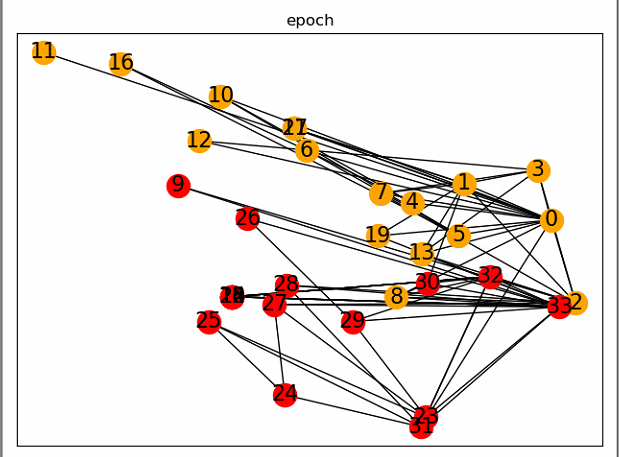
使用DGL框架实现
实现如下,总的来说,只使用了两个结点的label,最后的效果还是挺吃惊的,大有文章
import dgl
import numpy as np
import networkx as nx
import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl.nn.pytorch import GraphConv
import itertools
import matplotlib.pyplot as plt
def build_karate_club_graph():
src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10,
10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21,
25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32,
32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33,
33, 33, 33, 33, 33, 33, 33, 33, 33, 33])
dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4,
5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23,
24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23,
29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30,
31, 32])
# Edges are directional in DGL; Make them bi-directional.
u = np.concatenate([src, dst])
v = np.concatenate([dst, src])
# Construct a DGLGraph
return dgl.DGLGraph((u, v))
def lable_gt_graph(G):
fig, ax = plt.subplots()
pos = nx.kamada_kawai_layout(G) # 指定图的美化排列方式
cluter1 = []
cluter2 = []
for i in range(G.number_of_nodes()):
if G.nodes[i]['club'] == 'Mr. Hi':
cluter1.append(i)
else:
cluter2.append(i)
nx.draw_networkx_nodes(G, pos, nodelist=cluter1, node_color='orange')
nx.draw_networkx_nodes(G, pos, nodelist=cluter2, node_color='red')
nx.draw_networkx_labels(G, pos, labels={i: str(i) for i in range(G.number_of_nodes())}, font_size=16)
nx.draw_networkx_edges(G, pos, edgelist=G.edges())
G = build_karate_club_graph()
# print('We have %d nodes.' % G.number_of_nodes())
# print('We have %d edges.' % G.number_of_edges())
nx_G = G.to_networkx().to_undirected()
# pos = nx.kamada_kawai_layout(nx_G)
# nx.draw(nx_G, pos, with_labels=True) # 未分类的
# plt.show()
embed = nn.Embedding(34, 5) # 随机初始化
G.ndata['feat'] = embed.weight
# print(G.ndata['feat'][2])
class GCN(nn.Module):
def __init__(self, in_feat, hidden_size, num_classes):
super(GCN, self).__init__()
self.conv1 = GraphConv(in_feat, hidden_size)
self.conv2 = GraphConv(hidden_size, num_classes)
def forward(self, g, inputs):
h = self.conv1(g, inputs)
h = torch.relu(h)
h = self.conv2(g, h)
return h
net = GCN(5, 5, 2)
inputs = embed.weight
labeled_nodes = torch.tensor([0, 33])
labels = torch.tensor([0, 1])
optimizer = torch.optim.Adam(itertools.chain(net.parameters(), embed.parameters()), lr=0.01)
all_logits = []
for epoch in range(50):
logits = net(G, inputs)
all_logits.append(logits.detach())
logp = F.log_softmax(logits, 1) # dimension
loss = F.nll_loss(logp[labeled_nodes], labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))
fig, ax = plt.subplots()
def draw(i):
cls1color = 'orange'
cls2color = 'red'
pos = {}
colors = []
for v in range(34):
pos[v] = all_logits[i][v].numpy()
cls = pos[v].argmax()
colors.append(cls1color if cls else cls2color)
ax.set_title('Epoch: %d' % i)
nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
node_size=300, with_labels=True)
plt.show()
draw(5)
draw(49)
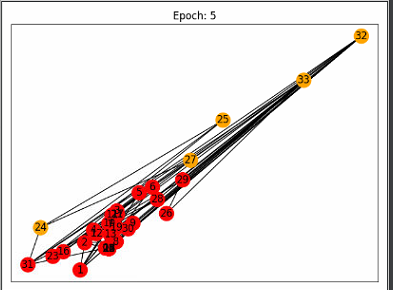
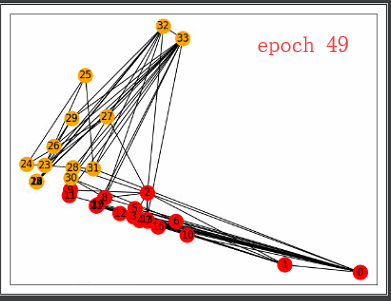
参考
https://www.zhihu.com/question/54504471
http://tkipf.github.io/graph-convolutional-networks/
https://www.davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/#


