2.8模拟赛 赛后题解

难度排序

T4<T2<T1<T3

最高得分：

前5名：

T4

由题意不难知道，每次选择拔高的区间的右端点一定是$n$，具体证明大家意会一下...

考虑$f[i][j]$表示当前选择的左区间最右不超过$i$且拔高了$j$次的答案

则$$f[i][j]=max{f[x][y]}+1(x<i,y \leq j,a[x]+y \leq a[i]+j)$$

二位树状数组维护一下即可

（看！树套树！）

时间复杂度$O(nk \cdot lognlogk)$

T2

不难想到我们换字符时的策略

(1)我们只会把别的字符换成$b_i$因为换其它字符对答案没有贡献

(2)我们不会创造许多隔开的$b_i$因为同样对答案没有贡献

于是我们考虑暴力

当我们面对一个询问$(a,b)$时我们看每一个$[l,r]$看可不可以把它用$m$次操作全变成$b$

预处理每一段区间$b$出现的次数$t_b$即可Check的时候只需看$(r-l+1)-t_b$是否$\leq m$即可

预处理时可以前缀地预处理出$[1,i]$中$b_i$的出现次数用于更新

实战中这个$O(n^2 \cdot q)$的算法好像可以跑过所有测试点...也不知道什么原理

我的做法是优化这个暴力

我们二分答案

然后枚举长度最大的串出现的位置

由于预处理出了$[1,i]$中每个$b_i$的出现次数

我们可以很快的check

由于答案不超过$n$我们可以$O(nqlog n)$过掉这道题

T1

罕见的不能区间减的数位dp

其实选这道题的时候考虑过很多版本，有很简单适合当T1的，有这道题稍加改动的。

但后来要么太简单要么太难（树套树优化树形数位dp你们知道有多酸爽不）

最后千万考虑还是放了这道原题

这道题是SGU390

bzoj题号忘了是什么了，反正题目名字应该叫“我爸是李刚”

集训队的题，思想方法比较成熟，我就不要越俎代庖了

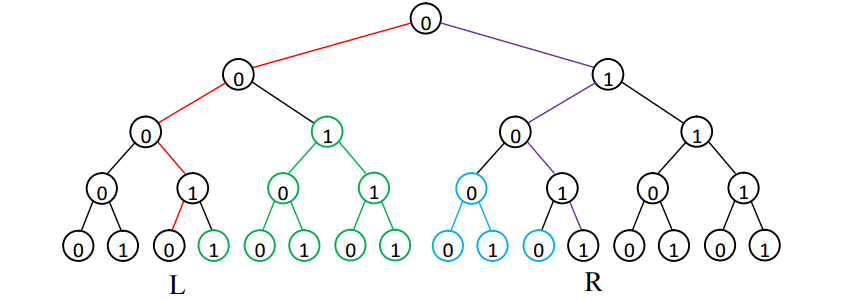
T4

原题HNOI2016最小公倍数

考虑暴力做法，对于每一个询问，暴力加入满足询问的边，然后维护联通性和$maxp，maxq$，如果满足条件则$Yes$。 
两个条件的限制似乎很难用别的数据结构优化掉，那么考虑分块，先以$p$为第一关键字，$q$为第二关键字排序，每$m^{0.5}$分成一块。然后把每一个询问归类到相应的块中，使得这个询问的$p$大于等于块的$p$最小值小于等于最大值。 
依次扫每个块，把每个块的询问取出来。设当前的块号是$i$,那么我们把$1$到$i-1$的块里面的所有的边按$b$排序，

再把这个块内的询问按$q$排序。然后扫$1$到$i-1$的符合当前询问的边，加入并查集。对于i块内的边，只能暴力扫然后加入并查集了，注意处理完这个询问后，要撤销掉在该块内加入的边。

所以此题的并查集不能路径压缩，要用启发式合并或按秩合并，两者都是$logn$的，总的时间复杂度时$O(n^{1.5}logn)$。