莫比乌斯反演

http://www.bilibili.com/video/av14325327/

懒得听我bb的可以去看视频 这位大爷讲的太好辣orz

我突然意识到我一个还挣扎在NOIP一等奖线上的弱鸡竟然突然学会了

赶紧码着别忘了。。。

 

一、莫比乌斯反演是什么

如果有两个定义在Z+上的函数F(x)和G(x)满足

 

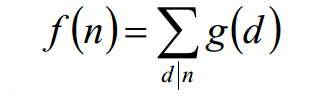
则根据这个式子我们可以发现一些性质    如下图：

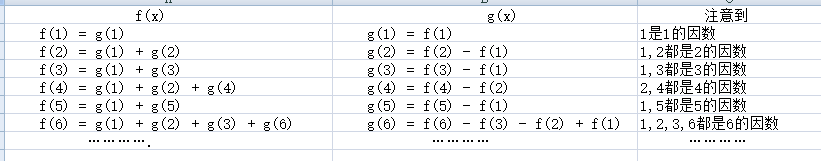
所以以后我们遇到计算G(x)不好算(或者更实际一点，直接算就TLE)的时候，我们可以考虑先计算F(x)   用F(x)来计算G(x)

 

所以我们要对上面那个式子进行一下变形

观察表格的规律  直观的来讲变形后式子应该形如

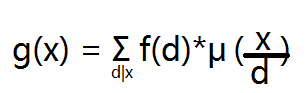
其中μ(x)是我们强行定义的一个函数  当然并不是我们定义的 是前人定义的  所以它正式的名字叫做莫比乌斯函数

然后我们做一下换元 令T=x/d

就可以让最后μ函数中不含x 最后的表达式为

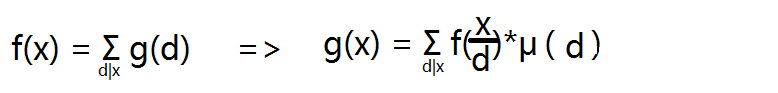
（并非严谨证明    详细过程可见百度百科http://baike.baidu.com/link?url=gpiZ99LcvuK_Vf7K4KszIWRgmmRQkcIpyir9IgzBkyaA3FgVCAG7mouZNVzkZgqyYWdNYUpIwFOixrM6fc8fb_#3 ）

现在  我们研究的重点就跑到了这个μ(d)上面

到目前为止  我们掌握的性质就只有由观察得到的：μ(d)的值域为{-1,0,1}（当然严谨数学证明依然见百度百科）

如：

μ(1) = 1

μ(2) = -1

μ(3) = -1

μ(4) = 0

μ(5) = -1

μ(6) = 1

（上述6个莫比乌斯函数的取值是由表格得到的）

我很想给出莫比乌斯函数的定义 但是我一个前MO选手现NOIP选手自己都看不懂

所以只能给一个通俗的解释

(1) d = 1时，μ(d) = 1

(2) d = p1 × p2 × … × pk ，（其中p1,p2..pk是互不相同的质数） 则μ(d) = (-1)^k （-1的k次方）

(3) 其余情况 μ(d) = 0

根据定义 莫比乌斯函数显然有一个很重要的性质

莫比乌斯函数是积性函数

即对于任何的a,b∈Z+

有μ(ab)=μ(a)μ(b)

具体证明。。。代入就好了吧

由此引入我们的下一个板块

二、怎么求莫比乌斯函数

根据莫比乌斯函数的积性和它与素数间的关系

我们可以用线性筛求素数的方法来求莫比乌斯函数

bool vis[MAXN];
int primes[MAXN];
int miu[MAXN];
int tot;
int getmiu(int lim)
{
    miu[1]=1;
    for(int i=2;i<=lim;i++)
    {
        if(!vis[i])
        {
            primes[tot++]=i;
            miu[i]=-1;
        }
        for(int j=0;j<tot;j++)
        {
            int k=i*primes[j];   
            if(k>lim)break;
            vis[k]=true;
            if(i%primes[j])         //i不是primes[j]的整数倍时,i*primes[j]就不会包含相同质因子.
                miu[k]=-miu[i];     //此时根据其积性函数的特性得 miu[k]=miu[i]*miu[primes[j]],因为primes[j]是质数,miu值为-1
            else break;                
        }
    }
}

很短  压一下行也就10行  于是大家会产生疑惑  就是下一个板块——

三、莫比乌斯函数在OI中的应用

由于很多很难的数学题推导过程写得比代码还长

我们这里先看一道入门题BZOJ2440

题意：求第k个没有完全平方因子（此处1不算完全平方数）的数

k的范围是10^9

分析：有人说答案应该小于2*k  那这道题就是一个很裸的二分了

二分判定的时候要判“小于等于mid且无完全平方因子的数的个数”

判断的时候  我们可以发现“没有完全平方因子”的意思其实是“所有质因数的指数全为奇”

于是题目变为 求小于等于mid的质因数指数都为1的数的个数

容斥原理搞一下答案就是n-奇数个质数的平方的倍数的个数+偶数个质数的平方的倍数的个数

也就是

（显然i如果大于根号n并不存在）

要说还有什么值得注意的地方 就是这题爆longlong 要用unsigned longlong

还有就是数据太大 我们的线性筛用不了 只能采用普通筛法

/**************************************************************
    Problem: 2440
    User: Ez3real
    Language: C++
    Result: Accepted
    Time:4192 ms
    Memory:2068 kb
****************************************************************/
 
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define LL unsigned long long
const int Max=100010;
const LL INF=2e16+7;
 
LL mou[Max];
void init()
{
    for(LL i=2; i<Max; i++)
    {
        if(!mou[i])
        {
            mou[i]=i;
            for(LL j=i*i; j<Max; j+=i)
                mou[j]=i;
        }
    }
    mou[1]=1;
    for(int i=2; i<Max; i++)
    {
        if(i/mou[i]%mou[i]==0) mou[i]=0;
        else mou[i]=-mou[i/mou[i]];
    }
}
int k;
LL getnum(LL middle)
{
    LL ans=0;
    for(LL i=1; i*i<=middle; i++)
    {
        ans+=mou[i]*(middle/(i*i));
    }
    return ans;
}
int main()
{
    init();
    int t;
    cin>>t;
    while(t--)
    {
        scanf("%d",&k);
        LL left=1,right=INF;
        while(left<=right)
        {
            int middle=(left+right)/2;
            if(getnum(middle)<k)
                left=middle+1;
            else
                right=middle-1;
        }
        cout<<left<<'\n';
    }
    return 0;
}

未完待续