Lending Club 数据做数据分析&评分卡

一 ：项目目的

       研究Lending Club 贷款的风险特征，并提出建模方案。

二：数据获取

       数据集来自Lending Club平台发生借贷的业务数据，2017年第一季度，具体数据集可以从Lending Club官网下载,需要先用邮箱注册一个账号。

三：数据探索

     1.导入需要用到的工具

         

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')  #风格设置
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
import warnings
warnings.filterwarnings('ignore') 
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题

      2.导入数据

      

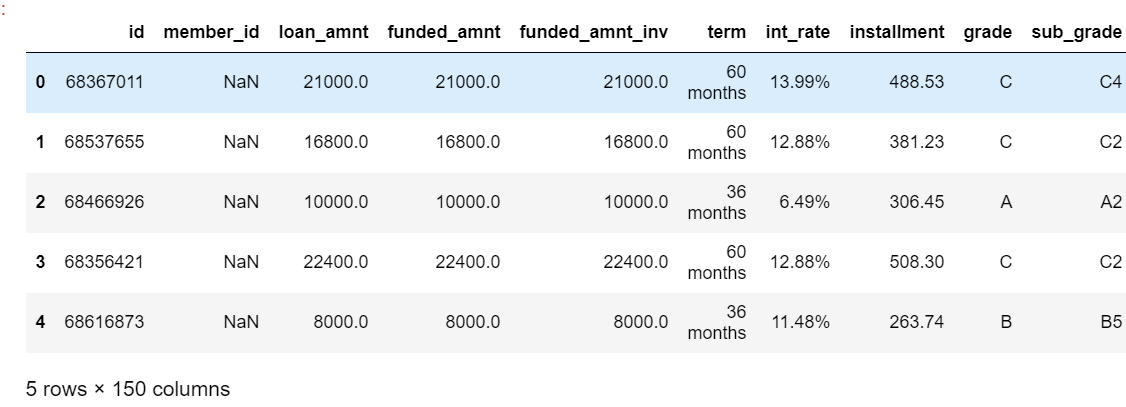
data=pd.read_csv("LoanStats3d_securev1.csv",encoding='latin-1',skiprows = 1)
data.head()

           各个变量的解释也可以在Lending Club 官网找到，直接下载是EXCEL格式的

#看一下目标特征
data.loan_status.value_counts()

Fully Paid            307831
Charged Off            77884
Current                33584
Late (31-120 days)      1006
In Grace Period          436
Late (16-30 days)        287
Default                   67
Name: loan_status, dtype: int64

Fully Paid:已结清 ,Charged Off：坏账 ,Current：当前已还款 , Late (31-120 days)：预期30-120天

#In Grace Period ：已逾期但在宽限期类 , Default：逾期超过90天

#参考：https://help.bitbond.com/article/20-the-10-loan-status-variants-explained·

  从结果看出 我们的正反案列存在严重的正反案列不均衡问题，后续建模需要处理以下

   3.先把标签处理一下    

#封装一个替换函数
def coding(col, codeDict):
　　colCoded = pd.Series(col, copy=True)#创建一个和loan_status一样的 Series
   for key, value in codeDict.items():#返回可遍历的(键, 值) 元组数组
       colCoded.replace(key, value, inplace=True)#替换原有数据
   return colCoded

##把贷款状态LoanStatus编码为违约=1, 正常=0:
dict1={'Current':0,'Fully Paid':0,'Charged Off':1,'Late (31-120 days)':1,'Late (16-30 days)':1,'In Grace Period':1,"Default":1}data["loan_status_class"]=coding(data["loan_status"],dict1)

data.loan_status_class.value_counts()

0    341415
1     79680
Name: loan_status_class, dtype: int64
3.处理缺失值

#查看缺失值
for i in data.columns:
    miss=data[i].isnull().sum()
    print(i,"\t",miss)

 截图不完整

发现很多变量全为空，这种数据对我们没有任何价值，先处理掉这些无用数据。

#删除缺失别列0.8以上的列
half_count = len(data)*0.8 # 设定阀值
data = data.dropna(thresh = half_count, axis = 1 ) #若某一列数据缺失的数量超过阀值就会被删除
data.shape

#data = data.drop(['desc', 'url'，'id'], axis = 1) #删除了一些无用列

（421095, 93）  
#剩下93 列
4.数据描述
  由于数据特征较多，这里筛选一些变量做描述

col=["loan_amnt","term","int_rate","grade","emp_length","annual_inc","verification_status","loan_status","purpose","dti","delinq_2yrs","inq_last_6mths",'open_acc',"pub_rec","revol_bal","total_acc","total_rev_hi_lim","addr_state","home_ownership","emp_title","loan_status_class"]
df=data[col]   

df.columns=["申请额度","借款期限","利率","评级","工作年限","年收入","收入来源是否核实","借款状态","借款目的","负债率","近两年逾期30天以上的次数","近6个月征信查询次数","未结清借款数","负面记录","未结清借款总额","剩余信用额度","总授信额度","所在地","住房状态","职位","分类"]

#描述分类属性依据好坏样本的分布情况
cla=["借款期限","评级","工作年限","收入来源是否核实","借款目的","住房状态"]
for i in cla:
    pvt=pd.pivot_table(df[["分类",i]],index=i,columns="分类",aggfunc=len) 
    pvt.plot(kind="bar")

 

 

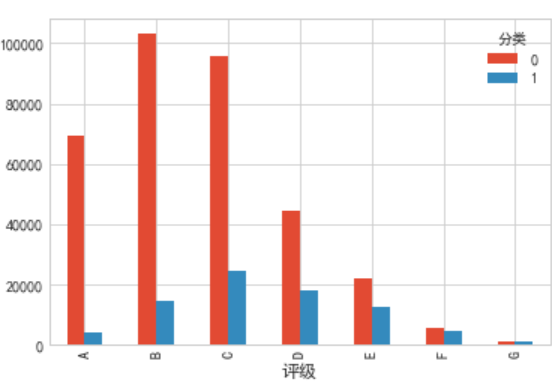
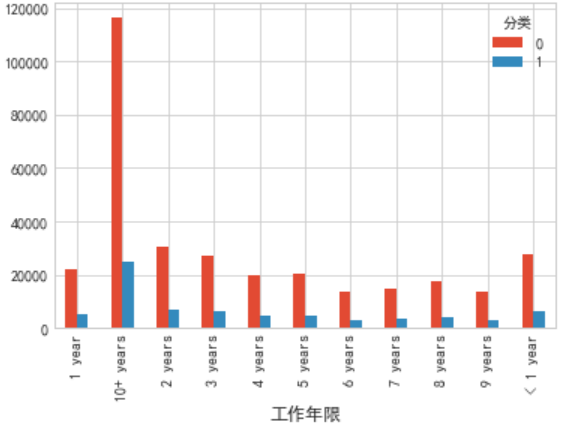
由图可知：
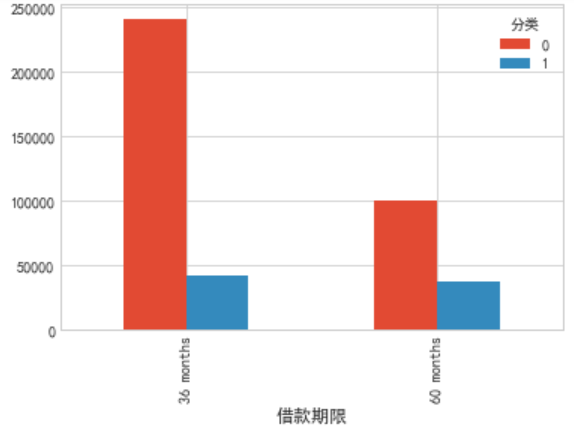
1.（左上）大部分人选择36期贷款，少部分选择60期，但是60期逾期百分比明显高于36期，并且高达37%,借款时间越长，风险越大。
2.（右上）LC自评等级，这个评级与利息相关的，随着评级下降风险越来越高，利息越来越高，我们可以认为相应的逾期率较大，本图也反馈了LC 评级的优异性能
3.（左下）值得注意的是，工作年限10年以上的借款人相对较多，这与我们的一般认知不符合，除此以外工作1-9年的人群随着工作年限加长，借款需求相对减少，可能是收入相对稳定了，
  （题外话：如果这个假设成立，为什么我自己工作年限越长，就越穷呢，是因为能力么，我太难了=。=）
4.（右下）收入来源是否经过核实，大部分是经过核实的，并且经过核实的违约概率相对较低

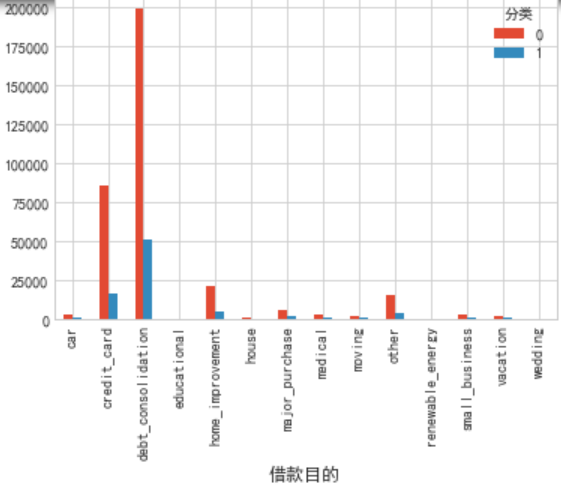
5.借款目的   债务整合，家具装修，还信用卡，三类最多（还是比较诚实，这也侧面说明 这个特征可能用处不大）

6.住房状态上      按揭 与租房 最多，相对的 租房违约率较高 （符合一般家庭情况）

对数值型数据进行描述

cel=[i for i in df1.columns if df1[i].dtypes =="float"]
for i ,j in enumerate(cel):
    plt.figure(figsize=(8,5*len(cel)))
    plt.subplot(len(cel),1,i+1)
    sns.distplot(df1[j][df1.分类==0],color="b")
    sns.distplot(df1[j][df1.分类==1],color="r")

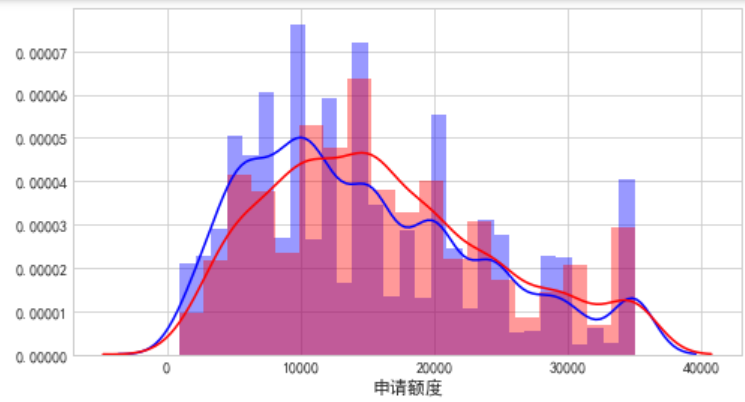
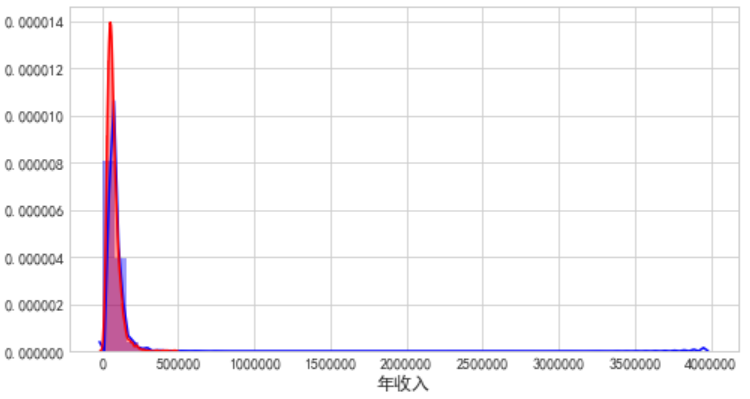
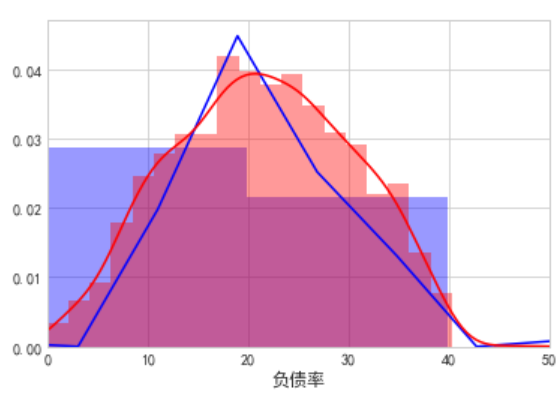
 由图可知：

     1.（左上）借款额度呈正太分布，稍有一点左偏，表明业务多集中在中小额度上面，且额度越高逾期率相对有所增加。

     2.（右上）年收入集中在15万以内，个别极高收入达到400万。

     3.（左下）负债率呈现正太分布，多集中在40%以内

     4.（右下）近两年逾期30天以上的次数，说明即使一次逾期记录也没有，客户也是可能逾期的

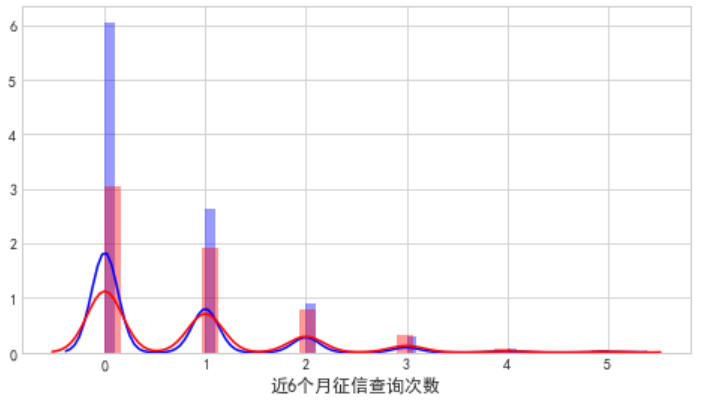
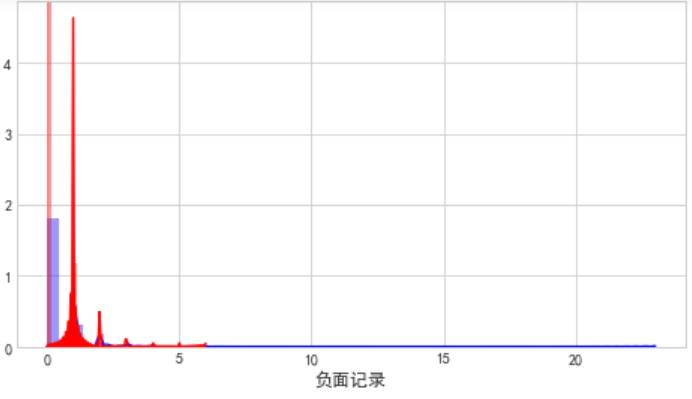
 由图可知：

     1.征信查询，查的越多越容易逾期

      2.没有负面记录也是会逾期的，但是有负面记录的人逾期率要高得多。

用词云图看看，申请地与职位的频率

text=["职位","所在地"]
str_list=["",""]
for i,j in enumerate(text):
    for k in df1[j].values:
        str_list[i]+=str(k) + " "
print(str_list)

#分别设置了背景颜色，宽度，与高度
from wordcloud import WordCloud
wordcloud=WordCloud(background_color="white",width=1000, height=860, margin=2).generate(str_list[0])
plt.imshow(wordcloud)
plt.axis("off")

wordcloud=WordCloud(background_color="white",width=1000, height=860, margin=2).generate(str_list[1])
plt.imshow(wordcloud)
plt.axis("off")
#在制作词云图时，文本之间提前预留空格，作图时间会非常快，相当于自己提前分词

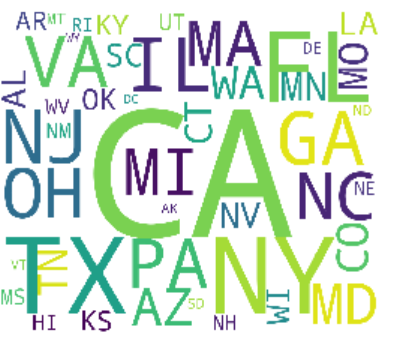
 1.借款人 职务 大多是公司职员，

 2.借款人主要集中在，加利福利亚，纽约 德克萨斯州（该公司中部在加州）

探索借款用途与利率之间的关系

df['int_rate_num'] = df['int_rate'].str.rstrip("%").astype("float")# 删除 利率后面的百分号，并且转换成 浮点型数据
sns.boxplot(y="purpose",x="int_rate_num",data=df)

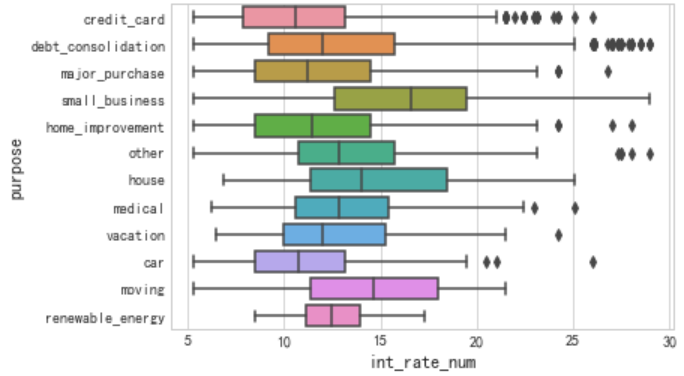
 借款用途为 small_business 的借款利率最高

 探索探索利率 收入 工作年限 和借款状态之间的关系

#替换数据的第二种方法
mapping_dict = {
    "emp_length": {
        "10+ years": 10,
        "9 years": 9,
        "8 years": 8,
        "7 years": 7,
        "6 years": 6,
        "5 years": 5,
        "4 years": 4,
        "3 years": 3,
        "2 years": 2,
        "1 year": 1,
        "< 1 year": 0,
        "n/a": 0
    }
}

df = df.replace(mapping_dict) #转换
df["annual_inc"]=df["annual_inc"].astype("float") #把收入中odjest 转换成float
sns.pairplot(df, vars=["int_rate_num","annual_inc", "emp_length"],hue="loan_status_class", diag_kind="kde" ,kind="reg", size = 3)

 

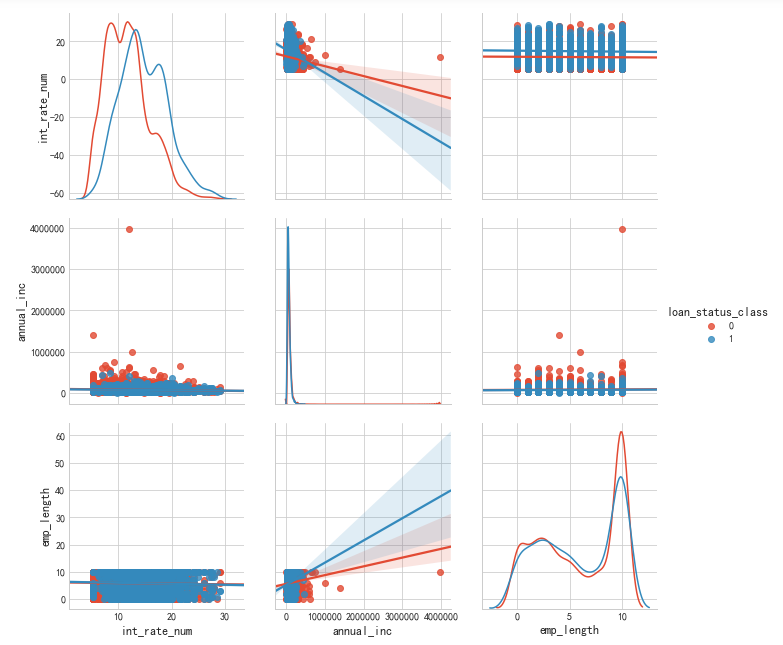
 可理解为 工作年限越长，收入越高违约情况相对较低，相应的享受更低的利息

 

 简单看看相关性

sns.heatmap(df1.corr())

 

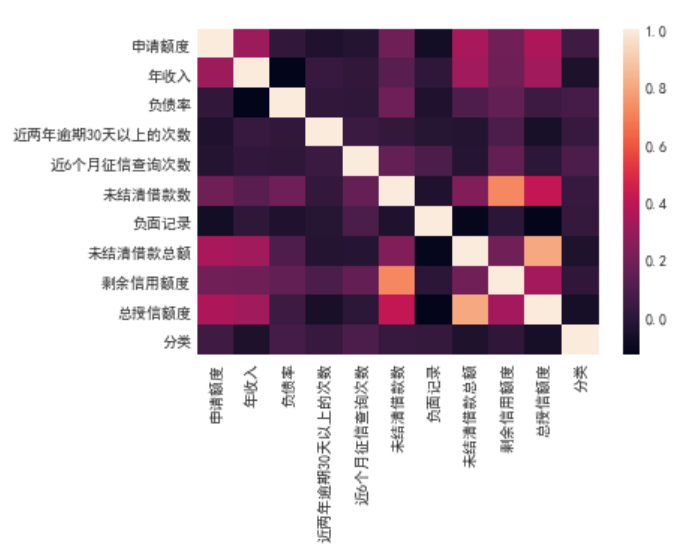
 除去对角线以外颜色越浅相关信息越高

 5.建模准备工作

     1.查看缺失值具体情况，并决定填充策略    

#查看缺失值情况并决定哪些需要删除
data_defect=[i for i in data.columns if (data[i].isnull().sum())/data.shape[0] != 0]
for i in data_defect:
defect=data[i].isnull().sum()/data.shape[0]
print( i , defect)

data=data.drop(["mths_since_recent_bc","mths_since_recent_inq"],axis=1)

#众数填充
fil=["emp_title","emp_length","title","dti","num_rev_accts","num_tl_120dpd_2m","percent_bc_gt_75"]
from scipy.stats import mode # 计算众数模块
for i in fil:
    data[i][data[i].isnull()]=mode(data[i][data[i].notnull()])[0][0]

#再看看缺失值情况

objectcolumns=[i for i in data.columns if data[i].dtype=="object"]
data[objectcolumns].isnull().sum().sort_values(ascending=False)

data[objectcolumns].head()

#发现 int_rate    与revol_util  实际数数值，但是含有% 被识别为字符，借款周期需要处理，工龄需要处理
data.int_rate= data.int_rate.str.rstrip('%').astype('float')
data.revol_util= data.revol_util.str.rstrip('%').astype('float')#删除末尾指定字符，并转化成数值
data["term"]=data["term"].str.rstrip("months").astype("float")
objectcolumns=[i for i in data.columns if data[i].dtypes=="object"]
data[objectcolumns].isnull().sum().sort_values()

#数据过滤
var = data[objectcolumns].columns
for v in var:
    print('\nFrequency count for variable {0}'.format(v))
    print(data[v].value_counts())
data[objectcolumns].shape

drop_list=["sub_grade","title","zip_code","last_pymnt_d","last_credit_pull_d"]
data.drop(drop_list,axis=1,inplace=True)

#创建一个vacancy 类型，填充缺失值
objectcolumns=[i for i in data.columns if data[i].dtype=="object"]
data[objectcolumns]=data[objectcolumns].fillna("vacanct")

import missingno as msno   # 缺失值可视化
msno.matrix(data[objectcolumns])

#查看float数据类型缺失情况
floatcolumns=[i for i in data.columns if data[i].dtype=="float"]
data[floatcolumns].isnull().sum().sort_values(ascending=False)

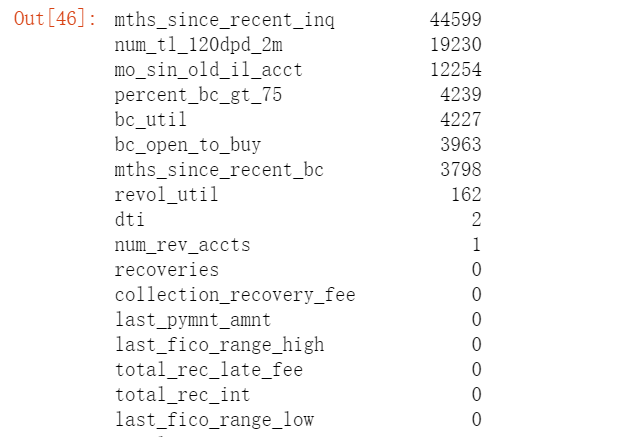
对于数值型数据我们先采用均值填补

from sklearn.preprocessing import Imputer
imp = Imputer(missing_values=np.nan , strategy='mean',copy=False, axis=0)
imp=imp.fit(data[floatcolumns])
data[floatcolumns]=imp.transform(data[floatcolumns])

 

 极端值这里暂时不做处理，因为是做评分卡，后续会做分箱操作

对object数据再次进行数据过滤，看看是否需要筛选

objectColumns = [i for i in data.columns if data[i].dtype=="object"]
var = data[objectColumns].columns
for v in var:
    print('\nFrequency count for variable {0}'.format(v))
    print(data[v].value_counts())

data_drop=data[["sub_grade","pymnt_plan","title","last_pymnt_d","last_pymnt_d","last_credit_pull_d","application_type","hardship_flag",
              "debt_settlement_flag"]]
data=data.drop(data_drop,axis=1)

  2.特征抽象

  这里我们优先使用类别标签，暂时不用哑变量，后续看模型效果也可以尝试哑变量

data_list={
    "grade":{"A":1,"B":2,"C":3,"D":4,"E":5,"F":6,"G":7},
    "emp_length":{"10+ years":11,"2 years":2,"< 1 year":0,"3 years":3,"1 year":1,"5 years":5,"4 years":6,"vacanct":0,
                  "8 years":8,"7 years":7,"6 years":6,"9 years":9 },
    "home_ownership":{"MORTGAGE":1,"RENT":2,"OWN":3,"ANY":4 },
    "verification_status":{"Source Verified":1,"Verified":2,"Not Verified":3},
    "loan_status":{'Current':0,'Fully Paid':0,'Charged Off':1,'Late (31-120 days)':1,'Late (16-30 days)':1,'In Grace Period':1,"Default":1},
    "purpose":{"debt_consolidation":1,"credit_card":2,"home_improvement":3,"other":4,"major_purchase":5,"medical":6,"car":7,
               "small_business":8,"moving":9,"vacation":10,"house":11,"renewable_energy":12,"wedding":13,"educational":14},
    "initial_list_status":{"w":1,"f":2},
    "term":{36.0:1,60.0:2}
}
data=data.replace(data_list)#映射

n_columns = ["home_ownership","verification_status","purpose","application_type"] 
dummy_df = pd.get_dummies(data[n_columns])# 用get_dummies进行one hot编码
loans = pd.concat([data, dummy_df], axis=1) #当axis = 1的时候，concat就是行对齐，然后将不同列名称的两张表合并
data = data.drop(n_columns, axis=1)  #清除原来的分类变量

同值信息处理

from scipy.stats import mode
equ_fea=[]
for i in data1.columns:
        mode_value=mode(data1[i])[0][0]
        mode_rate=mode(data1[i])[1][0]/data1.shape[0]
        if mode_rate >0.9:
            equ_fea.append([i,mode_value,mode_rate])
dt=pd.DataFrame(equ_fea,columns=["name","value","equi"])
dt.sort_values(by="equi")

 再剔除信息泄露属性

drop_data_leakage=data[["recoveries","last_pymnt_amnt","funded_amnt","funded_amnt_inv","total_pymnt","total_pymnt_inv","total_rec_prncp",
                  "total_rec_int"]]
a=data.drop(drop_data_leakage,axis=1,inplace=True)

特征衍生

#我们呢把'annual_inc'年收入/12 得到客户月收入，然后在用"installment" 除以月收入得到得到每月还款与月收入的比，值越大客户还款压力越大
data["installment_feat"]=data["installment"] / (data["annual_inc"]/12)

#把时序变量变成月份值，用借款发放时间 - 首次使用信用卡时间，作为一个新变量，表示信用历史
a=(data["issue_d"]-data["earliest_cr_line"])/30
data["cre_hist"]=a
data.drop(["issue_d","earliest_cr_line"],axis=1,inplace=True)

data.to_csv("2017q1_2.csv",index=False)

连续变量分箱：

      分箱方法包括有监督的 卡方分箱 KS分箱和决策树分箱，无监督的 等宽 等频等分箱

     一开始打算采用卡方分箱，但是有的数据莫名其妙出错，要么就跑一晚上没有反应，以为是正太分布的问题，半天也没有解决，最后改用决策树分箱。

def Chi2(df, total_col, bad_col,overallRate):
    '''
     #此函数计算卡方值
     :df dataFrame
     :total_col 每个值得总数量
     :bad_col 每个值的坏数据数量
     :overallRate 坏数据的占比
     : return 卡方值
    '''
    df2=df.copy()
    df2['expected']=df[total_col].apply(lambda x: x*overallRate)
    combined=zip(df2['expected'], df2[bad_col])
    chi=[(i[0]-i[1])**2/i[0] for i in combined]
    chi2=sum(chi)
    return chi2
#最大分箱数分箱
def ChiMerge_MaxInterval_Original(df, col, target,max_interval=5):
    '''
    : df dataframe
    : col 要被分项的特征
    ： target 目标值 0,1 值 1 为反  0 为正
    : max_interval 最大箱数
    ：return 箱体
    '''
    colLevels=set(df[col])
    colLevels=sorted(list(colLevels))
    N_distinct=len(colLevels)
    if N_distinct <= max_interval:
        print ("the row is cann't be less than interval numbers")
        return colLevels[:-1]
    else:
        total=df.groupby([col])[target].count()
        total=pd.DataFrame({'total':total})
        bad=df.groupby([col])[target].sum()
        bad=pd.DataFrame({'bad':bad})
        regroup=total.merge(bad, left_index=True, right_index=True, how='left')
        regroup.reset_index(level=0, inplace=True)
        N=sum(regroup['total'])
        B=sum(regroup['bad'])
        overallRate=B*1.0/N
        groupIntervals=[[i] for i in colLevels]
        groupNum=len(groupIntervals)
        while(len(groupIntervals)>max_interval):
            chisqList=[]
            for interval in groupIntervals:
                df2=regroup.loc[regroup[col].isin(interval)]
                chisq=Chi2(df2,'total','bad',overallRate)
                chisqList.append(chisq)
            min_position=chisqList.index(min(chisqList))
            if min_position==0:
                combinedPosition=1
            elif min_position==groupNum-1:
                combinedPosition=min_position-1
            else:
                if chisqList[min_position-1]<=chisqList[min_position + 1]:
                    combinedPosition=min_position-1
                else:
                    combinedPosition=min_position+1
            #合并箱体
            groupIntervals[min_position]=groupIntervals[min_position]+groupIntervals[combinedPosition]
            groupIntervals.remove(groupIntervals[combinedPosition])
            groupNum=len(groupIntervals)
        groupIntervals=[sorted(i) for i in groupIntervals]
        print (groupIntervals)
        cutOffPoints=[i[-1] for i in groupIntervals[:-1]]
        return cutOffPoints
#返回最佳切分点array

import numpy as np
from scipy.stats import kstest
kstest(b, 'norm')  #正太分布检验  p值大于0.05 表示符合正太分布

#先切分下需要分箱的数据
x_data=data["open_acc"]
x1_data=x_data[:,np.newaxis] #sklearn要求x，至少是二维数据，所以需要增加一维，np.newaxis 的位置决定了增加维度的位置
x1_data

#做单变量决策树
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier( max_depth=3,min_samples_leaf=21054).fit(x1_data,data["loan_status"])

#显示图形
from sklearn import tree
import graphviz
dot_data = tree.export_graphviz(model, out_file=None)
graphviz.Source(dot_data)

略过图形展示

#通过决策树得到所有切分点，并转换成字典
num_box=["loan_amnt","int_rate","dti","fico_range_low","installment","annual_inc","fico_range_high","open_acc"]
cut_list=[
    [4012,5987,7012,9012,10012,19987,20012,23987,28112],
    [6.905,8.045,10.565,11.76,12.49,13.665,15.88,17.915,19.94],
    [7.445,10.075,12.625,14.855,20.195,21.795,25.135,30.115,34.275],
    [667.5,677,683,687,692,697,707,727,747],
    [161,197,251,503,602,880],
    [42800,55101,65732,85085,104499,120287,150486],
    [671.5,686.5,691.5,701.5,711.5,731.5,751.5],
    [5.5,7.5,8.5,10.5,17.5,22.5]]
cut_dict={}
for i in range(len(num_box)):
    cut_dict[num_box[i]]=cut_list[i]

#采用pd.cut()划分数据
def box_col_to_df(to_box,col,num_b):#数据集    需要转换的数据列   切割点LISI
    bins=[-100.0]+num_b+[1000000000.0] #因为pd.cun()是封闭的，这里把bins的上下区间扩大
    to_box[col]=pd.cut(to_box[col],bins=bins,include_lowest=True,labels=range(len(bins)-1))

box_col_to_df(data,"open_acc",cut_dict["open_acc"])

完成后的数据如下

 

用随机森林对变量重要程度排序

已经提前切分了 X与 y

from sklearn.ensemble import RandomForestClassifier
clf=RandomForestClassifier().fit(x,y)

一开始这里出现错误，显示 x存在 空值或者无穷大

 #找到无穷值
inf_list= np.isinf(data).sum().tolist()#把每一列的无穷值个数加起来
sum(inf_list)#如果sum(nan_inf) 为0，则不存在无穷值；如果不为0，则存在。

#定位无穷值
abnormal_index = [ [inf_list.index(i)] for i in inf_list if i != 0 ]#遍历列表，找到所有非0值的索引。
print(data.columns[abnormal_index])

 只有2个，所以删除相应行就可以了

再跑一次随机森林

然后输出变量重要程度

#输出变量重要程度排序
importance = clf.feature_importances_
indices = np.argsort(importance)[::-1]
features = x.columns
name=[]
degree=[]
for f in range(x.shape[1]):
    name.append(features[f])
    degree.append(importance[indices[f]])
zy=pd.DataFrame({"name":name,"degree":degree})
print(zy)

 

 先截取前15个变量看效果

degree_list=df.loc[:15,"name"]
df=data[degree_list]

 计算woe值与IV值

#封装woe与IV值计算函数
def Calcwoe(data,col,target):
    total=data.groupby([col])[target].count()
    total=pd.DataFrame({"total":total})
    bad=data.groupby([col])[target].sum()
    bad=pd.DataFrame({"bad":bad})
    regroup=total.merge(bad,left_index=True,right_index=True,how="left")
    regroup.reset_index(level=0,inplace=True)
    n=sum(regroup["total"])
    b=sum(regroup["bad"])
    regroup["good"]=regroup["total"]-regroup["bad"]
    g=n-b
    regroup["bad_pcnt"]=regroup["bad"].map(lambda x: x*1.0/b)
    regroup["good_pcnt"]=regroup["good"].map(lambda x : x*1.0/g)
    regroup["woe"]=regroup.apply(lambda x: np.log(x.good_pcnt*1.0/x.bad_pcnt),axis=1)
    woe_dict=regroup[[col,"woe"]].set_index(col).to_dict()
    IV=regroup.apply(lambda x:(x.good_pcnt-x.bad_pcnt)*np.log(x.good_pcnt*1.0/x.bad_pcnt),axis=1)
    IV_SUM=sum(IV)
    return {"woe":woe_dict,"IV_SUM":IV_SUM,"IV":IV}

计算IV值
df=data.copy()
woe_dist={}
IV_list=[]
for i in df.columns:
    iv_dict=Calcwoe(df,i,"loan_status")
    IV_list.append(iv_dict["IV_SUM"])
    woe_dist[i]=iv_dist["woe"]
DF_IV=pd.DataFrame({"iv_name":df.columns.values,"IV":IV_list})
DF_IV.sort_values(by="IV",ascending=False)

 iv值出现（无穷大）表明 特征中的某些属性缺失 某一类样本，这种情况下需要从新分箱，合并属性

 

 

 再次查看IV值

计算IV值
df=data.copy()
woe_dist={}
IV_list=[]
for i in df.columns:
    iv_dict=Calcwoe(df,i,"loan_status")
    IV_list.append(iv_dict["IV_SUM"])
    woe_dist[i]=iv_dist["woe"]
DF_IV=pd.DataFrame({"iv_name":df.columns.values,"IV":IV_list})
DF_IV.sort_values(by="IV",ascending=False)

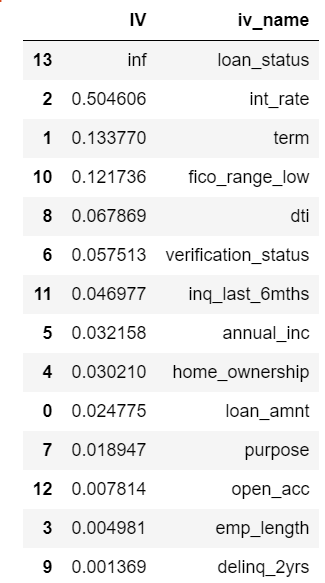
之后可以保留IV值大于0.015变量，也可以保留大于0.02的变量，看实际情况

 下面利VIF（方差膨胀系数）检验多重共线性，既用其他特征拟合这一特征，如果解释性很强，说明他们存在共线性

#利用VIF（方差膨胀系数）检验多重共线性
from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF
VIF_ls=[]
n=df.columns
for i in range(len(n)):
    VIF_ls.append([n[i],int(VIF(df.values,i))])
df_vif=pd.DataFrame(VIF_ls,columns=["name","vif"])
print(df_vif)

#利用协方差计算线性相关性
cor=data[num_box].corr()
cor.iloc[:,:]=np.tril(cor.values,k=-1)
cor=cor.stack()
cor[np.abs(cor)>0.7]

# VIF 大于 10 cor 大于0.7 变量之间存在相关性    这里我们逐一删除，如当删除 installment 之后，vif小于10，那么installment和 loan_amnt
#选择iv值大的哪一个
df.drop("fico_range_high",axis=1,inplace=True )
df.drop("installment",axis=1,inplace=True)
df.drop("grade",axis=1,inplace=True)

valid_feas=DF_IV[DF_IV.IV > 0.015].iv_name.tolist()
valid_feas

df=df[valid_feas]
df.head()

#用热力图看看相关性
colormap = plt.cm.viridis
plt.figure(figsize=(12,12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(df.corr(),linewidths=0.1,vmax=1.0, square=True, cmap=colormap, linecolor='white', annot=True)

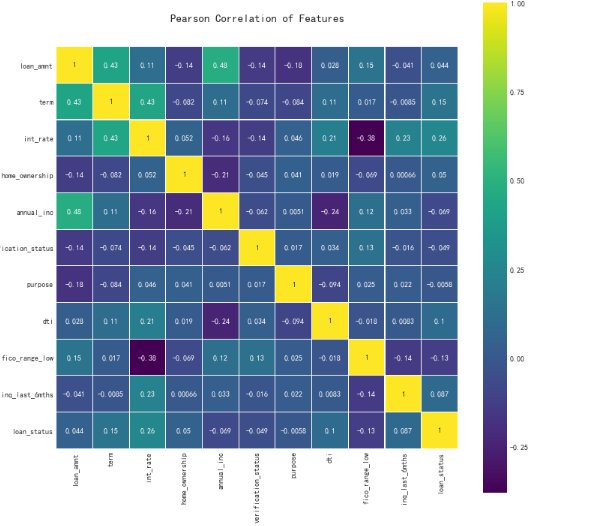
 解决样本不均衡问题，方法有，过采样，和欠采样，以及有放回随机抽样等方法，本次采用过采样平衡正反样本。

#利用过采样方法，解决样本不均衡问题
#划分x和y
x_list=list(df.columns)
x_list.remove("loan_status") #再x_list中剔除 loan_status 变量
x=df[x_list]
y=df["loan_status"]

n_sample=y.shape[0]
n_pos_sample=y[y==0].shape[0]
n_neg_sample=y[y==1].shape[0]
print("样本个数:{},正样本占比:{:.2%},负样本占比:{:.2%}".format(n_sample,
                                         n_pos_sample/n_sample,
                                        n_neg_sample/n_sample))

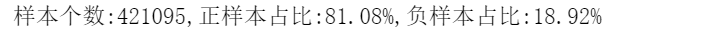
from imblearn.over_sampling import SMOTE # 导入SMOTE算法模块
# 处理不平衡数据
sm = SMOTE(random_state=42)    # 处理过采样的方法
x, y = sm.fit_sample(x, y)
print('通过SMOTE方法平衡正负样本后')
n_sample = y.shape[0]
n_pos_sample = y[y == 0].shape[0]
n_neg_sample = y[y == 1].shape[0]
print('样本个数：{}; 正样本占{:.2%}; 负样本占{:.2%}'.format(n_sample,
                                                   n_pos_sample / n_sample,
                                                   n_neg_sample / n_sample))

df.to_csv("2017q1_df.csv",index=False)

# 用woe编码替换原属性值，这样可以让系数正则化
for i in range(len(x.columns)):
    x[x.columns[i]].replace(woe_dict[x.columns[i]],inplace=True)

开始训练模型

#x增加一列全为1，得到方程截距
import statsmodels.api as sm
x1=sm.add_constant(x_train)

x_train,x_text,y_train,y_test=train_test_split(x1,y,test_size=0.2,random_state=1991)# 切分比列为2-8，切分，并设置随机数种子

#利用交叉验证和网格搜索
from sklearn.model_selection import GridSearchCV  #网格搜索
from sklearn.linear_model import LogisticRegression # 逻辑回归
from sklearn.model_selection import train_test_split # 测试集与训练集划分

#构建网格参数组合
param_test1={"C":[0.01,0.1,1.0,10.0,20.0,30.0,100.0,200.0,300.0,1000.0], #正则化系数
            "penalty":["l1","l2"] #正则化参数
            "max_iter":[100,200,300,400,500]} #算法收敛的最大迭代次数
gsearch1=GridSearchCV(LogisticRegression(),param_grid=param_test1,cv=10)
gsearch1.fit(x_train,y_train)  #训练模型

gsearch1.best_params_, gsearch1.best_score_   #查看评分最高的参数组合与最佳评分

gsearch1.best_estimator_  # 最佳参数分类器

 

 利用网格搜索得到的最佳参数训练模型

from sklearn.linear_model import LogisticRegression
flt= LogisticRegression(penalty='l2',C=0.01)
flt.fit(x_train,y_train)

 用验证集查看模型效果

auc=roc_auc_score(flt.predict(x_text),y_test)
fpr,tpr,thre=roc_curve(flt.predict(x_text),y_test)
ks=max(tpr-fpr)
print("auc:{}       ks:{}".format(auc,ks))

#查看准确率
from sklearn.metrics import accuracy_score
print("准确率:{:.4%}".format(accuracy_score(flt.predict(x_text),y_test)))

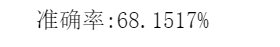
flt.coef_ #查看系数

 ks值大于0.3说明是一个基本能用的模型

输出评分卡：

#输出评分卡
#假设比率为1/20 时 分值是500，比率每翻倍一次的20分
B=20/np.log(2) 
A=500+B*np.log(1/20)
basescore=round(A-B*flt.coef_[0][0],0) #基准分四舍五入取整
scorecard={}
for i,j in enumerate(x.columns):
    woe=woe_dict[j]["woe"]
    interval=[]
    scores=[]
    for key,value in woe.items():
        score=round(-(value*flt.coef_[0][i+1]*B))
        scores.append(score)
        interval.append(key)
    data=(pd.DataFrame({"interval":interval,"scores":scores})).set_index("interval").to_dict()
    scorecard[j]=data
print(scorecard)

 

 整理之后得到评分卡。

  得到评分卡之后我们通常需要计算出最佳的分数切割点，可以用ROC曲线，找到拐点的值，带入评分卡方程就是我们的最佳切割分数

  也可以利用，卡方分箱，或者决策树，将评分分箱，计算每一箱的逾期率，根据业务情况选择切割分数。

总结

 

1.每一种方法没有好坏的区分，只有适合与不适合，更多时候我们需要都用一边，才知道某一种算法适合什么数据。

2.制作模型本身是一个不断迭代寻找最优的过程，当我们构建出一个模型之后如果效果不理想，那么需要我们从数据清洗开始从新来做，比如缺失       值填充是用均值还是众数？分类变量使用 标签法，还是做哑变量呢，这些我们都要一一尝试不断迭代，得到我们的最终模型。

3.变量选择 很重要，人们常说数据决定的模型的顶点，而算法用于逼近顶点，可见再特征选择上我们要尽量的贴合业务实际情况，要想得到好的模     型最终还是要在数据上下功夫，这说明数据清洗与准备过程，再整个建模流程中是比较重要的。

 参考：

 https://zhuanlan.zhihu.com/p/39780207

https://blog.csdn.net/zs15321583801/article/details/89485951