机器学习常用算法与辅助函数公式

1.去量纲

   标准化：x=(x-min(x))/(max(x)-min(x))   特点：容易受极端值影响，需要先去除极端值。

 归一化：z-score=（x-均值）/标准差      特点：不受极端值影响，但是计算量较大

2.辅助函数

  Sigmoid函数：  1 / （1+e^-x）发生的概率   1 / （1-e^-x）不发生的概率      

  证据权重(WOE值)：    woe(x_i)=ln（B₁/B_总)/(G₁/G总)   其中: x=某一特征  B₁₌x特征中好客户中的一组的样本数 G₁₌x特征中坏客户中的   一组的样本数，

  信息价值（IV值):     IV_i= （B₁/B_总)-(G₁/G总) * woe(x_i)   而得到每一组的IV值之后，所有IV值相加就得到整个变量X的IV值。

                       特点：再公式中B₁或者G_1，任一组样本数不能为0，否者 IV值=-∞  或者 ∞  变得毫无意义。

                       注：一般数值越大表明越不会干什么，该值放在分子位置上，如分子位是未逾期客户，则数值越大越不会逾期。

                       一般情况下：无预测能力←0.03←低→0.09←中→0.29←高→0.49→极高

  方差膨胀因子(VIF):    VIF_{i = 1 / 1-R²}      用于多重共线性检验，假设有（x1x2x3...xn)个自变量，R² =所有变量对X_i变量做线性回归所得的R²，以此类推，计算所有变量的VIF，一般要求VIF<10,如果变量较少也可以要求<5，大于这个数说明存在多重共线性，需要将VIF 大于10的变量依次剔除，再次计算VIF，当发现剔除X_k个变量之后VIF小于10，那么X_i 与 X_k 可选择IV值 较高的一个进行保留。

 

---

   3.模型方程

最小二乘矩阵方程：（求回归）

                       W=(X^T*X)^-1* X^T *Y         其中：X^T 表示转置    (X^T*X)^-1  表示逆矩阵    

     岭回归矩阵方程：   

                        w=(X^T * X+aI)^-1 * X^T* Y   其中 a是⾃定义参数， I则是单位矩阵

     梯度下降矩阵方程：

                         θ=θ-σX^T(X*θ-Y) / m  其中 θ 为假设系数  σ为学习率（步长）

    梯度下降逻辑回归：

                        θ=θ-σX^T(Sigmoid*(X*θ)-Y) / m

 

---

 

评分卡计算方程：     odds为good用户概率（p）与bad用户概率（1-p）的比值，=odds = p/1-p

                        评分卡设定的分值刻度可以通过将分值表示为比率对数的现行表达式来定义。公式如下：

                            score总=A+B∗ln(odds)

              反过来：      odds为bad用户概率（p）与good用户概率（1-p）的比值，= odds = p/1-p

                那么：      score总=A-B∗ln(odds)

    以第二个方程为例：      其中，A和B是常数。式中的负号可以使得违约概率越低，得分越高。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低 分值代表高风险。 逻辑回归模型计算比率如下所示：

                                               

                                                 Ln(p/(1-p)) =β₀ +β₁*x₁ +β₂*x₂ +β₃*x₃ +...+β_n*x_n

                                                 其中，用建模参数拟合模型可以得到模型参数β0，β1，…，βn。

                            式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。

     注：odds: 称为几率、比值、比数，是指某事件发生的可能性(概率)与不发生的可能性（概率）之比。用p表示事件发生的概率，则：odds = p/(1-p)

                     由上式可得，  p(y=1) = e^z/(1+e^z) 

                                   p(y=0) = 1/(1+e^z) 

                                 p为事件发生概率           

     首先我们需要设定两个假设：

     (1）给某个特定的比率设定特定的预期分值；

      2）确定比率翻番的分数（PDO） 根据以上的分析，我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值为P+PDO。   代入式中，可以得到如下两个等式：

                                    

                             解上述两个方程中的常数 A 和 B, 可以得到：

                                           B=PDO/log(2)

                        A=P+Blog(x)

                         假设 设定评分卡刻度使得比率为x={1:20}（违约正常比）时的分值为50分，PDO为10分，代入式中求得：B=14.43，A=6.78 则分值的计算    式可表示为：

                                  

                             评分卡刻度参数A和B确定以后，就可以计算比率和违约概率，以及对应的分值了。通常将常数A称为补偿，常数B称为刻度。 则评分卡的分值可表达为：

                               

                             如果x1…xn变量取不同行并计算其WOE值，式中表示的标准评分卡格式，基础分值等于(A−Bβ0)；由于分值分配公式中的负号，模型参数β0，β1，…，βn也应该是负值；变量xi的第j行的分值取决于以下三个数值：

                                                      

在求得得分之后通常我们需要计算一个最佳的切割点，得到最佳分值

方法1：参照ROC曲线作图，计算样本发生概率=x ，灵敏度*（1-（1-特异度））=y ，作图x轴等于x ， y 轴等于y， 通常情况下拐点对应的x，即为最佳切割点，将该点x值代入方程，得到最佳切割分数。

方法2：将结果降序排序并10等分，分别计算每一份的逾期概率，之后根据业务需要，手动划分切分分数

---

决策树方法：

    1. 信息增益     ID3

            信息熵：

                  信息熵是度量样本集合纯度最常用的一种指标，假设：样本集合D中第K类样本所占的比列为pk，则D的信息熵为

                           Ent(D）= - Σ ^|y|(pk*log₂(pk))     Ent(D）的值越小，则D 的纯度越高，|y|等于分类个数

                     注：log₂(pk） 表示 以2为底，取pk'的对数

                         如果pk=0 那么pk log₂pk=0

                         Ent(D）最小值为0  最大值为log₂|y|

       信息增益：

               Gain（D,a）=Ent(D)-Σ^v（|D^u| /|D| *Ent(D)）

            其中：D 为数据集    a 为数据集中的一个属性    v 表示a属性可能的取值个数

                  D^u 表示第u个分支点包含了D中所有在属性a 上取值为a^u 的样本

             一般，信息增益越大，意味着使用属性a 来进行划分所获得的纯度提升越大，因此我们可以以信息增益为准则来选择划分属性：      a_* = arg max Gain（D，a）

     以西瓜书 西瓜数据集2.0 为列：

      

 

 

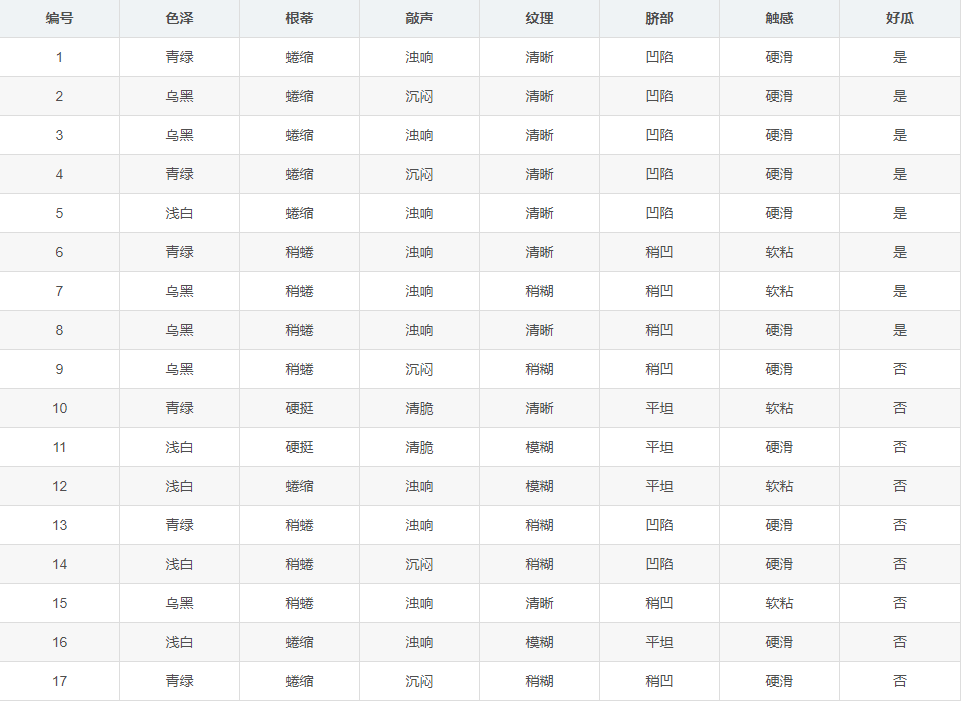
 表中一共又17个样列，|y|=2   根节点包含D中所有的样列，其中正列 占比 p1=8/17     反列占比p2 = 9/17，于是可算出信息熵（D）等于

                           Ent（D）=-Σ²pk*log₂(pk )=-（8/17 *log₂ (8/17)   + 9/17 * log₂ (9/17)）=0.998

然后计算各个属性的信息增益，以色泽为列：

                       色泽属性又三个取值（青绿，乌黑，浅白）使用该属性对D进行划分，则我们可得到三个子集 D¹ ,D² ,D³,分别对应 青绿，乌黑，浅白，其中D¹中包含编号为（1，4，6，10，13，17）的6个样列，其中正列 p1 = 3/6   反列 p2 =3/6，D^2,D^3,,同理，因此我们可以计算出按照 色泽 划分后 所获得的三个分支节点的信息熵如下：

 

                        、Ent(D¹)=-(3/6 *log₂ (3/6) + 3/6log₂ (3/6)) =1.000   (青绿)

                          Ent(D²)=-(4/6 *log₂ (4/6) + 2/6*log₂ (2/6)) =0.918   (乌黑)

                          Ent(D³)=-(1/5 *log₂ (1/5) + 4/5*log₂ (4/5)) =0.722    (浅白)

  又： 根据信息增益公式，计算出 色泽 的信息增益等于

                           Gain（D,色泽）=Ent(D)-Σ³（|D^u| /|D| *Ent(D)）

                                          = 0.998 - （6/17 *1.000 + 6/17 * 0.918 + 5/17 * 0.722）

                                          = 0.109

同理得到：      Gain（D,跟蒂）=  0.143         Gain（D,敲声）=    0.141         Gain（D,纹理）= 0.381

                        Gain（D,脐部）=   0.289       Gain（D,触感）=  0.006

                      其中纹理的信息增益最大，于是他被选为划分属性，那么基于  纹理 对根节点进行划分的结果为

                                      清晰    （ 1，2，3，4，5，6，8，10，15）

                          纹理     稍糊     （7，9，13，14，17）

                                      模糊       （11，12，16）

                    接下来以（纹理=清晰）为列，继续划分：

                      首先是脐部：清晰共包含9个样例，其中 正列=7/9    反列 =2/9   

                               Ent（D)= -(7/9*log₂(7/9)+2/9*log₂(2/9)

                                            =0.764

                               Ent(D¹)= -(1*log₂(1)+0=0       （凹陷）

                               Ent(D²)= -(2/3*log₂(2/3)+1/3*log₂(1/3) = 0.918      （稍凹）

                               Ent(D³)=-(0+1*log₂(1))=0    （平坦)

                   随意脐部的信息增益= Dain（D¹,脐部)=0.764-(0.918*3/9)

                                                      = 0.764-0.306

                                                      =  0.458

                                同理可得：  Dain（D¹,色泽)  =  0.043    Dain（D¹,根蒂)   =  0.485    Dain（D¹,敲声)   =   0.331    

Dain（D¹,触感) =   0.485 

                     有三个属性获得最大信息增益，任选其一作为划分，以此类推，对所有分支节点进行以上操作，最终得到决策树.

---

 

增益率  C4.5算法

                        信息增益算法会可取值数目较多的属性有所偏好，而C4.5用于减少这种偏好带来的不利影响，公式为：

                                     Dain_ratio(D,a)=  Gain(D,a)   /   IV(a)

                     其中：

                                   IV(a)= -Σ^v（|D^V| /  |D|  *  log2(|D^V|  /  |D| )

                      注明：属性a 可取值的数目越多（即V 越大）IV(a) 的值就越大，另外增益率对可取值数目较少的属性有所偏好，所以C4.5不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：

                                   即 先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

---

基尼系数：（Gini）

                       CART树采用基尼系数来选择属性划分，数据集D的纯度可用基尼系数来度量：

                                                 Gini(D)=∑^|y|∑_k´≠k pk pk´

                                                        =  1- ∑^|y| p² k

                         Gini(D) 反应了从数据集D中随机抽取两个样本，其类别标记不一致的概率，所以，Gini(D）越小，则数据集D 的纯度越高，

                         属性a 的基尼系数定义为：

                                                 Gini_index(D,a)=∑^v (|D^v| / |D|  *  Gini(D^v)）

剪枝策略：

                        预剪枝：基于贪心本质禁止这些分支展开，给决策树带来了欠拟合风险。

                         后剪枝：欠拟合风险很小，泛化性能由于预剪枝，但是后剪枝过程是在生成决策树之后进行的，并且要自下向上的对树中的所有非叶节点进行逐一考察，因此训练时间开销要比未剪枝决策树和预剪枝决策树都要大很多。

                          详细内容参考：机器学习(周志华） 第四章 第三 节

---

 

4.模型稳定性检测指标 (PSI)：

                     群体稳定性指标：

                                     假设我们用logistic回归模型建立了一个模型，那么我的训练集会输出一个结果 A  ,放入测试集我的模型也会输出一个结果B,然后将A排序之后10等分（等宽分组），计算每组中每个预测类的占比，记作预期占比，然后按照 A十等分之后每组的上下限为界限，将B也分成10份，不一定是等分的，计算个组中类的占比，记作 实际占比，意义在于如果模型更稳定，那么在新的数据上预测所得类概率应该和建模分布一致，这样落在建模数据集所得的类概率所划分的等分区间上的样本占比应该和建模时一样，否则说明模型变化，一般来自预测变量结构变化，通常用作模型效果监测。

                                                PSI=sum(（实际占比-预期占比）* ln(实际占比/预期占比)) 

                   数据分布稳定性：

                                     现有数据记作A     建模数据记作 B

                                                PSI= sum(（样本A分布占比-样本B分布占比）* ln(样本A分布占比/样本B分布占比))

                                              一般我们认为：    稳定←0.1←一般→0.25→重构模型