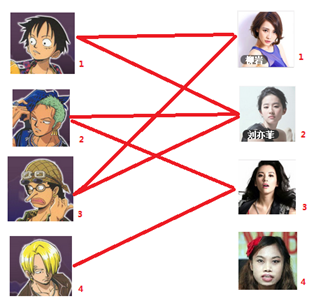
先通过一个有趣的例子了解一下二分图的大致意思:
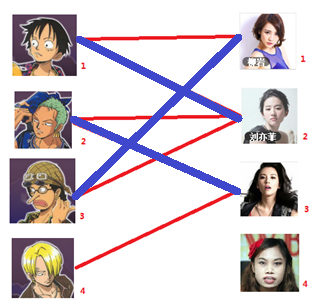
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感( -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
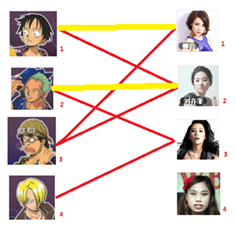
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================================
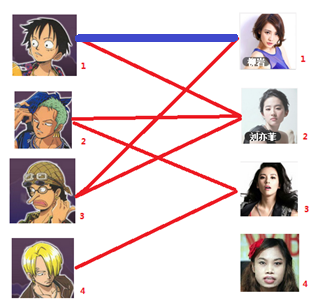
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
===============================================================================
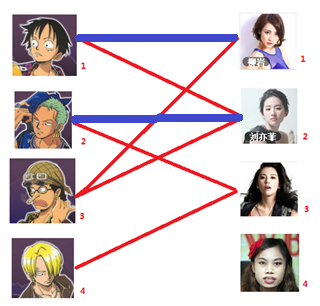
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
===============================================================================
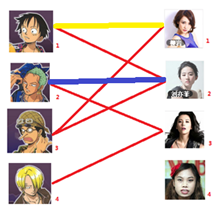
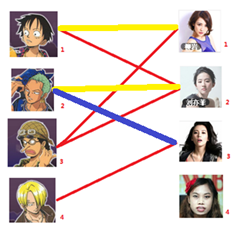
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
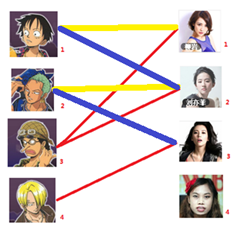
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配(
 )重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
)重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
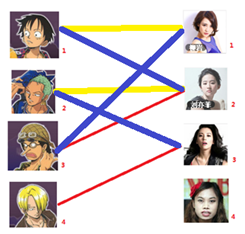
所以第三步最后的结果就是:
===============================================================================
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================================
其原则大概是:有机会上,没机会创造机会也要上
基本概念—二分图
1 二分图
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y,并且图中每条边连接的两个顶点一个在X中,另一个在Y中,则称图G为二分图。
2 匹配
M包含于E(G),任意ei,ej∈M,ei,ej不存在公共顶点,则M是图G的一个匹配。
M中的每个端点称为被M匹配。
3 完美匹配
G中的每个顶点都被M匹配了,则称M是G的一个完美匹配。
4 匹配的大小
M中边的条数,记为|M|
5 极大匹配
每次选择一条边使得其端点没有被已经选出的边用过,直到没有可选的边为止。(极大匹配不是最大匹配)
6 交错路径和增广路径
如果一条路径的边交替出现在M中和不出现在M中,则称这条路径为一条M-交错路径。
路径的起始点和终点未被M匹配的M-交错路径称为M-增广路径。
7 berge定理
对称差:A△B=(A-B)∪(B-A)
G=(V,E)的任意两个匹配M,M'的对称差,其分量或者是一条路径,或者是一个偶环。
berge定理:M是G的最大匹配,当且仅当G中不存在M-增广路径。
匈牙利算法
(具体思想看上面找女朋友的例子,这个是匈牙利算法的DFS表现)
#define maxn 10//表示x集合和y集合中顶点的最大个数! int nx,ny;//x集合和y集合中顶点的个数 int edge[maxn][maxn];//edge[i][j]为1表示ij可以匹配 int cx[maxn],cy[maxn];//用来记录x集合中匹配的y元素是哪个! int visited[maxn];//用来记录该顶点是否被访问过! int path(int u) { int v; for(v=0;v<ny;v++) { if(edge[u][v]&&!visited[v]) { visited[v]=1; if(cy[v]==-1||path(cy[v]))//如果y集合中的v元素没有匹配或者是v已经匹配,但是从cy[v]中能够找到一条增广路 { cx[u]=v; cy[v]=u; return 1; } } } return 0; } int maxmatch() { int res=0; memset(cx,0xff,sizeof(cx));//初始值为-1表示两个集合中都没有匹配的元素! memset(cy,0xff,sizeof(cy)); for(int i=0;i<=nx;i++) { if(cx[i]==-1) { memset(visited,0,sizeof(visitited)); res+=path(i); } } return res; }
时间复杂度:匈牙利算法每次寻找增广路径的时间复杂度是O(m) 最多需要寻找O(n)次,所以复杂度是O(nm)
Hopcroft-Karp算法
该算法由John.E.Hopcroft和Richard M.Karp于1973提出,故称Hopcroft-Karp算法。
原理
为了降低时间复杂度,可以在增广匹配集合M时,每次寻找多条增广路径。这样就可以进一步降低时间复杂度,可以证明,算法的时间复杂度可以到达O(n^0.5*m),虽然优化不了多少,但在实际应用时,效果还是很明显的。
/**dx[i]表示左集合i顶点的距离编号,dy[i]表示右集合i顶点的距离编号**/ /**mx[i]表示左集合顶点所匹配的右集合顶点序号,my[i]表示右集合i顶点匹配到的左集合顶点序号。**/ struct edge { int v,next; }e[Mm]; int tot,head[Mn]; void addedge(int u,int v) { e[tot].v=v; e[tot].next=head[u]; head[u]=tot++; } int mx[Mn],my[Mn],vis[Mn]; int dis; int dx[Mn],dy[Mn]; int n,m; bool searchp() { queue<int>q; dis=INF; CLR(dx,-1); CLR(dy,-1); for(int i=1;i<=n;i++) { if(mx[i]==-1) { q.push(i); dx[i]=0; } } while(!q.empty()) { int u=q.front(); q.pop(); if(dx[u]>dis) break; for(int i=head[u];~i;i=e[i].next) { int v=e[i].v; if(dy[v]==-1) { dy[v]=dx[u]+1; if(my[v]==-1) dis=dy[v]; else { dx[my[v]]=dy[v]+1; q.push(my[v]); } } } } return dis!=INF; } bool dfs(int u) { for(int i=head[u];~i;i=e[i].next) { int v=e[i].v; if(vis[v]||(dy[v]!=dx[u]+1)) continue; vis[v]=1; if(my[v]!=-1&&dy[v]==dis) continue; if(my[v]==-1||dfs(my[v])) { my[v]=u; mx[u]=v; return true; } } return false; } int maxMatch() { int res = 0; CLR(mx,-1); CLR(my,-1); while(searchp()) { CLR(vis,0); for(int i=1;i<=n; i++) if(mx[i] == -1 && dfs(i)) res++; } return res; } void init() { tot=0; CLR(head,-1); }
参考博文:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号