ABC257G

设 $f(S)$ 表示将字符串 $S$ 拆分成 $T$ 的前缀相连，最少需要划分成几段。

需要注意到一个性质，每个字符串被拆分时，最后一个子串应尽可能长。换句话说，若字符串 $A,B$ 都是可以转移的位置，且 $A$ 是 $B$ 的前缀，则必有 $f(A)\lt f(B)$，从 $A$ 转移一定最优。

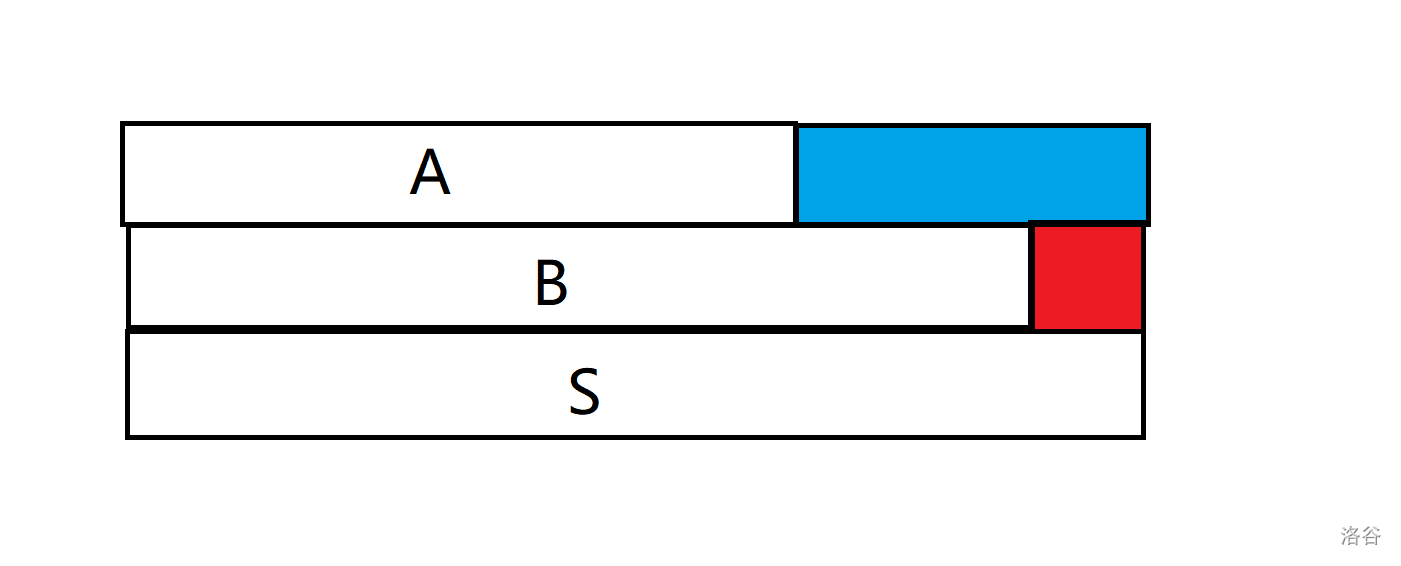
蓝色的部分和红色的部分都是 $T$ 的前缀，若 $f(A)\ge f(B)$，那么不难发现蓝色的部分减去红色的部分一定也是 $T$ 的前缀，那么 $f(B)$ 减去这一段就是 $f(A)$ 的可能值，即 $f(A)\le f(B)-1\Longleftrightarrow f(A)\lt f(B)$。

于是直接上一个 KMP 就好了。

注意中途如果匹配不上了就直接输出 -1。

Code：

#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
int n, m;
char a[N], b[N];
int nxt[N], f[N];

int main() {
	scanf("%s%s", a + 1, b + 1);
	n = strlen(a + 1), m = strlen(b + 1);
	nxt[1] = 0;
	for (int i = 2, j = 0; i <= n; ++i) {
		while (j > 0 && a[i] != a[j + 1]) j = nxt[j];
		if (a[i] == a[j + 1]) ++j;
		nxt[i] = j;
	}
	for (int i = 1, j = 0; i <= m; ++i) {
		while (j > 0 && b[i] != a[j + 1]) j = nxt[j];
		if (b[i] == a[j + 1]) ++j;
		f[i] = f[i - j] + 1;
		if (j == 0) return printf("%d", -1), 0;
	}
	printf("%d", f[m]);
	return 0;
}