ABC232G

直接连边是 $\mathcal O(N^2)$ 的，考虑优化建图。构建 $M$ 个虚点，分别是 $\overline{0},\overline{1},\cdots,\overline{M-1}$。然后对于 $\forall k\in[0,M-1]$，连边 $\overline{k}\to \overline{(k+1)\bmod M}$，边权为 $1$。

对于 $\forall i\in[1,N]$，连边 $i\to \overline{-A_i+M}$，边权为 $0$。对于 $\forall i \in [1,N]$，连边 $\overline{B_i}\to i$，边权为 $0$。

借用一下官方题解的图：

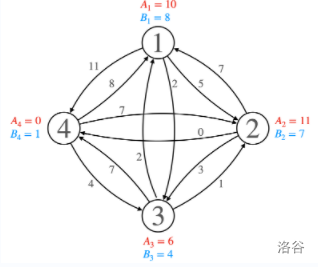
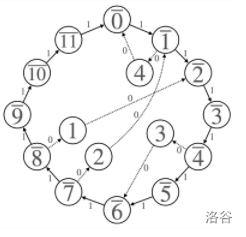
但是时间复杂度依旧寄。考虑继续优化，可以发现，环上有用的虚点个数至多 $2N$ 个，所以缩点，就可以了。

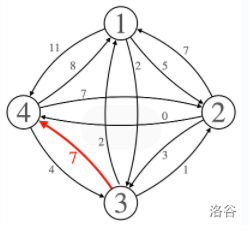
再借一下官方题解的图：

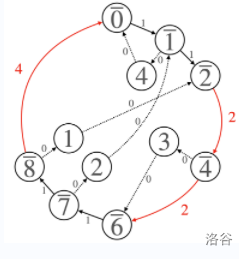
这样之后跑个 Dij 就好了。

Code：

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define fi first
#define se second
typedef pair <int, int> pii;
typedef long long ll;
const int N = 200005, M = 600005;
int n, m;
int a[N], b[N];
map <int, int> mp; int tot;
vector <pii> g[M];
ll dis[M]; bool vis[M];

void dij() {
	memset(dis, 0x3f, sizeof dis); dis[1] = 0;
	priority_queue <pii> q; q.push(pii(0, 1));
	while (!q.empty()) {
		int u = q.top().se; q.pop();
		if (vis[u]) continue;
		vis[u] = 1;
		for (auto e : g[u]) {
			int v = e.fi, w = e.se;
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				q.push(pii(-dis[v], v));
			}
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
	for (int i = 1; i <= n; ++i) scanf("%d", &b[i]);
	tot = n;
	for (int i = 1; i <= n; ++i) {
		if (!mp.count(b[i])) mp[b[i]] = ++tot;
		if (!mp.count(-a[i] + m)) mp[-a[i] + m] = ++tot;
		g[i].pb(pii(mp[-a[i] + m], 0));
		g[mp[b[i]]].pb(pii(i, 0));
	}
	for (auto cur : mp) {
		auto nxt = mp.upper_bound(cur.fi);
		if (nxt == mp.end()) nxt = mp.begin();
		auto tmp = *nxt;
		g[cur.se].pb(pii(tmp.se, (tmp.fi - cur.fi + m) % m));
	}
	dij();
	printf("%lld", dis[n]);
	return 0;
}