洛谷 P6453

设第 $i$ 列高 $h_i$，建立序列 $h_i$ 的小根笛卡尔树，然后树形 DP。

发现这样就将原来不规整的图形剖分成若干个矩形：

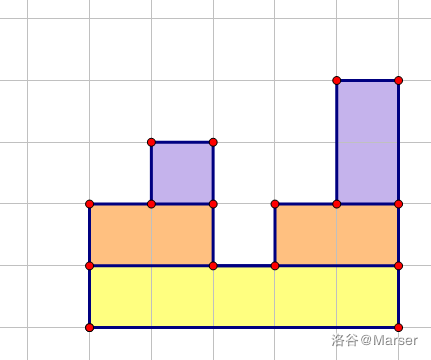
我们发现，这样构成的若干个矩形正好对应小根笛卡尔树上的所有节点，每次递归处理的两个小联通块正是当前节点的两个儿子。根据定义，对于节点 $x$ 代表的矩形，它的长度是 $siz_x$，高度为 $h_x-h_{fa_x}$。

设 $f_{i,j}$ 表示在 $i$ 的子树里放置 $j$ 个互不冲突的数的方案数，那么转移一是从子树里来，二是在自己所代表的矩形中填。

对于两棵子树合并，这很好处理，就是普通的树形背包，这部分是 $\mathcal O(n^2)$ 的。

对于第二种转移，我们枚举自己的矩形中放了几个车。如果我们要在 $n\times m$ 矩形中放 $k$ 个车，那么方案数是 $\binom n k\times \binom m k\times k!$，但要注意，我们还要枚举已经在儿子中放了几个车，因为儿子所占掉的列在这里是不能填的，因此这部分复杂度 $\mathcal O(n^2k)$。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 505, M = 1000005, mod = 1e9 + 7;
int n, k;
int a[N];
int fac[M], inv[M];
int stk[N], top, ch[N][2];
int f[N][N], tmp[N], siz[N];

int qpow(int x, int y) {
	int res = 1;
	while (y) {
		if (y & 1) res = 1ll * res * x % mod;
		x = 1ll * x * x % mod;
		y >>= 1;
	}
	return res;
}

void init(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; ++i) fac[i] = 1ll * fac[i - 1] * i % mod;
	inv[n] = qpow(fac[n], mod - 2);
	for (int i = n - 1; ~i; --i) inv[i] = 1ll * inv[i + 1] * (i + 1) % mod;
}

int C(int n, int m) {
	if (n < 0 || m < 0 || n < m) return 0;
	return 1ll * fac[n] * inv[n - m] % mod * inv[m] % mod;
}

void add(int &a, int b) {
	a += b;
	if (a >= mod) a -= mod;
}

void dfs(int u, int fa) {
	f[u][0] = siz[u] = 1;
	for (int i = 0; i < 2; ++i) {
		int v = ch[u][i];
		if (!v) continue;
		dfs(v, u);
		for (int j = 0; j <= siz[u] + siz[v]; ++j) tmp[j] = 0;
		for (int j = 0; j <= siz[u]; ++j)
			for (int k = 0; k <= siz[v]; ++k)
				add(tmp[j + k], 1ll * f[u][j] * f[v][k] % mod);
		for (int j = 0; j <= siz[u] + siz[v]; ++j) f[u][j] = tmp[j];
		siz[u] += siz[v];
	}
	for (int i = siz[u]; ~i; --i) {
		int sum = 0;
		for (int j = 0; j <= min(i, a[u] - a[fa]); ++j)
			add(sum, 1ll * C(siz[u] - (i - j), j) * C(a[u] - a[fa], j) % mod * fac[j] % mod * f[u][i - j] % mod);
		f[u][i] = sum;
	}
		
}

int main() {
	scanf("%d%d", &n, &k);
	init(M - 5);
	for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
	for (int i = 1; i <= n; ++i) {
		while (top && a[stk[top]] > a[i]) ch[i][0] = stk[top], --top;
		if (top) ch[stk[top]][1] = i;
		stk[++top] = i;
	}
	dfs(stk[1], 0);
	printf("%d", f[stk[1]][k]);
	return 0;
}