COCI 2021-2022 #5
COCI 2021-2022 #5 题解
T1:
简单模拟,贴个较为简洁的代码
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int T;
int n;
char s[N];
int cnt[26];
void solve() {
scanf("%s", s + 1), n = strlen(s + 1);
memset(cnt, 0, sizeof cnt);
int ty = 1, mul, sum;
for (int i = 1; i <= n; ++i) {
if (i == 1 || s[i - 1] == '+' || s[i - 1] == '>') {
mul = 1;
if (isdigit(s[i])) mul = s[i] - '0', ++i;
}
if (isalpha(s[i])) {
sum = 1;
if (isdigit(s[i + 1])) sum = s[i + 1] - '0';
cnt[s[i] - 'A'] += mul * sum * ty;
}
else if (s[i] == '-') ty = -1, ++i;
}
bool flag = 0;
for (int i = 0; i < 26; ++i) flag |= cnt[i];
if (flag) printf("NE\n");
else printf("DA\n");
}
int main() {
scanf("%d", &T);
while (T--) solve();
return 0;
}
T2:
简单模拟,不难发现直接模拟的复杂度为 \(\mathcal O(nm)\)。
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 2005;
int n, m, ans;
char mp[N][N];
bool chk(int x, int L, int R) {
for (int i = L; i <= R; ++i) if (mp[x][i] == '#') return true;
return false;
}
bool down(int x, int y, int len) {
for (int i = 1; i <= len; ++i)
if (x + len + i > n || y - len + i > m || y + len - i > m || mp[x + len + i][y - len + i] != '#' || mp[x + len + i][y + len - i] != '#' || chk(x + len + i, y - len + i + 1, y + len - i - 1))
return false;
return true;
}
bool up(int x, int y) {
for (int i = 1; i <= n; ++i) {
if (x + i > n || y - i < 1 || y + i > m || mp[x + i][y - i] != '#' || mp[x + i][y + i] != '#') return false;
if (chk(x + i, y - i + 1, y + i - 1)) return false;
if (down(x, y, i)) return true;
}
return false;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%s", mp[i] + 1);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (mp[i][j] == '#' && up(i, j))
++ans;
printf("%d", ans);
return 0;
}
T3:
咕咕咕,什么牛逼构造
Upd:私信了 AThousandSuns 大佬获得了解法(
考虑先求出循环:把镜子两边拆成两部分,对于 \(x\) 坐标相同,\(y\) 坐标相邻的两个半块镜子进行连边,\(y\) 坐标相同,\(x\) 坐标相邻同理。对于反射后到无穷远处的情况,建一个虚点与其连边。于是每个环就是一个循环。
然后把每个循环看成点,两个循环经过同一块镜子就连一条边,现在的问题就是给边四染色使得虚点之外的点连出的每种颜色的边数相同且为偶数,一个显然的必要条件是虚点之外点的度数都是 \(8\) 的倍数,构造说明这也是充分条件。
从虚点开始跑个欧拉回路,把所有边分成第奇数次经过和第偶数次经过的 \(2\) 个部分,分别对每个连通块跑欧拉回路,同样分成 \(2\) 部分,这 \(4\) 部分就是所求答案。时间复杂度 \(\mathcal O(n)\),常数蛮大的。
具体细节见代码。
Code:
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define fi first
#define se second
typedef pair <int, int> pii;
const int N = 2000005;
int n;
int ans[N];
int x[N], y[N], tmp[N], tl;
int head[N], ver[N], nxt[N], cnt;
int id[N], tot = 1;
bool vis[N], ty[N];
int deg[N];
vector <pii> vx[N], vy[N];
char s[2];
void add(int u, int v) {
ver[++cnt] = v, nxt[cnt] = head[u], head[u] = cnt;
}
bool dfs(int u, int fa) {
vis[u] = 1;
bool flag = false;
for (int i = head[u]; i; i = nxt[i]) {
int v = ver[i];
if (v == fa) continue;
if (vis[v]) flag = true;
else flag |= dfs(v, u);
}
if (flag) id[u] = tot + 1;
else id[u] = 1;
return flag;
}
void DFS(int u, int op) {
for (int &i = head[u]; i; i = nxt[i]) {
int v = ver[i], t = i;
if (vis[i >> 1]) continue;
vis[i >> 1] = 1;
if (op == -1)
DFS(v, op), ty[t >> 1] = tl ^= 1;
else if (ty[t >> 1] == op)
DFS(v, op), ans[t >> 1] = (tl ^= 1) + (op << 1) + 1;
}
}
void Clear() {
for (int i = 1; i <= 2 * n + 1; ++i) head[i] = vis[i] = 0;
cnt = 1;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d%s", &x[i], &y[i], s);
tmp[++tl] = x[i], tmp[++tl] = y[i];
ty[i] = s[0] == '/';
}
sort(tmp + 1, tmp + tl + 1);
tl = unique(tmp + 1, tmp + tl + 1) - (tmp + 1);
for (int i = 1; i <= n; ++i) {
x[i] = lower_bound(tmp + 1, tmp + tl + 1, x[i]) - tmp, y[i] = lower_bound(tmp + 1, tmp + tl + 1, y[i]) - tmp;
vx[x[i]].pb(pii(y[i], i)), vy[y[i]].pb(pii(x[i], i));
}
for (int i = 1; i <= tl; ++i) {
sort(vx[i].begin(), vx[i].end());
for (int j = 0; j < (int)vx[i].size() - 1; ++j) {
int a = vx[i][j].se, b = vx[i][j + 1].se;
a = 2 * a + 1 - ty[a], b = 2 * b + ty[b];
add(a, b), add(b, a);
}
sort(vy[i].begin(), vy[i].end());
for (int j = 0; j < (int)vy[i].size() - 1; ++j) {
int a = vy[i][j].se, b = vy[i][j + 1].se;
a = 2 * a + 1, b = 2 * b;
add(a, b), add(b, a);
}
}
for (int i = 2; i <= 2 * n + 1; ++i) if (!vis[i])
if (dfs(i, 0)) ++tot;
Clear();
for (int i = 1; i <= n; ++i) {
int x = id[2 * i], y = id[2 * i + 1];
add(x, y), add(y, x), ++deg[x], ++deg[y];
}
for (int i = 2; i <= tot; ++i) if (deg[i] % 8) return printf("%d", -1), 0;
tl = 0, DFS(1, -1);
for (int _ = 0; _ < 2; ++_) {
Clear();
for (int i = 1; i <= n; ++i) {
int x = id[2 * i], y = id[2 * i + 1];
add(x, y), add(y, x);
}
for (int i = 1; i <= tot; ++i) DFS(i, _);
}
for (int i = 1; i <= n; ++i) printf("%d ", ans[i]);
return 0;
}
T4:
直接判断不好搞,考虑两个数不互质的情况,这时这两个数至少有一个质因子相同。
所以在这题中一个数和它的质因子集合是等价的,
这启示我们建一个新序列,新序列里的每一个数都是原序列中某个数的质因子,原序列中的一个数在新序列中对应一段区间,在原序列中询问一段区间也变为了新数列中询问一段区间。
由于每一个数的质因子不是很多,建出来的新序列也不会很长(大概算一下长度没有超过 \(3\times 10^6\))。
于是我们就相当于要在新序列上求一段区间内有没有两个相同的数,如果有相同,就说明有不互质的数。
这个问题如果是不修改很容易做,只用记录对于每个数,上一个和它相同的数的位置,然后做一遍前缀 \(\max\) 得到一个新数组,设为 \(P\)。
每次查询 \(l,r\) 就相当于查询 \(P_r\) 是否大于等于 \(l\)。
上面所说的大概就是这一题的做法,不懂的可以先做这题。
现在考虑如果动态修改该怎么做,由于要动态修改,预处理行不通了,得寻找新方法。对于每个值,为了快速找到上一个与它相同的数,我们要记录值为该值的数的位置,由于要修改,还得支持快速插入删除定位,而这可以用 set 来完成。
之前的方法要维护前缀最大值,现在加上了单点修改,可以用线段树轻松维护。
常数非常大,有点卡,可能需要离散化一下,只将在修改中出现的位置分解质因数构成新序列。这样就可以显著减小常数。
Code:
#include <bits/stdc++.h>
using namespace std;
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)
const int N = 1000000, M = 2000000;
int n;
int Low[M];
int L[M], R[M], st[N], ed[N];
bool vis[M], now[M];
int M1[M], M2[M], k;
set <int> pos[M];
char ch[N][3];
int P[12], tot;
int A[M*3], tot1;
int mx[M*10];
void change(int p, int l, int r, int x, int v) {
if (l == r) return mx[p] = v, void();
int mid = l + r >> 1;
if (x <= mid) change(ls(p), l, mid, x, v);
else change(rs(p), mid + 1, r, x, v);
mx[p] = max(mx[ls(p)], mx[rs(p)]);
}
int query(int p, int l, int r, int x, int y) {
if (x <= l && r <= y) return mx[p];
int mid = l + r >> 1, res = 0;
if (x <= mid) res = max(res, query(ls(p), l, mid, x, y));
if (y > mid) res = max(res, query(rs(p), mid + 1, r, x, y));
return res;
}
bool Ask(int x, int y) {
if (st[x] > ed[y] || x > y) return false;
if (query(1, 1, tot1, st[x], ed[y]) >= st[x]) return true;
return false;
}
void del(int x) {
now[x] = 0;
for (int i = st[x]; i <= ed[x]; ++i) {
pos[A[i]].erase(i);
auto it = pos[A[i]].lower_bound(i);
if (it != pos[A[i]].end()) {
if (it != pos[A[i]].begin()) {
int X = (*it); --it;
int Y = (*it);
change(1, 1, tot1, X, Y);
}
else {
int X = (*it);
change(1, 1, tot1, X, 0);
}
}
change(1, 1, tot1, i, 0);
}
}
void ins(int x) {
now[x] = 1;
for (int i = st[x]; i <= ed[x]; ++i) {
auto it = pos[A[i]].lower_bound(i);
if (it != pos[A[i]].end())
change(1, 1, tot1, *it, i);
if (it != pos[A[i]].begin())
--it, change(1, 1, tot1, i, *it);
pos[A[i]].insert(i);
}
}
int main() {
int _; scanf("%d%d", &_, &n);
memset(Low, 0x3f, sizeof Low);
for (int i = 2; i <= N; ++i)
if (!vis[i])
for (int j = i; j <= N; j += i)
vis[j] = 1, Low[j] = min(Low[j], i);
memset(vis, 0, sizeof vis);
for (int i = 1; i <= n; ++i) {
scanf("%s%d", ch[i], &L[i]);
if (ch[i][0] == 'C') scanf("%d", &R[i]);
else vis[L[i]] = 1;
}
for (int i = 1; i <= N; ++i) if (vis[i]) {
M1[i] = ++k, M2[k] = i;
tot = 0, P[0] = -1; int x = i;
while (x > 1) {
if (P[tot] != Low[x]) P[++tot] = Low[x];
x /= Low[x];
}
st[k] = tot1 + 1;
for (int i = 1; i <= tot; ++i) A[++tot1] = P[i];
ed[k] = tot1;
}
for (int i = 1; i <= n; ++i) {
if (ch[i][0] == 'S') {
int p = M1[L[i]];
if (now[p]) del(p);
else ins(p);
}
else {
int x = lower_bound(M2 + 1, M2 + k + 1, L[i]) - M2, y = upper_bound(M2 + 1, M2 + k + 1, R[i]) - M2 - 1;
printf("%s\n", Ask(x, y) ? "DA" : "NE");
}
}
return 0;
}
T5:
注意到题目要求实际就是让强连通分量的个数尽可能小,并给出构造方案。
先考虑把边的方向确定下来。
发现有贡献的连法只有 \(3\) 种,上面是上河岸,下面是下河岸。
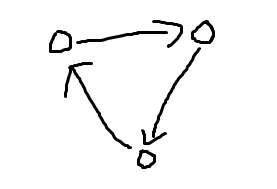
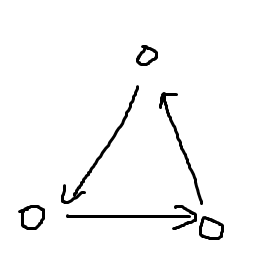
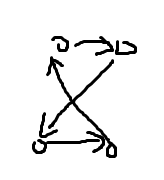
观察发现,这三种连法中右下的点一定是向左上连出的。
根据这个发现,我们有了以下思路:
将边排序,按第一关键字 \(x\) 从小到大(上河岸),第二关键字 \(y\) 从大到小(下河岸)。
枚举每条边,如果当前边下河岸的点在目前所有边的最右端,那么说明这个点在某种连法中一定处在右下的位置,所以此边的类型为 \(1\)。
其余边类型为 \(0\)。
现在已经确定了边的方向,剩下的就跑一遍 Tarjan 好了。
具体细节看代码
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 400005;
int a, b, m;
int head[N], ver[N*2], nxt[N*2], cnt;
struct node {
int x, y, id;
} p[N];
int dfn[N], low[N], tim;
bool vis[N]; int stk[N], top;
int ans;
bool ty[N];
void Tarjan(int u) {
dfn[u] = low[u] = ++tim, vis[stk[++top] = u] = 1;
for (int i = head[u]; i; i = nxt[i]) {
int v = ver[i];
if (!dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
else if (vis[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++ans;
do {
vis[stk[top]] = 0;
--top;
} while (stk[top + 1] ^ u);
}
}
void add(int u, int v) {
ver[++cnt] = v, nxt[cnt] = head[u], head[u] = cnt;
}
int main() {
scanf("%d%d%d", &a, &b, &m);
for (int i = 1; i < a; ++i) add(i, i + 1);
for (int i = 1; i < b; ++i) add(i + a, i + a + 1);
for (int i = 1; i <= m; ++i) scanf("%d%d", &p[i].x, &p[i].y), p[i].id = i;
sort(p + 1, p + m + 1, [](node x, node y) {
return x.x != y.x ? x.x < y.x : x.y > y.y;
});
for (int i = 1, mx = 0; i <= m; ++i) {
if (p[i].y > mx) mx = p[i].y, ty[p[i].id] = 1, add(p[i].y + a, p[i].x);
else ty[p[i].id] = 0, add(p[i].x, p[i].y + a);
}
for (int i = 1; i <= a + b; ++i) if (!dfn[i]) Tarjan(i);
printf("%d\n", ans);
for (int i = 1; i <= m; ++i) printf("%d ", ty[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号