洛谷 P7931

以下标为横坐标，值为纵坐标，建立坐标系。
然后会发现每个点的后继在其右上方。
按照每个点 LIS 大小来分层，以样例 $3$ 为例：

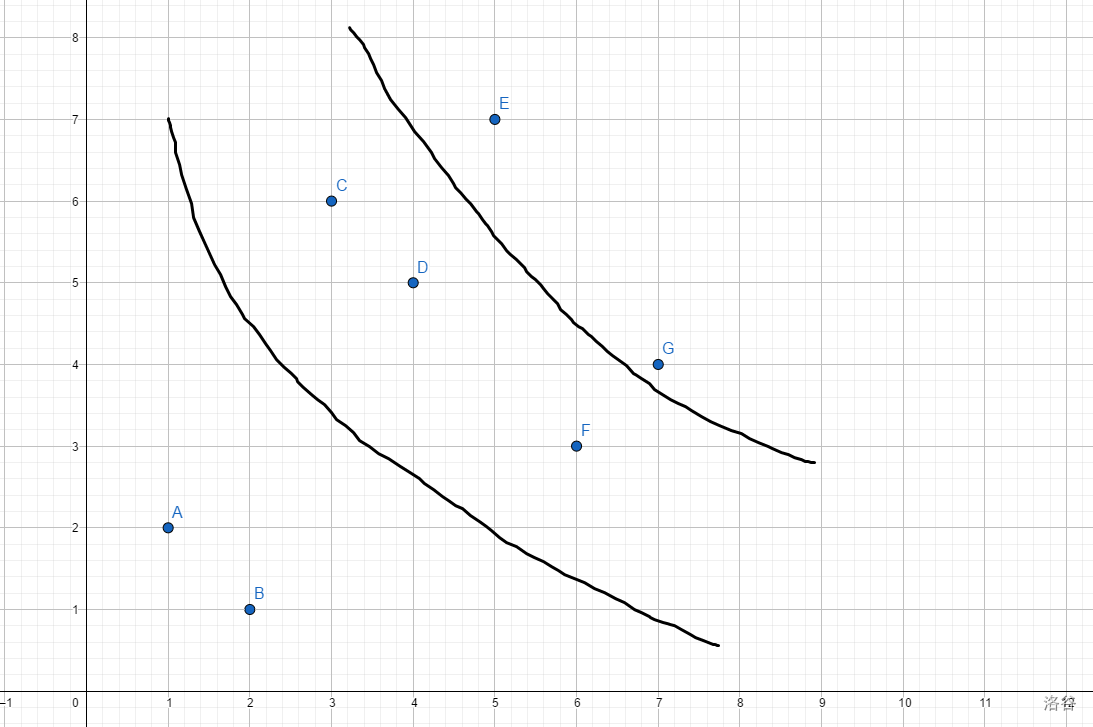
注意到同层之间一定满足 $x$ 递增 $y$ 递减。

结论：存在一种选择 LIS 的最优方案，满足每个 LIS 在图上不交叉。
如样例 $3$ 选的两组 LIS 就是 $A,C,E$ 与 $B,F,G$，显然没有交叉。
证明：以这种情况为例，

如果 $A$ 选了 $D$，但是 $B$ 不能选 $C$。
如果 $A$ 选了 $C$，$B$ 也能选 $D$。

Code：

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define pp pop_back
const int N = 1000005;
int n;
int a[N];
int dp[N], len;
vector <int> vec[N], tmp;
vector <vector <int> > ans;

void solve() {
	while (1) {
		if (tmp.empty())
			if (vec[1].empty()) break;
			else tmp.pb(vec[1].back()), vec[1].pp();
		else if (tmp.size() == len) ans.pb(tmp), tmp.clear();
		else {
			int k = tmp.size() + 1, cur = tmp.back();
			while (vec[k].size() && vec[k].back() < cur) vec[k].pp();
			if (vec[k].empty() || a[cur] > a[vec[k].back()]) tmp.pp();
			else tmp.pb(vec[k].back()), vec[k].pp();
		}
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
	for (int i = 1; i <= n; ++i) {
		if (dp[len] < a[i]) { dp[++len] = a[i], vec[len].pb(i); }
		else {
			int p = lower_bound(dp + 1, dp + len + 1, a[i]) - dp;
			dp[p] = a[i], vec[p].pb(i);
		}
	}
	for (int i = 1; i <= n; ++i) reverse(vec[i].begin(), vec[i].end());
	solve();
	printf("%d %d\n", ans.size(), len);
	for (auto i : ans) {
		for (auto x : i) printf("%d ", x);
		printf("\n");
	}
	return 0;
}