CF1089I

考虑用总数（$n!$）减去不合法的排列数。我们现在要研究不合法的排列长什么样。
称【将子段排序后是连续的一段数值】的子段称为不合法子段。那么合法的排列，就是不存在长度在 $[2,n−1]$ 中的不合法子段的排列。
称一个不合法子段是极长的，当且仅当不存在另一个长度小于 $n$ 的不合法子段包含它。发现，两个不合法子段如果有交，则它们的并也是不合法子段。因此，不合法的排列只有如下两种可能：

• 由两段极长不合法子段组成，这两段不合法子段可能相交。形式化地，若这两个子段分别是 $[l_1,r_1],[l_2,r_2]$，则 $l_1=1,r_2=n$，且 $r_1\ge l_2−1$。
• 由三段及以上的极长不合法子段拼成，它们互不相交。形式化地，若这些子段分别是 $[l_1,r_1],[l_2,r_2],\cdots,[l_k,r_k]$，则 $l_1=1,r_k=n$，且 $\forall i,1\le i\lt k,r_i+1=l_{i+1}$。
  

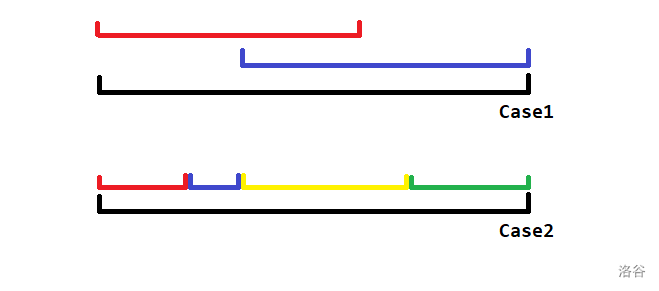
上述两种情况，不重不漏地刻画了所有不合法排列。因此只需要对这两种情况分别计数。
设长度为 $i$ 的合法排列数为 $f_i$，也就是答案。
第一种不合法排列：发现两个子段中，必有一个包含的数值为 $1,2,\cdots,i$（其中 $i$ 是子段长度）。不妨假设它是左边的子段，然后把方案数乘以 $2$ 即可。设 $h_i$ 表示有多少长度为 $i$ 的排列，满足它的任何长度 $\lt i$ 的前缀，不是【数值的一个前缀】。形式化地 $\forall j,1\le j\lt i,\left\{p_k|k\le j\right\}\ne\left\{1\cdots j\right\}$。求 $h_i$，可以继续使用【总数减不合法数量】的思想：$h_i=i!-\sum_{j=1}^{i-1}h_j\times(i−j)!$。求出 $h_i$ 后，第一种不合法的排列数量是 $2\times \sum_{i=1}^{n-1}h_i\times(n−i)!$。也就是枚举了左边子段的长度，后面的数可以任意排列：因为不管左边怎么样，后面任意排列，至少自己内部是一个不合法子段（$i+1\cdots n$，连续的数值）；当然，它可能还能向左延伸一点，也就是两个子段有交。
第二种不合法排列：考虑设 $g_{i,j}$ 表示 $i$ 个数，划分为 $j$ 个不合法子段的方案数（不一定极长）。则 $g_{i,j}=\sum_{k=1}^{i}g_{i-k,j-1}\times k!$，其中 $k$ 是枚举最后一个不合法子段的长度（这个子段内部可以任意排列，也就是 $k!$ 种方案）。初始值是 $g_{0,0}=1$。注意，这里没有考虑子段的相对顺序，也就是最后一个子段里的数值，默认为 $i−k+1\cdots i$。给此时的 $j$ 个子段依次编号为 $1\cdots j$。现在要求 $j$ 个子段都是极长的，那么相当于 $1\cdots j$ 这些子段的子段，不能有连续数值，也就是：$\sum_{j=3}^{n-1}g_{n,j}\times f_j$。
综上所述：$f_n=n!-2\times \sum_{i=1}^{n-1}h_i\times(n−i)!-\sum_{j=3}^{n-1}g_{n,j}\times f_j$。
预处理答案，时间复杂度为 $\mathcal O(n^3)$。

Code：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 405;
int T;
int n, mod;
int fac[N];
int f[N], h[N], g[N][N];

void add(int &a, int b) { a += b; if (a >= mod) a -= mod; }
void sub(int &a, int b) { a -= b; if (a < 0) a += mod; }

void init(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; ++i) fac[i] = 1ll * fac[i - 1] * i % mod;
	h[1] = 1;
	for (int i = 2; i <= n; ++i) {
		h[i] = fac[i];
		for (int j = 1; j < i; ++j)
			sub(h[i], 1ll * h[j] * fac[i - j] % mod);
	}
	g[0][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= i; ++j)
			for (int k = 1; k <= i; ++k)
				add(g[i][j], 1ll * g[i - k][j - 1] * fac[k] % mod);
	f[1] = 1, f[2] = 2;
	for (int i = 3; i <= n; ++i) {
		for (int j = 1; j < i; ++j)
			add(f[i], 1ll * h[j] * fac[i - j] % mod);
		add(f[i], f[i]);
		for (int j = 3; j < i; ++j)
			add(f[i], 1ll * g[i][j] * f[j] % mod);
		f[i] = (fac[i] - f[i] + mod) % mod;
	}
}

void solve() {
	scanf("%d", &n);
	printf("%d\n", f[n]);
}

int main() {
	scanf("%d%d", &T, &mod);
	init(400);
	while (T--) solve();
	return 0;
}