数论专题

数论好难啊QAQ

----------------------------------------------------------------------------------

先来一些基本的数论必备代码

（1）欧拉筛

const int MAXN=3000001;
int prime[MAXN];//保存已经求出的素数
bool vis[MAXN];//判断是不是素数
int Prime(int n)
{
    int cnt=0;
    memset(vis,0,sizeof(vis)); //vis[]=0指是素数
    for(int i=2;i<n;i++)
    {
        if(!vis[i])
        prime[cnt++]=i;
        for(int j=0;j<cnt&&i*prime[j]<n;j++)
        {
            vis[i*prime[j]]=1;
            if(i%prime[j]==0)//欧拉筛法的精髓之处，目的是为了不重复筛除数据
            break;
        }
    }
    return cnt;//返回小于n的素数的个数
}

具体的之前博客有写：https://www.cnblogs.com/Knightero/p/12778655.html

（2）gcd与lcm

int gcd( int  a,int b)
{ return b==0?a:gcd(b,a%b); }

int lcm(int a,int b)
{
return a/gcd(a,b)*b;
}

(3)快速幂

int quick_pow(int x,int n,int mod){
    int res = 1;
    while(n > 0){
        if(n & 1)    res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
} 

------------------------------------------------------------------------------------------

新学习到的知识

（1）求逆元

运用费马小定理求逆元（其实不难）

(a/b)%mod不等于(a%mod/b%mod)%mod;

但是a/b可以看成a*b^-1

把除法转换为乘法来运算

逆元就是研究怎么已知b算出b^-1（且要有%mod，不然直接除就好了）

这时候出现了费马小定理

 

 所以要计算（a/b）%mod=(a*b^-1)%mod=(a*b^(p-2))%mod

而此刻我们会求b^(p-2)，利用快速幂可求

long long int quick_pow(long long int a, long long int b)
{

    long long int ans = 1;
    while (b) {
        if (b & 1) ans = (ans * a) % mod;
        b >>= 1;
        a = (a * a) % mod;
    }
    return ans;
}
long long int inv(long long int a, long long int b)//求（a/b）%mod
{
    return a * quick_pow(b, mod - 2) % mod;
}

 （2）欧拉函数

学习视频：https://www.bilibili.com/video/BV1p741117w4?from=search&seid=17822651721941687634

欧拉函数就是给定一个n，求小于等于n中与n互质的数有几个

int Euler(int n)
{
    int res = n;
    for (int i = 2; i <= n; i++)
    {
        if (n == 1)break;
        if (n % i == 0)
        {
            res = res / i * (i - 1);//这步在视频9：15处
        }
        while (n % i == 0) n /= i;
    }
    return res;
}

 （3）欧拉函数打表

利用公式

 

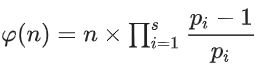
 先给全体phi【】附上i的值，起到了公式中n的作用，然后 i == phi[i]，说明是质数（为什么是质数往后看）

确定是质数之后，遍历质数的倍数，因为质数的倍数根据唯一分解定理肯定会含有此质数

然后对这个倍数利用公式修改其phi值

void EulerMeter() {
    for (int i = 1; i < N; i++)
        phi[i] = i;
    for (int i = 2; i < N; i++)
    {
        if (i == phi[i])
        {
            for (int j = i; j < N; j += i)
            phi[j] = phi[j] / i * (i - 1);
        }
    }
}