线性基

概念

线性基是向量空间的一组基，通常可以解决有关异或的一些题目。 ——OI Wiki

说实话我感觉上面这句只能解释为啥这玩意的名字是线性基这仨字。

其实线性基就是一个集合，本质是通过对二进制的判断来从原集合中取出一些数成为个新的集合。

具体怎么样下面会讲到。

\[\]

性质

1. 线性基具有普通集合所具有的性质，即确定性、互异性、无序性。

2. 线性基中每个数二进制下的 \(1\) 的最高位都是不同的。

3. 线性基中没有异或和为 \(0\) 的子集。

4. 线性基中任意多元素的异或和的值域等于原集合中任意多元素的异或和的值域。

5. 线性基在满足上一个条件的情况下，所包含元素个数是最少的。

6. 线性基中不同的元素异或出来的值是不同的。

\[\]

构造

线性基最常处理的问题就是，求一个集合中任意元素异或和的最大值。

对于这种问题，用脚趾头想想它也不能让你暴力过，所以我们考虑贪心。

首先，异或的原则是，如果异或的两个数的二进制某一位不同则这一位为 \(1\)，否则为 \(0\)。

并且，异或满足交换律，即同一个集合中的元素全部异或起来时，其答案与异或的顺序无关。

所以我们考虑什么时候它的异或和最大。显然是使最终值的二进制下的 \(1\) 越多越好。

但是单靠这一条信息似乎无从下手，所以我们从另一个方向思考。

一个数越大，它的二进制位数越多。换句话说，一个数越大，那么最高位的 \(1\) 越靠前。

因为异或都是按位异或，所以当前面位的值确定以后，后面位的值再怎么异或都不会对前面造成影响了。

所以具体构造方法如下：

假设我们要插入一个数 \(x\)，\(x\) 的最高位为 \(d\)。

• 若 \(d\) 位还未插入值，则插入 \(x\)；
• 若 \(d\) 位已经有值 \(y\)，则 \(x\gets x\oplus y\)，并继续向低位扫描，直到被插入或者变成 \(0\)。

可能有人不理解，为什么最高位有值时要异或上那个值。

因为任何一个数二进制的最高位都是 \(1\)。在同一个位置遇到了已经插入过的数证明两个数最高位相同，此时异或一下，使要插入的值最高位变成 \(0\)，再去判断新的最高位找一个新的位置插入。是为了尽可能使二进制的每一位都可以有 \(1\)，且可以证明对答案无影响。

最后将原集合中的所有元素都按上述方法尝试插入后，再从得到的线性基中不断异或取最大值即可。

void insert(int k){
  for(int i=len;i>=0;i--){
    if(!(k&(1ll<<i))) continue;//如果当前这一位不是 1 插入也没用
    if(!p[i]){p[i]=k;return;}//插入
    k^=p[i];//否则不断异或变小
  }
}

当然线性基还有很多别的操作，可以类比很多别的知识点。但是我觉得我用不到而且我很懒，所以就先不提了。

\[\]

例题

[BJWC2011]元素

给出 \(n\) 种元素，每种元素 \(i\) 有 \(a_i\) 和 \(b_i\) 两种性质。
要求从中选出一些元素成为一个新的集合，满足这个集合中的任意元素的 \(a\) 的异或和不为 \(0\)，并使 \(b\) 的加和尽可能大。
\(1\le n\le 1000,1\le a_i \le 10^{18},1\le b_i\le 10^4\)

首先考虑第一个条件，任意元素的异或和不为 \(0\)。

只要保证异或的元素的 \(a\) 的二进制中有任意一位不同即可。

换做到线性基中，只要 \(a\) 二进制有一位和其他的都不一样的就会被插入。所以我们判断能否被插入即可。

接下来考虑第二个条件，使 \(b\) 的加和尽可能大。

想一下，如果一个元素越早被扫描，那么它被插入的可能就越大。

所以我们贪心地对所有元素按 \(b\) 为关键值排序，优先尝试插入 \(b\) 较大的数，可以保证最后集合中所有元素的 \(b\) 的加和最大。

bool insert(int k){
  for(int i=len;i>=0;i--){
    if(!((1ll<<i)&k)) continue;
    if(!p[i]){p[i]=k;return true;}
    k^=p[i];
  }
  return false;
}

bool cmp(node x,node y){
  return x.mag>y.mag;
}

signed main(){
  n=read();
  for(int i=1;i<=n;i++)
    a[i].num=read(),a[i].mag=read();
  sort(a+1,a+n+1,cmp);
  for(int i=1;i<=n;i++){
    if(insert(a[i].num))Ans+=a[i].mag;
  }
  printf("%lld\n",Ans);
  return 0;
}

[TJOI2008]彩灯

有 \(n\) 盏灯与 \(m\) 个开关，每个开关可以控制特定的几个灯。
现在给出每个开关与灯的对应关系，求这些灯最多可以展现多少种样式。
ps：从数学的角度看，这一排彩灯的任何一个彩灯只有亮与不亮两个状态，所以共有 \(2^n\) 种样式。
\(1\le n,m\le 50\)。

看到 \(n\) 如此之小，结合他给出的输入形式，不难想到将每个开关所控制的灯的形式转化为二进制。

把每个灯泡看做一个二进制位，每个开关看成一个由所控制的灯泡形成的二进制转化来的十进制数。

看上去有点抽象？那来解释一下为什么这么转化。

每个灯泡都有关或不关两种状态，且同一个开关所控制的若干个灯泡只能同时开或关。

同一个彩灯，若开关 \(a\) 使它打开，开关 \(b\) 再使它关闭，就相当于两个数在这一位的异或结果。

我们就把每个开关所控制的彩灯转化成二进制，然后在线性基插入对应十进制数。

对于线性基的每个数我们可以选或者不选，也就相当于这个开关开或者不开。

由于线性基中任意多的元素异或和的值域等于原集合中任意多元素异或和的值域，且任意多元素的异或和都不同，所以可以保证情况不重不漏。

最后假设我们插入了 \(k\) 个元素，每个元素可以选或不选，所以有 \(2^k\) 种情况。

void insert(int k){
  for(int i=len;i>=0;i--){
    if(!(k>>i&1)) continue;
    if(!p[i]){cnt++,p[i]=k;return;}
    k^=p[i];
  }
}

signed main(){
  n=read();m=read();
  for(int i=1,lenth,val=0;i<=m;i++,val=0){
    cin>>s;lenth=strlen(s);
    for(int j=0;j<lenth;j++)
      val+=(1ll<<(n-j))*(s[j]=='O');
    insert(val);
  }
  printf("%lld\n",(1ll<<cnt)%Mod);
  return 0;
}

[WC2011]最大XOR和路径

给定一张无向图，n 个点，m 条边。
求一条从 \(1\) 到 \(n\) 的路径，使得路径上权值的异或和最大。
路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算异或和时也要被计算相应多的次数。
\(1\le n\le 50000,1\le m\le 100000,1\le d_i \le 10^{18}\)，其中 \(d_i\) 是第 \(i\) 条边的边权。

这题不太好想。

由于可以重复经过某些点或边，所以对于下面这张图：

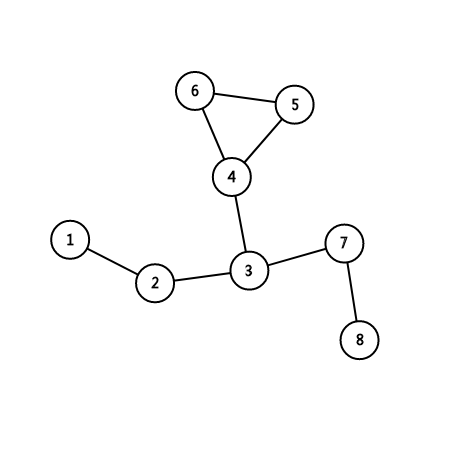
我们要从 \(1\) 走到 \(8\)，可以走 \(1\to 2\to 3\to 7\to 8\) 这条路线。

也可以走 \(1\to 2\to 3\to 4\to 6\to 5\to 4\to 3\to 7\to 8\) 这条路线。

可以发现，第二种路线比第一种路线多走了一个环，所以路径异或值会多异或这个环上的边权。而 \((3,4)\) 这条边由于走了两边，异或和为 \(0\)，所以对结果有贡献的只有环上权值的异或和，链接环与第一条路线中间的边根本不需要算贡献。

因此我们可以先找出一条从 \(1\) 到 \(n\) 的无环路径，算出路径上初始的异或和，再算出每个环的异或和，异或各个环求最大值即可。

多个元素异或求最值，那不是线性基干的事吗？

所以思路就很明确了，把每个环的异或值插入到线性基中，然后再以初始路径的异或和从中选择来找最大异或和。

至于初始路径怎么选，其实随便选择一条就可以了。

比如下面这个图：

显然，选择 \(1\to 4\to 5\to 6\) 比选择 \(1\to 2\to 3\to 6\) 要更优。

但是如果我们一开始随机选择了后者该怎么办。

我们发现整张图是一个大环，我们用我们选择的路径去异或这个大环的路径，我们选择的路径的贡献就会被抵消，因此可以得到前者这个更优的路径。

所以一开始随便选择无环路径即可。

void insert(int k){
  for(int i=len;i>=0;i--){
    if(!(k&(1ll<<i))) continue;
    if(!p[i]){p[i]=k;return;}
    k^=p[i];
  }
}

void dfs(int x,int res){
  Dis[x]=res;vis[x]=true;
  for(int i=head[x];i;i=e[i].nxt){
    int to=e[i].to;
    if(!vis[to]) dfs(to,Dis[x]^e[i].dis);
    else insert(Dis[x]^Dis[to]^e[i].dis);
  }
}

int query(int res){
  int ans=res;
  for(int i=len;i>=0;i--)
    if(p[i]) ans=max(ans,ans^p[i]);
  return ans;
}

signed main(){
  n=read();m=read();
  for(int i=1,fr,to,dis;i<=m;i++){
    fr=read();to=read();dis=read();
    add(fr,to,dis);add(to,fr,dis);
  }
  dfs(1,0);
  printf("%lld\n",query(Dis[n]));
  return 0;
}