哈夫曼树 Huffman
一些定义
PL
树的路径长度,即树根到每个叶节点的距离之和。
WPL
树的带权路径长度,即树根到每个叶节点的距离与每个叶结点权值的乘积之和。
哈夫曼树,也叫 Huffman 树,就是 WPL 最短的一种最优多叉树。
哈夫曼树的构造
对于哈夫曼树的构造,我们以二叉哈夫曼树为例:
我们每次选择两棵根节点权值最小的树,将它们的根节点合并成一棵新树。
原来的两个根节点成为为新树的根节点的儿子。新树的根节点权值为合并的两个根节点权值之和。
假设我们要构造一棵初始有五个节点的二叉哈夫曼树,权值分别为 \(1,2,4,6,8\),则它们的构建过程如下:
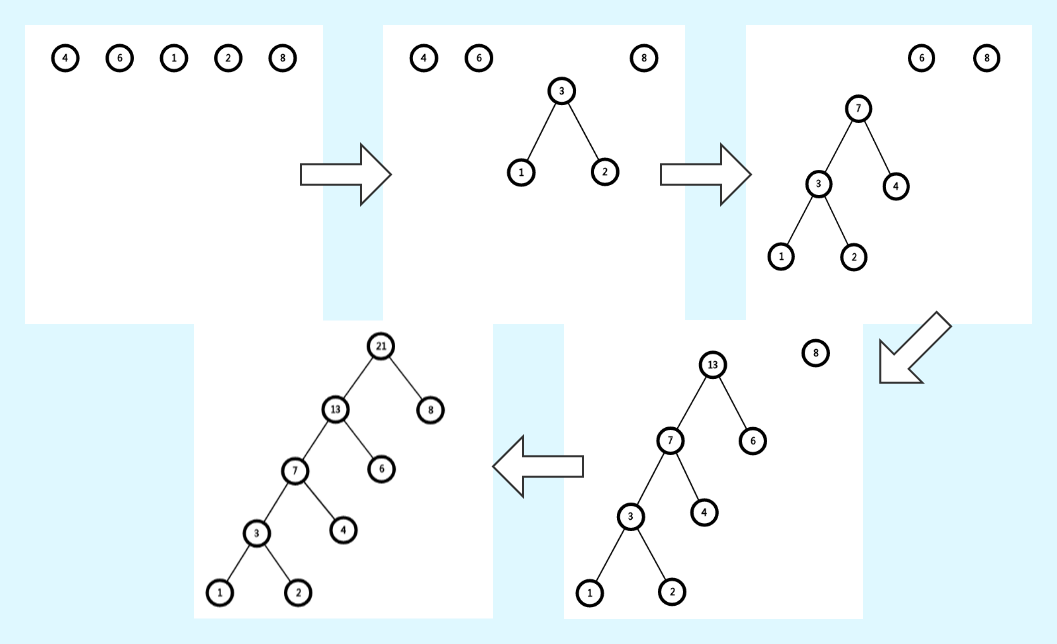
(我腾讯文档没有 VIP 所以下载不了高清图片,只能将就看吧 qwq)
注意,哈夫曼树中允许多个点有相同的权值。
关于 K 叉哈夫曼树的构造
假设我们要构造一棵 \(k\) 叉哈夫曼树 \((k>2)\)。
根据以上对哈夫曼树构造的原理,可以发现,这个构造方法是基于贪心的思想。每次取出最小的 \(k\) 个节点来合并成新的节点。
但是如果最后一步合并时,可选节点的数量不足 \(k\) 个,就会出现合并后的哈夫曼树根节点的儿子数小于 \(k\) 的情况。
此时它就不是一颗 WPL 最小的最优 \(k\) 叉树。因为此时我们随便取一个叶节点当做根节点的儿子,都可使 \(\sum (w_i\times l_i)\) 的值变小。
所以我们要满足 \((k-1)\mid (n-1)\) 这个条件时,才能使构造的 \(k\) 叉哈夫曼树达到最优。
而要满足这个条件,我们可以不断向图中加入权值为 \(0\) 的节点。显然 \(0\) 节点一定会先合并,这样可以使有权节点的深度降低。
哈夫曼编码
哈夫曼编码的原则是:编码从叶子节点到根节点,译码从根节点到叶子节点。
但其实这句话对下面的内容并没有什么帮助。
我们还是以二叉哈夫曼树为例。
对于一棵二叉哈夫曼树,我们从根节点开始,对左子树编码 \(0\),对右子树编码 \(1\),直到遍历完整棵树。
此时我们再从根节点出发,将路径上的编码排列起来,一直到某个根节点,此时的编码串就是该根节点的哈夫曼编码。
举个例子,我们有一串电文 AMCADEDDMCCAD,需要将其翻译成 01 串,并使其尽量短。
我们统计每个字符的出现次数,可得到如下数据:
\(\begin{array}{ccc} E & M & C & A & D \\ \hline 1 & 2 & 3 & 3 & 4\\ \end{array}\)
我们将每种字符的出现次数作为节点的权值,可建造一棵如图所示的二叉哈夫曼树:
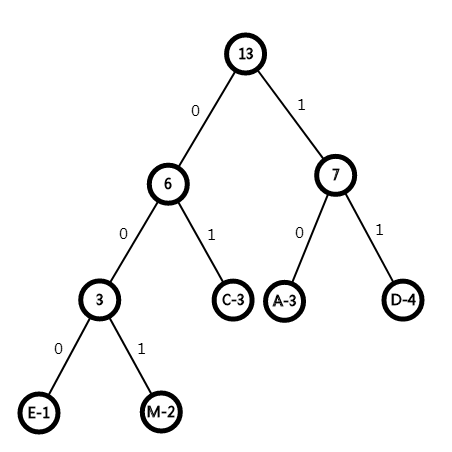
所以可得到各个字符的哈夫曼编码:
\(\begin{array}{c|cc} E&001\\ M&000\\ C&01\\ A&10\\ D&11\\ \end{array}\)
根据哈夫曼编码的定义,我们也可以看出,每种字符的编码长度之和为 PL,而每种字符的编码长度与其出现次数的乘积之和为 WPL。
此时的 PL 不一定是最短的,但 WPL 一定是最短的,只有这样才能使原串翻译后的 01 串最短。
当然上面只是说二叉哈夫曼树,其编码也只包含两种字符。假若要用 \(k\) 进制数来表示一个字符串,我们可以将其建成 \(k\) 叉哈夫曼树 \((k\ge 2)\)。
对于代码的具体实现,结合下面的例题来说。
例题
[NOI2015] 荷马史诗
有一个由 \(n\) 种字符组成的字串,给出这 \(n\) 种字符的出现次数,用 \(k\) 进制数来表示这个字符串。
求出这个 \(k\) 进制数的最短长度,并求出此时编码最长的字符的最短编码长度。
NOI 出模板题(
直接根据每种字符的出现次数建 \(k\) 叉哈夫曼树。
第一问就是 WPL 的长度,第二问就是在树中深度最大的字符的深度减一。
至于实现,我们运用优先队列存储每个节点的权值和深度,并按权值为第一关键字,深度为第二关键字从大到小排序。
首先将每个节点自己作为一棵树,放到优先队列中,并不断加入 \(0\) 节点直到满足条件为止。
每次取出 \(k\) 个节点来合并,同时统计 WPL。最后优先队列中只剩一个节点,输出统计结果与其深度减一即可。
struct node{
int w,h;
bool operator < (const node &a) const{
return a.w==w?h>a.h:w>a.w;
}
};
signed main(){
n=read();k=read();priority_queue<node> q;
for(int i=1,w;i<=n;i++) w=read(),q.push((node){w,1});
while((q.size()-1)%(k-1)) q.push((node){0,1});
while(q.size()>=k){
int h=-1,w=0;
for(int i=1;i<=k;i++){
node t=q.top();q.pop();
h=max(h,t.h);w+=t.w;
}
ans+=w;
q.push((node){w,h+1});
}
printf("%lld\n%lld\n",ans,q.top().h-1);
return 0;
}
写在后面
没啦,啥都没啦。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号