失配树

注：本文中字符串下标均从 $1$ 开始。

先看一个简单的问题：

给出一个字符串 $S$，求 $S$ 两个长度分别为 $n$ 和 $m$ 的前缀的最长公共 border 长度。

A：我暴力找！

$1\le n,m\le |S|\le 10^6$。

A：我加个哈希！

$T$ 组询问，$T\le 10^5$。

A：……

此时就需要我们的失配树了。

我们先来看一组样例：

假设这是我们找出的一个字符串的两个前缀。我们可以发现它们的最长公共 border 长度是 $3$。

说到求 border，怎么少的了我 KMP 呢？既然两个字符串都是同一个串的前缀，那么其中一个（较短的）必定也是另一个（较长的）字符串的前缀。

然后我们将其中较长的一个字符串的字符下标及其 $\text{nxt}$ 数组列出来看看。

$\begin{array}{c|lcr} 下标 & \text{nxt} \\ \hline 1 & 0\\ 2 & 0\\ 3 & 1\\ 4 & 2\\ 5 & 3\\ 6 & 4\\ \end{array}$

能看出什么东西吗？不能？那我们建成一棵树看看？

接下来，我们连边 $(\text{nxt}[i],i),i\in[1,6]$。

然后是这个样子：

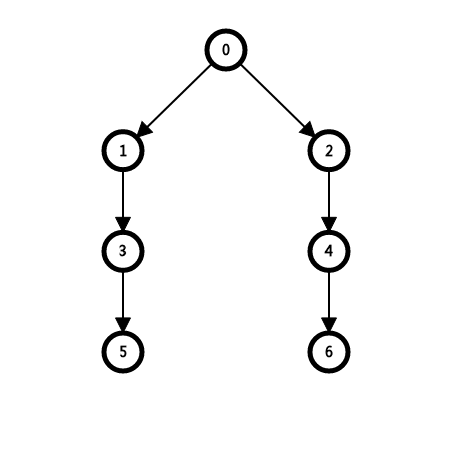
长度为 $4$ 和长度为 $6$ 的后缀的最长公共 border 长为 $2$，在树上的关系是什么？

可以看出，$2$ 是 $4$ 和 $6$ 除了自己之外的 LCA。

这棵树也就是所谓的失配树，通过对于一个字符串建出这棵树，我们可以快速找出其多组长度不同的前缀的最长公共 border 长度。

解释一下原理：

如果 $C$ 是 $B$ 的 border，$B$ 是 $A$ 的 border，那么 $C$ 是 $A$ 的 border。

也就是说处理出 $\text{nxt}$ 数组之后，$A$ 可以不断跳 $\text{nxt}$ 到 $B$，$B$ 也可以不断跳 $\text{nxt}$ 到 $C$。

所以说，如果两个前缀能通过跳 $\text{nxt}$ 跳到同一个位置去，那么第一个跳到的相同的位置就是它们的最长公共 border 长度。

这个过程和我们树上找 LCA 的方式很像，所以我们可以将其建成一棵树。

然后可以选择倍增或树剖等其他方式来跳。

我写了树剖求 LCA 结果 TLE 了，于是改了倍增，代码如下：

#include<queue>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 1000100
#define rr register 
#define INF 0x3f3f3f3f
//#define int long long

using namespace std;

char s[maxn];
int m,n,j,tot,f[maxn][40];
int nxt[maxn],head[maxn],dep[maxn];
struct edge{int fr,to,nxt;}e[maxn];

int read(){
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
    return s*w;
}

void add(int fr,int to){
    e[++tot]=(edge){fr,to,head[fr]};head[fr]=tot;
}

int dfs(int u){
    for(rr int i=1;i<=21;i++)
        f[u][i]=f[f[u][i-1]][i-1];
    for(rr int i=head[u];i;i=e[i].nxt){
        int to=e[i].to;
        dep[to]=dep[u]+1,f[to][0]=u;
        dfs(to);
    }
}

int GetLCA(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(rr int i=21;i>=0;i--)
        if(dep[f[x][i]]>=dep[y])x=f[x][i]; 
    for(rr int i=21;i>=0;i--)
        if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];    
    return f[x][0];
}

int main(){
    scanf("%s",s+1);n=strlen(s+1);
    for(rr int i=1;i<n;i++){
        while(j&&s[j+1]!=s[i+1]) j=nxt[j];
        if(s[j+1]==s[i+1]) j++,nxt[i+1]=j;
    }
    for(rr int i=1;i<=n;i++) add(nxt[i],i);
    dfs(0);m=read();
    for(rr int i=1,fr,to;i<=m;i++){
        fr=read();to=read();
        printf("%d\n",GetLCA(fr,to));
    }
    return 0;
}

我原以为树剖求 LCA 会超时是因为跳的太慢被卡了，后来发现不是的。

经过 @Suzt_ilymtics 大佬的研究发现，因为我们建出来的失配树根节点一定是 $0$，而我们的 $\text{son}$ 初值是 $0$，也就相当于所有点的重儿子一开始都是根节点，显然不对。

另外 $\text{siz}[0]$ 可能是很大的，可能导致剖分时找不到重儿子。所以我们将 $\text{son}$ 的初值设为一个大于 $n$ 的值就可以避免那种情况。

结果改完后实测比倍增快了 8s+。我就知道我树剖不会被卡。

树剖的代码

#include<queue>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 1000100
#define rr register 
#define INF 0x3f3f3f3f
//#define int long long

using namespace std;

char s[maxn];
int m,n,j,tot;
int nxt[maxn],head[maxn];
struct edge{int fr,to,nxt;}e[maxn];

int read(){
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
    return s*w;
}

void add(int fr,int to){
    e[++tot]=(edge){fr,to,head[fr]};head[fr]=tot;
}

namespace Cut{
    int siz[maxn],dep[maxn];
    int fa[maxn],son[maxn],top[maxn];
    void dfs1(int u,int fat){
        dep[u]=dep[fat]+1;
        siz[u]=1;fa[u]=fat;
        for(rr int i=head[u];i;i=e[i].nxt){
            int to=e[i].to;
            if(to==fat) continue;
            dfs1(to,u);siz[u]+=siz[to];
            if(siz[son[u]]<siz[to]) son[u]=to;
        }
    } 
    
    void dfs2(int u,int tp){
        top[u]=tp;
        if(son[u]!=n+5) dfs2(son[u],tp);//this.
        for(rr int i=head[u];i;i=e[i].nxt){
            int to=e[i].to;
            if(to==son[u]||to==fa[u]) continue;
            dfs2(to,to);
        }
    }
    
    int GetLCA(int x,int y){
        int fir=x,sec=y,ans;
        while(top[x]!=top[y]){
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            x=fa[top[x]];
        }
        ans=dep[x]<dep[y]?x:y;
        if(ans==fir||ans==sec) return fa[ans];
    }
}

int main(){
    scanf("%s",s+1);n=strlen(s+1);
    for(rr int i=1;i<n;i++){
        while(j&&s[j+1]!=s[i+1]) j=nxt[j];
        if(s[j+1]==s[i+1]) j++,nxt[i+1]=j;
    }
    for(rr int i=0;i<=n;i++) Cut::son[i]=n+5;//and this.
    for(rr int i=1;i<=n;i++) add(nxt[i],i);
    Cut::dfs1(0,-1);Cut::dfs2(0,0);
    
    m=read();
    for(rr int i=1,fr,to;i<=m;i++){
        fr=read();to=read();
        printf("%d\n",Cut::GetLCA(fr,to));
    }
    return 0;
}