洛谷P2292

在《信息学奥赛一本通提高篇》中 Trie字典树 的课后练习看到这道题
然后我就用 Trie字典树 做了这道题
听说这道题的正解是 AC自动机，数据跑满时其他的算法都可以卡掉
然而数据没那么强，我终究是过了

Description

给定 \(n\) 个词汇，\(m\) 个语句，每个语句由若干个词汇连续构成，每个词汇由若干个字符连续构成
对于一个词汇，当且仅当这个词汇能被完整的识别，也就是属于给定的词汇中的一个时，我们称 已理解此词汇
对于一个语句，当且仅当其中的任意一个词汇之前的所有词汇都已被理解时，才可以开始识别此词汇
现在对于每个语句，要求输出其最后一个能被理解的词汇的末尾位置的下标

Solution

这里讲一下如何用踹树去做这道题
首先看样例

4 3 
is
name
what
your
whatisyourname
whatisyouname
whaisyourname

这是给定的词汇和语句，思考一下该如何去从头识别每一个语句中的词汇
根据踹树的原理可知，我们可以以每个给定词汇为一个分支，以每个字符作为转移条件，建一棵踹树
具体如图所示：

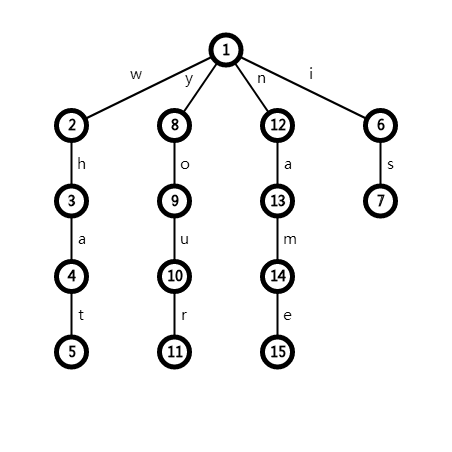
每次从根节点开始向下遍历，每理解一个词汇计数器就更新
若遍历出错，则直接返回答案
若已遍历到叶节点显示还未出错，则返回根节点找下一个词汇，直到出错或者整个语句已全部被理解
然后就可以极慢地找出每个语句能被理解到的最末位置

在此基础上，我们维护两个 \(map\)，一个记录当前语句是否被理解过，另一个统计当前语句能被理解到的最末位置
原因是在某些情况下，同样的运算步骤可能会重复很多遍，但使用映射 \(map\) 就可以解决这个问题，相当于递归时的记忆化
当第一个 \(map\) 显示当前语句已被理解过时，直接用另一个 \(map\) 输出对应的最末位置，可以避免再重新识别当前这个已经被理解过一次的语句
这样就可以使得这个时间复杂度非常差的做法稍微快一点

Other things

以上显然是一个暴力的做法，纯属乱搞
然而踹树本身就不是本题的正解，如果能过那就是因为数据过水
本着尊重《信息学奥赛一本通提高篇》的编者的原则，我才用他所指定的这个做法来做这道题
至于这道题的正解 AC自动机
我不会 蛤蛤

Code

#include<map>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 200010
#define LL long long
#define uLL unsigned long long

using namespace std;

int n,m,ans;
char s[25],S[maxn];
map<string,int> Get;
map<string,bool> Judge;

inline int read(){
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();
    return s*w;
}

struct Trie{
    int Nxt[maxn][25],cnt;
    bool flag[maxn],vis[maxn];
    void Insert(char *s){
	int p=0,len=strlen(s+1);
	for(int i=1;i<=len;i++){
	    int c=s[i]-'a';	
	    if(!Nxt[p][c]) Nxt[p][c]=++cnt;
   	        p=Nxt[p][c];
	}
	flag[p]=1;
    }
	
    int Find(char *s){
	int p=0,len=strlen(s+1);
	if(Judge[s+1]) return Get[s+1];
	memset(vis,false,sizeof vis);vis[0]=true;
	for(int i=0;i<=len;i++){
	    if(!vis[i]) continue;cnt=i;
	    for(int j=i+1;j<=len;j++){
	        int c=s[j]-'a';
		p=Nxt[p][c];if(!p) break;
	        if(flag[p]) vis[j]=true;
	    }
	}
	Judge[s+1]=true;Get[s+1]=cnt;
	return cnt;
    }
}Tri;

int main(){
    n=read();m=read();
    for(int i=1;i<=n;i++){
	scanf("%s",s+1);
	Tri.Insert(s);
    }
    for(int i=1;i<=m;i++){
	scanf("%s",S+1);
	printf("%d\n",Tri.Find(S));
    }
    return 0;
}