acm22纳新题题解:D.喜子哥开空调

喜子哥开空调

Description

喜子掌管着工作室的空调遥控器, 他可以自由调整室内的温度, （这么牛？！我咋不信。。）但每个人最喜欢的室内温度不都相同, 如果当前室温k与自身适应的温度a[i]的差值没超过忍耐限度p, (即 | a[i]-k | ≤ p)那么这个小伙伴就能够正常训练, 否则就会变得十分烦躁无心做题。

现在已知有n名队员在工作室里训练, 身为工作室集训的头儿, 喜子哥想知道, 在最佳情况下, 最多有多少队员能够同时正常训练

Input

第一行两个数n,p(1≤n,p≤1000000),n:队员数量, p:题意中的忍耐限度

接下来每行有n个数ai表示每名队员最适应的温度

Output

输出一个数字, 表示最多有多少队员同时正常训练

Sample Input 1

6 2
1 5 3 2 4 6

Sample Output 1

5

温度调成3或4，都可以满足5名队员同时正常训练
通过对题意的分析,
我们需要找到最多的正常训练人数,
也就是说找到一个温度区间[k-p, k+p],使得在这个区间里的人最多

1. 我这里搞了个cnt[]数组, Ⅰ.cnt[x]初始化为表示喜欢x的人数
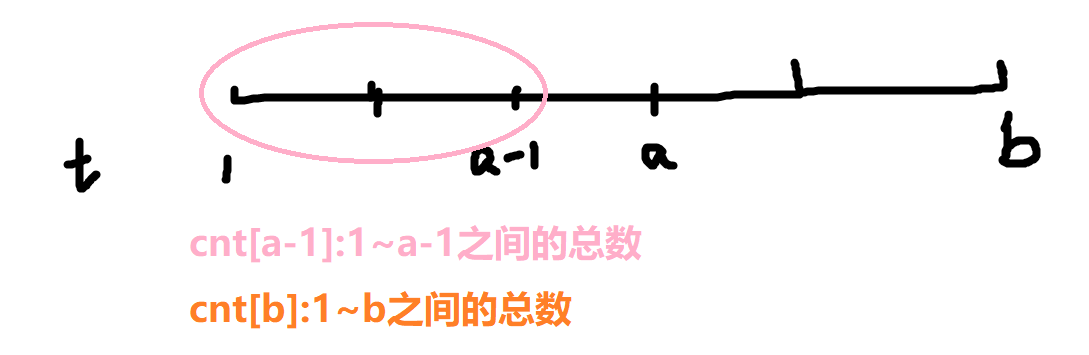
2. 然后用到了前缀和的思想(可以去了解一下), 利用前缀和可以快速求得某段区间的总和,Ⅱ.经过处理后cnt[x](x为正整数)可以表示区间[1,x]之间的人数和, 例如下图

那么cnt[b]-cnt[a]就可以表示区间cnt[a]~cnt[b]之间的总数

c++写法(c语言同理,只是输入输出换成printf/scanf的写法)

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e4;
int cnt[N],s[N];
int main()
{
    int n,p,res=0;
    cin>>n>>p;
    
    int x;
	//Ⅰ.cnt[x]初始化为表示喜欢x的人数
    for(int i = 0 ; i < n; i++){
        scanf("%d",&x);
        cnt[x] ++;
    }
	//Ⅱ.经过处理后cnt[x]可以表示区间[1,x]之间的人数和
    for(int i = 1 ; i <= n; i++){
        cnt[i] += cnt[i-1];
    }
	//枚举1~n之间的每个温度
    for(int i = 1 ; i <= n; i++){
		//注意i+p不能超过n, i-p-1不能比0小
		//为什么是i-p还要减一呢,因为我们想求[i-p,i+p]之间的总和
		//就像上面的图里的a一样, 需要减一
        int t = cnt[min(n, i+p)] - cnt[max(0,i-p-1)];//求区间和
		//更新res
        if(res < t) res = t;
    }
    cout << res;
}