多元函数中的连续, 可微, 与可偏导

在多元函数中

• 可微, 指全微分存在
• 可导, 指偏导数存在

全微分可以表示为：

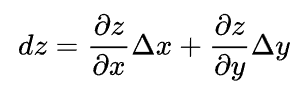
与切平面方程对比：

$$f_x(x_0, y_0)(x - x_0)+f_y(x_0, y_0)(y - y_0)-(z - z_0)=0$$

可以清晰地看到，假设A点（x0,y0）与B点（x,y）向上作两条垂线与切平面相交M，N两点，其高度分部是z0和z,再将(z-z0)看作是dz,那么全微分就是M,N两点之间的高度差，也就是说，全微分就代表切平面上两点的高度差，如下图：

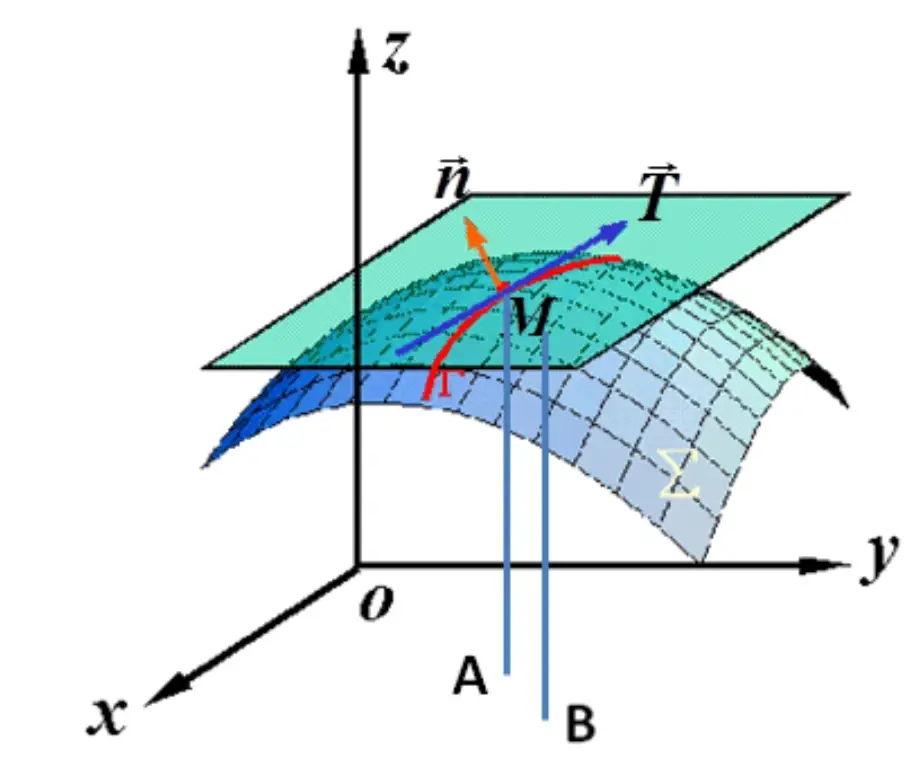
由以上分析，那么微分存在的前提就是切平面存在，而切平面存在就要求曲面上这一点每个方向的偏导数存在，如下图所示：

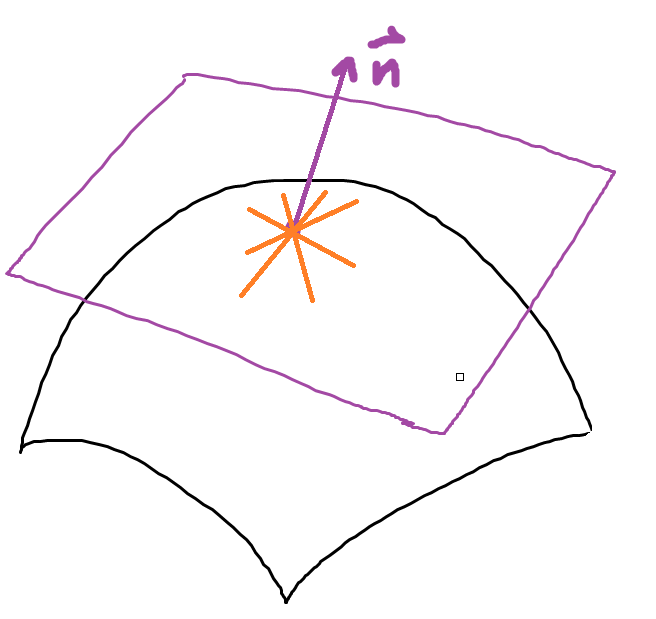
如上图，结合二元函数的几何意义，切平面存在，必须要曲面上通过该点任何方向的曲线都具有切线，且这些切线都在同一个平面（切平面）上。也就是曲面上这一点的偏导数连续，也就是只有当偏导数连续的时候才能保证微分存在。

但是反过来，微分存在是不是一定要求偏导数连续呢？

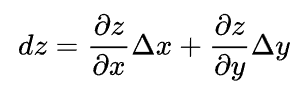
由上式，只要x,y轴两个方向的偏导数在某一点存在的时候，微分就存在，所以由微分存在无法保证其它方向的偏导数存在，也就是无法保证偏导数连续，如下图。只要曲面上的某点x，y两个方向的偏导数存在就是可导。

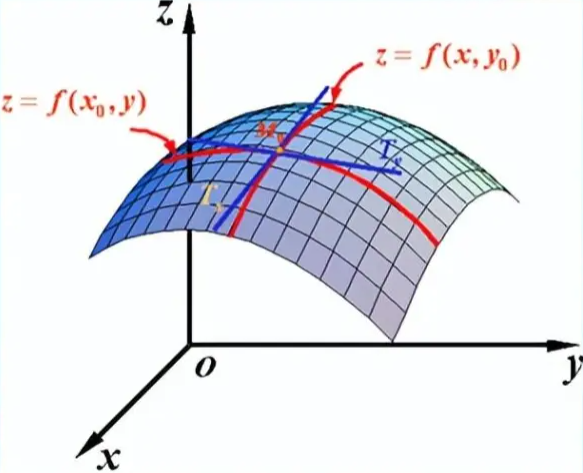
偏导数的几何意义：

偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率；
偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。

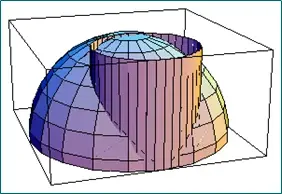
上图的球面和柱面交界处，偏导数肯定不连续。

所以：

1. 当偏导数连续的时候，表示切平面存在，从而函数可微。
2. 但反过来，可微不一定能推出偏导数连续。