2023蓝桥省赛赛前准备

目录

• unordered_set
• priority_queue
• 并查集
• *二分
• 数学
  • 快速幂
  • 找末尾1
  • 质数
    • 试除法分解质因数
    • 试除法判断质数
    • 朴素筛求质数
    • *线性筛求质数
  • 约数
    • 最大公约数
    • 试除法求约数
• 图论
  • 拓扑排序
  • 最短路
    • 朴素Dijkstra
    • 堆优化Dijkstra
    • Bellman-Ford
    • Floyd
  • 最小生成树
    • prim
    • kruskal
• 其他
  • 判断闰年
  • 储存单位转换

unordered_set

unordered_set::size | Microsoft Learn

#include <unordered_set>

unordered_set<T> st;
T tmp;
st.insert(tmp);
st.empty() //false
if(st.count(tmp)){
    //✔
}

st.clear();
st.empty() //true

priority_queue

priority_queue::priority_queue | Microsoft Learn

//升序队列，小顶堆
priority<int, vector<int>, greater<int>> heap;
priority<PII, vector<PII>, greater<PII>> heap;

// 默认大顶堆
priority_queue<int> a; 
priority_queue<int, vector<int>, less<int>> a; 

heap.push({0, 1});
auto t = heap.top();
heap.pop();

并查集

int find(int x){
    if(f[x] != x) f[x] = find(f[x]);
    return f[x];
}

for(int i = 1; i <= n; ++i) f[i] = i;

//合并集合
f[find(a)] = find(b); 

*二分

NC235558 牛可乐和魔法封印

#include<iostream>
using namespace std;

const int N = 1e5+10;
int a[N], n, q;

//找到大于等于x的第一个数下标
int find_l(int x){ 
    int l = 1, r = n;
    while(l < r){
        int mid = (l + r) >> 1;
        if(a[mid] >= x) r = mid;
        else l = mid+1;
    }
    return l;
}
//找到小于等于x的第一个数下标
int find_r(int x){
    int l = 1, r = n;
    while(l < r){
        int mid = (l + r + 1) >> 1;
        if(a[mid] <= x) l = mid;
        else r = mid-1;
    }
    return r;
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    scanf("%d", &q);
    
    int l, r;
    while(q --)
    {
        scanf("%d%d", &l, &r);
        if(l > a[n] || r < a[1]) puts("0");
        else printf("%d\n", find_r(r)-find_l(l)+1);
    }
    return 0;
}

蓝桥杯十大常见天阶功法——虫之呼吸.贰之型.二分

数学

快速幂

// 求x^n mod p
LL quick_power(int x, int n, int p){
    LL res = 1;
    while(n){
        if(n & 1) res = res*(LL)x%p;
        x = x*(LL)x%p;
        n >>= 1;
    }
    return res;
}

找末尾1

int lowbit(int x){
    return x & -x;
}

质数

试除法分解质因数

void divide_prime(int n){
    for(int i = 2; i <= x/i; ++i){
        if(x % i == 0){
            int cnt = 0;
            while(x % i == 0) x /= i, ++cnt;
            cout << i << " " << cnt << endl;
        }
    }
    
    if(x > 1) cout << x << " " << 1 << endl;
    cout << endl;
}

试除法判断质数

bool is_prime(int x){
    if(x < 2) return false;
    for(int i = 2; i <= x/i; ++i)
        if(n % i == 0)
            return false;
    return true;
}

朴素筛求质数

int primes[N], cnt;
bool st[N];
void get_primes(int x){
    int cnt = 0;
    for(int i = 2; i <= x; ++i){
        if(!st[i]){
            primes[cnt++] = i;
            for(int j = i+i; j <= x; j += i) st[j] = true;
        }
    }
}

*线性筛求质数

int primes[N], cnt;
bool st[N];
void get_primes(int x){
    for(int i = 2; i <= x; ++i){
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; primes[j] <= x / i; ++j){
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}

约数

最大公约数

int gcd(int a, int b){
    return b ? gcd(b, a % b) : a;
}

试除法求约数

vector<int> get_divisor(int x){
    vector<int> res;
    for(int i = 1; i <= x / i; ++i)
        if(x % i == 0){
            res.push_back(i);
            if(i != x / i) res.push_back(x / i);
        }
        
    sort(res.begin(), res.end());
    return res;
}

图论

拓扑排序

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5+10;
int n, m;
int in[N], q[N];
int e[N], h[N], ne[N], idx;

void add(int a, int b){
    e[idx] = b, in[b]++, ne[idx] = h[a], h[a] = idx++;
}

int topSort()
{
    int front = -1, rear = -1;
    for(int i = 1; i <= n; ++i)
        if(!in[i])
            q[++rear] = i;
            
    while(front != rear)
    {
        int t = q[++front];
        
        for(int i = h[t]; ~i; i = ne[i]){
            int x = e[i];
            --in[x];
            if(!in[x]) q[++rear] = x;
        }
    }
    return rear == n-1;
}

int main()
{
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    int a, b;
    for(int i = 0; i < m; ++i){
        cin >> a >> b;
        add(a, b);
    }
    
    if(topSort()){
        for(int i = 0; i < n; ++i) cout << q[i] << " ";
    }else printf("-1");
    
    return 0;
}

最短路

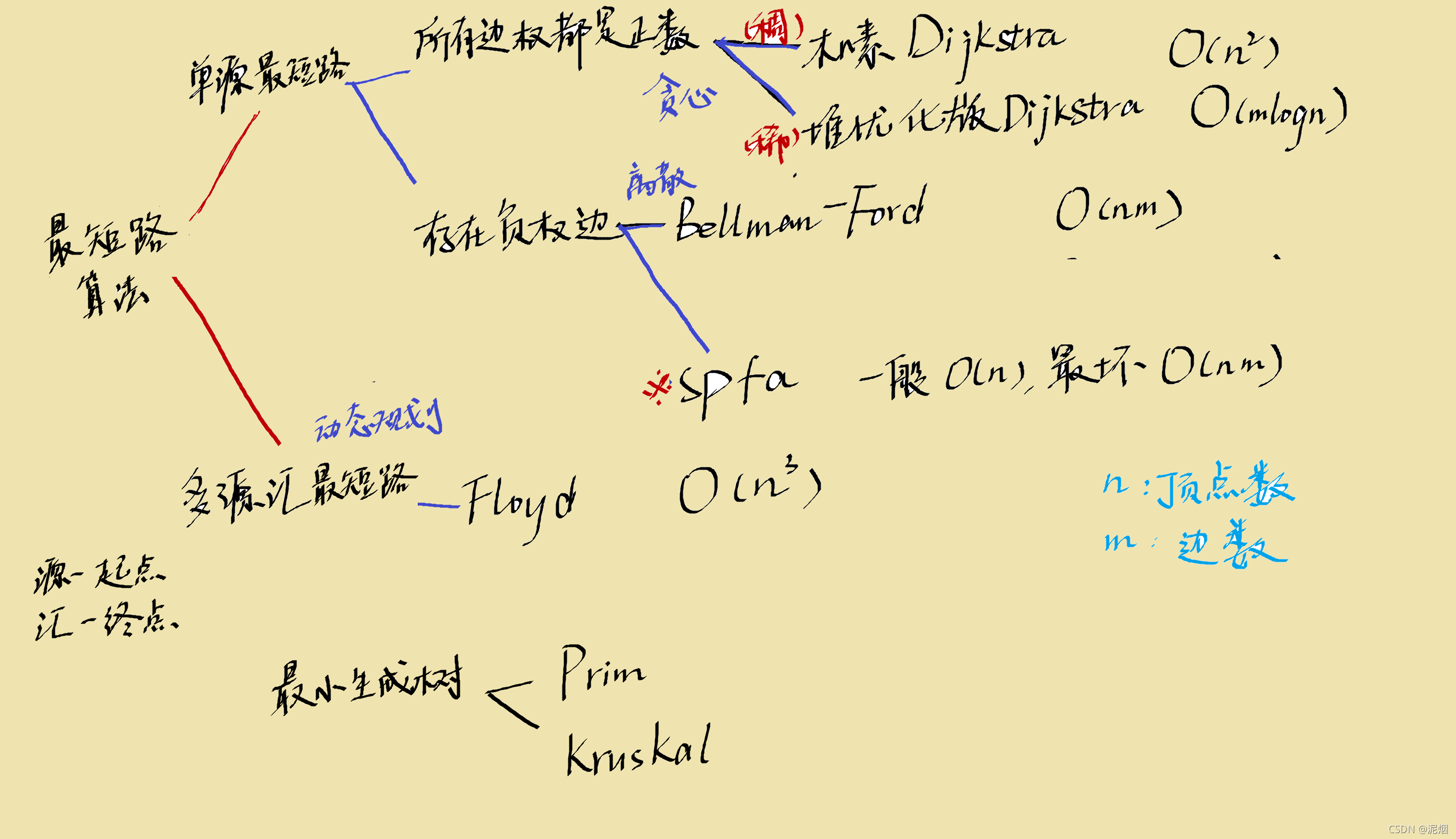
朴素Dijkstra

如: 求 1->n 的最短路

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510;
int n, m;
bool st[N];
int g[N][N], d[N];

int dijkstra(){
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    
    for(int i = 0; i < n; ++i)
    {
        int t = -1;
        for(int j = 1; j <= n; ++j)
            if(!st[j] && (t == -1 || d[j] < d[t]))
                t = j;
        
        if(t == n) break;
        st[t] = true;
        for(int j = 1; j <= n; ++j)
            if(!st[j]) d[j] = min(d[j], d[t]+g[t][j]);  
    }
    
    if(d[n] == 0x3f3f3f3f) return -1;
    else return d[n];
}

int main()
{
    scanf("%d%d", &n, &m);
    
    memset(g, 0x3f, sizeof g);
    
    int a, b, c;
    for(int i = 0; i < m; ++i)
    {
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
    }
    
    printf("%d", dijkstra());
    return 0;
}

堆优化Dijkstra

#include <iostream>
#include <cstring>
#include <queue>
#define x first
#define y second
using namespace std;

typedef pair<int, int> PII;
const int N = 150010;
int n, m;
bool st[N];
int dist[N];
int e[N], ne[N], h[N], w[N], idx;

void add(int a, int b, int c){
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

int dij_treap()
{
    memset(dist, 0x3f, sizeof dist);
    priority_queue<PII, vector<PII>, greater<PII>> q;
    q.push({0, 1});
    dist[1] = 0;
    
    while(!q.empty())
    {
        auto t = q.top();
        q.pop();
        int dis = t.x, ver = t.second;
        
        if(st[ver]) continue ;
        st[ver] = true;
        
        for(int i = h[ver]; ~i; i = ne[i])
        {
            int u = e[i];
            if(dist[u] > dis + w[i]){
                dist[u] = dis + w[i];
                q.push({dist[u], u});
            }
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    
    int a, b, c;
    while (m -- )
    {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    
    cout << dij_treap();
    return 0;
}

Bellman-Ford

Floyd

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, k;
int d[N][N];

void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
    cin >> n >> m >> k;
	
    //初始化
    memset(d, 0x3f, sizeof d);
    for (int i = 1; i <= n; i ++ ) d[i][i] = 0;

    int a, b, c;
    while (m -- )
    {
        scanf("%d%d%d", &a, &b, &c);
        d[a][b] = min(d[a][b], c);
    }

    floyd();
    while (k --)
    {
        scanf("%d%d", &a, &b);

        int res = d[a][b];
        if (res > INF / 2) //★
            cout << "impossible" << '\n';
        else cout << res << '\n';
    }

    return 0;
}

最小生成树

prim

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510, M = 1e5+10, INF = 0x3f3f3f3f;
int n, m;
bool st[N];
int g[N][N], d[N];

int prim(){
    memset(d, INF, sizeof d);
    d[1] = 0;
    int res = 0;

    for(int i = 0; i < n; ++i)
    {
        int t = -1;
        for(int j = 1; j <= n; ++j)
            if(!st[j] && (t == -1 || d[j] < d[t]))
                t = j;

        if(i && d[t] == INF) return INF;
        if(i) res += d[t];
        st[t] = true;

        for(int j = 1; j <= n; ++j)
            d[j] = min(d[j], g[t][j]);
    }

    return res;
}
int main()
{
    memset(g, INF, sizeof g);
    scanf("%d%d", &n, &m);

    int a, b, c;
    while (m -- )
    {
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    int res = prim();
    if(res != INF) cout << res;
    else cout << "impossible";
    return 0;
}

kruskal

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 2e5+10, INF = 0x3f3f3f3f;
int n, m;
int f[N];
struct Edge{
    int a, b, w;
    bool operator < (const Edge& e)const{
        return w < e.w;
    }
}e[N];

int find(int x){
    if(f[x] != x) f[x] = find(f[x]);
    return f[x];
}

int kruskal()
{
    sort(e, e + m);
    if(e[0].w == INF) return INF;

    for(int i = 1; i <= n; ++i) f[i] = i;

    int res = 0, cnt = 0;
    for(int i = 0; i < m; ++i)
    {
        int fa = find(e[i].a), fb = find(e[i].b);
        if(fa != fb){
            f[fb] = fa;
            res += e[i].w;
            cnt ++;
        }
    }

    if(cnt != n-1) return INF;
    else return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    int a, b, w;
    for(int i = 0; i < m; ++i)
    {
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }

    int res = kruskal();
    if(res == INF) cout << "impossible";
    else cout << res;
    return 0;
}

其他

判断闰年

if(year % 400 == 0 || (year % 100 != 0 && year % 4 == 0)){
    return true;
}else return false;

储存单位转换

1MB=1024KB=1048576字节

1G=1024M=1048576KB

1TB=1024GB

1GB=1024MB

1MB=1024KB

1KB=1024Byte

1Byte=8bit