[总结] 高等数学的一些理解
🚝
目录
极限
"什么情况下求极限可以直接带入"
- 随意等价替换的问题

- 随意代入值的问题

- 隐含四则运算

"关于等价无穷小使用条件问题"

- 我们会发现分母是一个对精确度要求的明显指标——分母数量级越小,对分子的变化越敏感(想想反比例函数在0
点的性态),于是对估值的精度要求变高.- 上下同阶原理
"如何解释洛必达法则(一阶泰勒展开)"
有关泰勒展开
常用
导数与微分
※导数极限定理、分段点求导能不能用公式?导数和导数的极限?
高数 | 导数极限定理、分段点求导能不能用公式?导数和导数的极限?
"二阶导数的记号为何如此怪异"
[○]数列极限问题
积分
含三角函数的积分的一些常用结论
积不出来的(原函数不初等)

变限积分
https://zhuanlan.zhihu.com/p/425569861
1.变上限积分与原函数有什么关系?
2.分段函数的变上限积分如何求?
3.变上限积分在被积函数第一类间断点处如何(连续or可导?)
微分方程
线性微分方程与非线性微分方程
微分方程与线性代数
微积分基本定理
多元函数
[○]全微分形式的不变性
极值的判定,如何理解充分条件
多元函数中,为什么 AC-B² 可以判定极值?AC-B² 这个判别式是怎么来的?
求极坐标二重积分时,为什么要乘上ρ?

级数
幂级数逐项积分和求导后的收敛性分析




由上面的定理和推论可知,幂级数逐项积分和逐项求导后所得的幂级数都与原级数的收敛半径相同,但收敛域可能不同,它们之间的关系是:逐项积分后所得幂级数的收敛域包含原幂级数的收敛域,而逐项求导所得幂级数的收敛域被包含于原幂级数的收敛域之内。从上面的例题中我们也看到了,三者之间可能是不相同的
本文来自博客园,作者:泥烟,CSDN同名, 转载请注明原文链接:https://www.cnblogs.com/Knight02/p/17195513.html





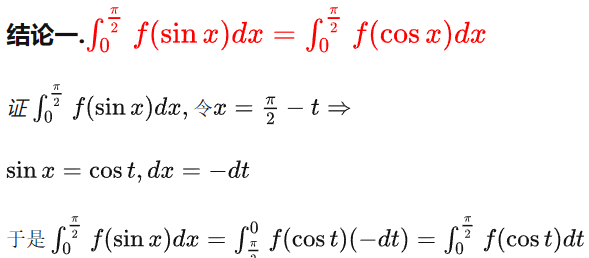


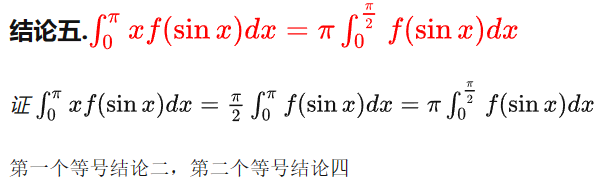


 浙公网安备 33010602011771号
浙公网安备 33010602011771号