C++实现Trie 树

目录

数组实现

本质

一种优化方法

代码实现

适用场景

---

 

---

数组实现

之前做题用数组模拟过Trie树的实现: 

[图解] 数组模拟Trie树_☆迷茫狗子的秘密基地☆-CSDN博客https://blog.csdn.net/qq_39391544/article/details/120775174?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163824589916780357224643%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=163824589916780357224643&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_v29-1-120775174.pc_v2_rank_blog_default&utm_term=trie&spm=1018.2226.3001.4450

本质

Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起

主要有两个操作，

一个是将字符串集合构造成 Trie 树

另一个是在 Trie 树中查询一个字符串

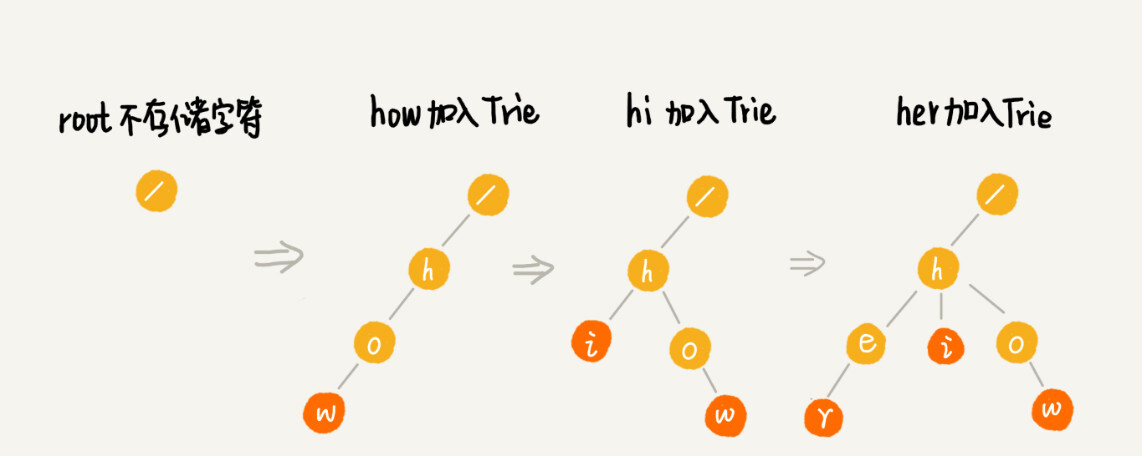
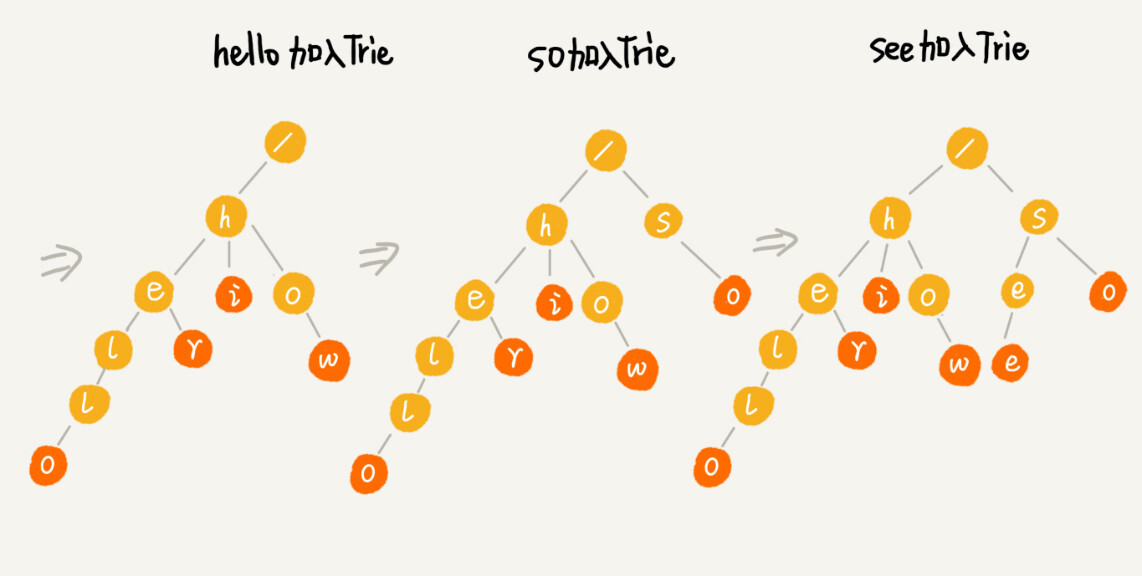
 Trie 树的本质是避免重复存储一组字符串的相同前缀子串，但是现在每个字符（对应一个节点）的存储远远大于 1 个字节

我们不可否认，Trie 树可能很浪费内存，但是确实非常高效。

我们也可以稍微牺牲一点查询的效率，将每个节点中的数组换成其他数据结构，比如有序数组、跳表、散列表、红黑树等, 来存储一个节点的子节点指针。

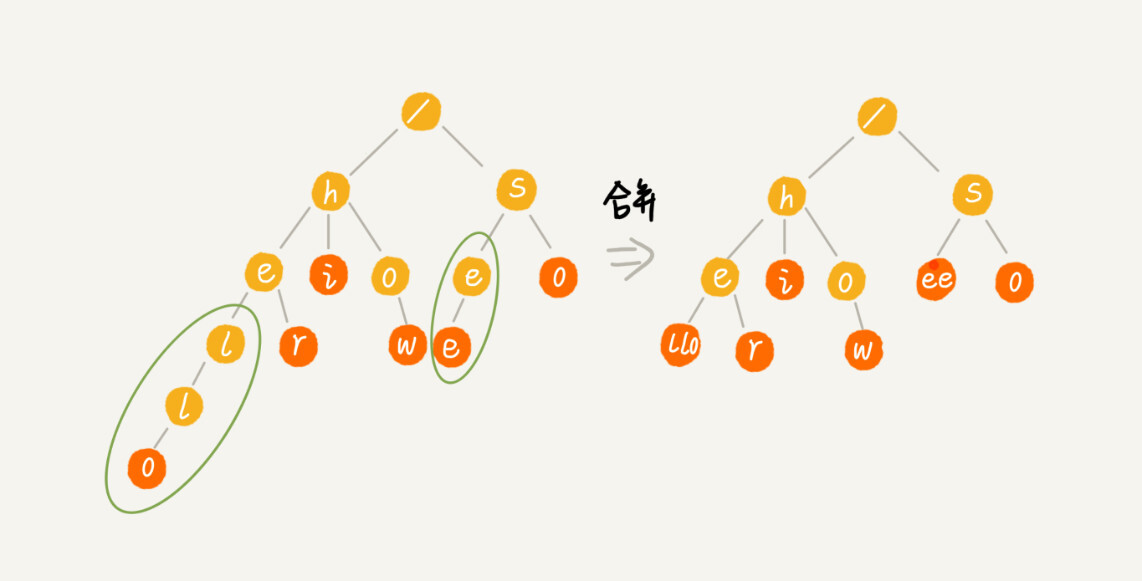
一种优化方法

缩点优化，就是对只有一个子节点的节点，而且此节点不是一个串的结束节点，可以将此节点与子节点合并。这样可以节省空间，但却增加了编码难度

代码实现

#include<iostream>
#include<cstring>
#define Size 26
using namespace std;

template<typename T> 
struct TrieNode{
    T data;
    bool isEnd;	//是否为词尾 
    TrieNode* child[Size];
    
    TrieNode(T ch):data(ch),isEnd(false){
		for(int i = 0; i < Size; i ++) {
			child[i] = NULL;
		}	
	}
};

class Trie
{
	private:
	    TrieNode<char>* root;
	    int num;
	public:
	    Trie();
	    void Insert(string s);
	    bool Search(string s);
};

Trie::Trie()
{
    root = new TrieNode<char>('#');
}

void Trie::Insert(string s)
{
    TrieNode<char>* p = root;
    int size = s.length();
    for(int i = 0; i < size; i ++)
    {
        int index = s[i] - 'a';
        if(p->child[index] == NULL){
            p->child[index] = new TrieNode<char>(s[i]);
        }
        p = p->child[index];
    }
    p->isEnd = true; //标记为词尾 
    cout << "sucess insert \"" << s << "\"" << endl;

}
bool Trie::Search(string s)
{
    TrieNode<char>* p = root;
    int size = s.length();
    for(int i = 0; i < size; i ++)
    {
        int index = s[i] - 'a';
        if(p->child[index] == NULL){
            return false;
        }
        p = p->child[index];
    }
    // 可能不存在该单词,只是一段前缀 
    if(p->isEnd) return true;
    else return false;
}

int main()
{
	Trie tree;

	// 测试 
	string s[] = {"he", "hello", "app", "apple", "application", "book", "boom"};
	
    tree.Insert(s[0]);
	tree.Insert(s[1]);
	tree.Insert(s[3]);
	tree.Insert(s[5]);
    for(auto t : s){
    	if(tree.Search(t))   cout << t << " 已找到" << endl;
		else  cout << t << " 未找到" << endl;
        
    }
	return 0;
}

 

适用场景

Trie对要处理的字符串有较高的要求。

1. 字符串中包含的字符集不能太大且要求字符串的前缀重合比较多。否则，存储空间可能会浪费很多。即便可以优化，也要付出牺牲一部分效率的代价
2. 要自己从零开始实现一个 Trie 树，还要保证没有 bug，这在工程上是将简单问题复杂化，除非必须，一般不建议
3. 指针串起来的数据块是不连续的，所以，对缓存并不友好，性能上会打折扣

综上倾向于用散列表或者红黑树,有相应的类库

而Trie 树的特点使她可以应用到自动输入补全，如输入法自动补全、IDE 代码自动补全功能、浏览器网址输入时的自动补全功能等