[牛客每日一题] (单调队列) NC50528 滑动窗口
滑动窗口 (nowcoder.com)![]() https://ac.nowcoder.com/acm/problem/50528
https://ac.nowcoder.com/acm/problem/50528
题目描述
给一个长度为N的数组,一个长为K的滑动窗体从最左端移至最右端,你只能看到窗口中的K个数,每次窗体向右移动一位,如下图:
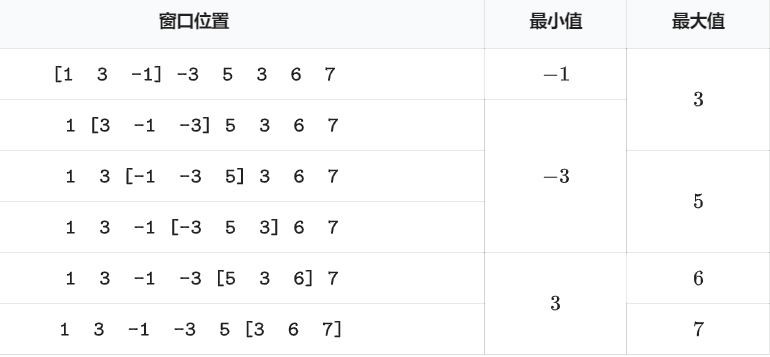
你的任务是找出窗体在各个位置时的最大值和最小值。
输入描述:
第1行:两个整数N和K; 第2行:N个整数,表示数组的N个元素(≤2×10^9);
输出描述:
第一行为滑动窗口从左向右移动到每个位置时的最小值,每个数之间用一个空格分开; 第二行为滑动窗口从左向右移动到每个位置时的最大值,每个数之间用一个空格分开。
示例1
输入
8 3 1 3 -1 -3 5 3 6 7
输出
-1 -3 -3 -3 3 3 3 3 5 5 6 7
备注:
对于20%的数据,K≤N≤1000; 对于50%的数据,K≤N≤10^5; 对于100%的数据, K≤N≤10^6。
以最大值举例,

可见中间的从a[l+1]到a[r]为共用区间, 不同之处只有a[l]和a[r+1],
使用单调队列, 保证当前队列的第一位一定是当前区间的最大值,
当a[i]>a[i-1], 即a[i-1]的辉煌不已再(它可能之前当过老大,但出现更强的元素时他就再也无法出现在我们的视线中), a[i]之前的所有比a[i]小的都会被舍弃, 以此大幅减少了我们求最值时重复的工作量
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e6+10;
int a[N],q[N];
int main()
{
int n, k;
cin >> n >> k;
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
int front = 0, rear = -1;
for(int i = 1; i <= n; i ++)
{
//去除闲杂元素
if(front <= rear && i-k+1 > q[front]) front++;
//优胜劣汰
while(front <= rear && a[i] < a[q[rear]]) rear--;
q[++rear] = i;
if(i >= k) printf("%d ", a[q[front]]);
}
cout << endl;
front = 0, rear = -1;
for(int i = 1; i <= n; i ++)
{
if(front <= rear && i-k+1 > q[front]) front++;
while(front <= rear && a[i] >= a[q[rear]]) rear--;
q[++rear] = i;
if(i >= k) printf("%d ", a[q[front]]);
}
return 0;
}本文来自博客园,作者:泥烟,CSDN同名, 转载请注明原文链接:https://www.cnblogs.com/Knight02/p/15799002.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号