AcWing2022寒假每日一题(1 月 2 日 ~ 1 月 6 日)
目录
1/2 AcWing 2058. 笨拙的手指

输入样例:
1010
212
输出样例:
14
样例解释
14 在二进制下的正确表示为 1110,在三进制下的正确表示为 112。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
//秦九韶算法, k进制转十进制
int trans(string s, int k)
{
int res = 0;
int len = s.length();
for(int i = 0; i < len; i ++) res = res*k+s[i]-'0';
return res;
}
int main()
{
unordered_set<int> s;
string a, b;
cin >> a >> b;
for(auto& c: a){
c ^= 1; //48->49 49->48
s.insert(trans(a, 2));
c ^= 1;
}
for(auto& c: b){
char st = c;
for(int i = 0; i < 3; i ++){
if(i+'0'!=c){
c = i+'0';
int x = trans(b, 3);
if(s.count(x)){
cout << x << endl;
return 0;
}else{
s.insert(x);
}
}
c = st;
}
}
return 0;
}1/3 AcWing 2041. 干草堆

输入样例:
7 4
5 5
2 4
4 6
3 5
输出样例:
1
样例解释
贝茜完成所有指令后,各堆高度为 0,1,2,3,3,1,0。
将各高度从小到大排序后,得到 0,0,1,1,2,3,3,位于中间的是 1。
前缀和
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6+10;
int s[N],a[N];
int main()
{
int n,t;
cin >> n >> t;
while(t --)
{
int l ,r;
cin >> l >> r;
s[l]++;
s[r+1]--;
}
for(int i = 1; i <= n; i++) s[i]+=s[i-1];
sort(s+1, s+n+1);
cout << s[(1+n)>>1];
return 0;
}1/4 AcWing 2060. 奶牛选美
听说最近两斑点的奶牛最受欢迎,约翰立即购进了一批两斑点牛。
不幸的是,时尚潮流往往变化很快,当前最受欢迎的牛变成了一斑点牛。
约翰希望通过给每头奶牛涂色,使得它们身上的两个斑点能够合为一个斑点,让它们能够更加时尚。
牛皮可用一个 N×M 的字符矩阵来表示,如下所示:
................
..XXXX....XXX...
...XXXX....XX...
.XXXX......XXX..
........XXXXX...
.........XXX....
其中,X 表示斑点部分。
如果两个 X 在垂直或水平方向上相邻(对角相邻不算在内),则它们属于同一个斑点,由此看出上图中恰好有两个斑点。
约翰牛群里所有的牛都有两个斑点。
约翰希望通过使用油漆给奶牛尽可能少的区域内涂色,将两个斑点合为一个。
在上面的例子中,他只需要给三个 .. 区域内涂色即可(新涂色区域用 ∗∗ 表示):
................
..XXXX....XXX...
...XXXX*...XX...
.XXXX..**..XXX..
........XXXXX...
.........XXX....
请帮助约翰确定,为了使两个斑点合为一个,他需要涂色区域的最少数量。
输入格式
第一行包含两个整数 N 和 M。
接下来 NN 行,每行包含一个长度为 M 的由 X 和 . 构成的字符串,用来表示描述牛皮图案的字符矩阵。
输出格式
输出需要涂色区域的最少数量。
数据范围
1≤N,M≤50
输入样例:
6 16
................
..XXXX....XXX...
...XXXX....XX...
.XXXX......XXX..
........XXXXX...
.........XXX....
输出样例:
3数据范围较小, 可以dfs+暴力枚举, 取两区块之间最小曼哈顿距离
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 51;
typedef pair<int, int> PII;
int n, m;
char g[N][N];
vector<PII> v[2];
int dx[4]={0, 1, 0, -1}, dy[4]={1, 0, -1, 0};
void dfs(int x, int y, vector<PII>& u)
{
g[x][y] = '.';
u.push_back({x, y});
for(int i = 0; i < 4; i ++)
{
int nx=x+dx[i], ny=y+dy[i];
if(nx>=0 && nx<n && ny>=0 && ny<m && g[nx][ny]=='X') //周围所有X
dfs(nx, ny, u);
}
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++) cin >> g[i];
for(int i = 0, k = 0; i < n; i ++)
for(int j = 0; j < m; j++)
if(g[i][j] =='X') dfs(i, j, v[k++]);
int res = 1e9;
for(auto& a: v[0])
for(auto& b : v[1])
res = min(res, abs(a.first-b.first)+abs(a.second-b.second)-1);
cout << res;
return 0;
}1/5 AcWing 2019. 拖拉机
干了一整天的活,农夫约翰完全忘记了他把拖拉机落在田地中央了。
他的奶牛非常调皮,决定对约翰来场恶作剧。
她们在田地的不同地方放了 N 捆干草,这样一来,约翰想要开走拖拉机就必须先移除一些干草捆。
拖拉机的位置以及 N 捆干草的位置都是二维平面上的整数坐标点。
拖拉机的初始位置上没有干草捆。
当约翰驾驶拖拉机时,他只能沿平行于坐标轴的方向(北,南,东和西)移动拖拉机,并且拖拉机必须每次移动整数距离。
例如,驾驶拖拉机先向北移动 2单位长度,然后向东移动 3 单位长度。
拖拉机无法移动到干草捆占据的位置。
请帮助约翰确定他需要移除的干草捆的最小数量,以便他能够将拖拉机开到二维平面的原点。
输入格式
第一行包含三个整数:N 以及拖拉机的初始位置 (x,y)。
接下来 N 行,每行包含一个干草捆的位置坐标 (x,y)。
输出格式
输出约翰需要移除的干草捆的最小数量。
数据范围
1≤N≤50000,
1≤x,y≤1000
输入样例:
7 6 3
6 2
5 2
4 3
2 1
7 3
5 4
6 4
输出样例:
1
双端队列广搜(可以看做简化版的dijskral)
任意时刻双端队列中的点到目标点的距离最多分为两种(小在前,大在后)

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int N = 1005;
typedef pair<int, int> PII;
int x0, y0, t;
bool st[N][N];
int dist[N][N],g[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int bfs()
{
memset(dist, 0x3f, sizeof(dist));
deque<PII> q;
q.push_back({x0, y0});
dist[x0][y0]=0;
while(q.size())
{
auto t = q.front();
q.pop_front();
int x = t.first, y = t.second;
st[x][y]=true;
for(int i = 0; i < 4; i ++)
{
int nx = x+dx[i], ny = y+dy[i];
if(nx>=0 && nx<N && ny>=0 && ny<N)
{
if(dist[nx][ny] > dist[x][y]+g[nx][ny])
{
dist[nx][ny]=dist[x][y]+g[nx][ny];
if(g[nx][ny]) q.push_back({nx, ny});
else q.push_front({nx, ny});
}
}
}
}
return dist[0][0];
}
int main()
{
cin >> t >> x0 >> y0;
int x, y;
while(t --)
{
scanf("%d%d", &x, &y);
g[x][y] = 1;
}
cout << bfs();
return 0;
}优化一下bfs函数的细节,根据访问状态和当前位置跳过流程
int bfs()
{
memset(dist, 0x3f, sizeof(dist));
deque<PII> q;
q.push_back({x0, y0});
dist[x0][y0]=0;
while(q.size())
{
auto t = q.front();
q.pop_front();
int x = t.first, y = t.second;
if(!x && !y) break;
if(st[x][y]) continue;
st[x][y]=true;
for(int i = 0; i < 4; i ++)
{
int nx = x+dx[i], ny = y+dy[i];
if(nx>=0 && nx<N && ny>=0 && ny<N)
{
if(dist[nx][ny] > dist[x][y]+g[nx][ny])
{
dist[nx][ny]=dist[x][y]+g[nx][ny];
if(g[nx][ny]) q.push_back({nx, ny});
else q.push_front({nx, ny});
}
}
}
}
return dist[0][0];
}快了不少

1/6 AcWing 2014. 岛
每当下雨时,农夫约翰的田地总是被洪水淹没。
由于田地不是完全水平的,所以一些地方充满水后,留下了许多被水隔开的“岛”。
约翰的田地被描述为由 N 个连续高度值 H1,…,HN指定的一维场景。
假设该场景被无限高的围墙包围着,请考虑暴雨期间发生的情况:
最低处首先被水覆盖,形成一些不连贯的岛,随着水位的不断上升,这些岛最终都会被覆盖。
一旦水位等于一块田地的高度,那块田地就被认为位于水下。
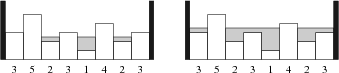
上图显示了一个示例:在左图中,我们只加入了刚好超过 1 单位的水,此时剩下 4 个岛(最大岛屿剩余数量),而在右图中,我们共加入了 7 单位的水,此时仅剩下 2 个岛。
请计算,暴风雨期间我们能在某个时间点看到的最大岛屿数量。
水会一直上升到所有田地都在水下。
输入格式
第一行包含整数 N。
接下来 N 行,每行包含一个整数表示 Hi。
输出格式
输出暴风雨期间我们能在某个时间点看到的最大岛屿数量。
数据范围
1≤N≤10^5,
1≤Hi≤10^9
贪心法

只有以上两种情况下,当中间的区域要被淹没时,总的岛屿数会变化
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
struct land {
int x, h;
bool operator < (const land& o)
{
if (h!=o.h)
return h < o.h;
else
return x < o.x;
}
} d[N];
bool is_down[N];
int n;
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i){
d[i].x = i;
scanf("%d", &d[i].h);
}
sort(d, d + n);
int cur = 1, res = 1;
for (int i = 0; i < n; ++i)
{
int x = d[i].x;
is_down[x] = 1;
bool left = x > 0 && !is_down[x - 1]; //左岛是否还在
bool right = x < n - 1 && !is_down[x + 1]; //右岛是否还在
if (left && right) cur++;
else if (!left && !right) cur--;
if (d[i + 1].h != d[i].h)
res = max(cur, res);
}
cout << res;
}
本文来自博客园,作者:泥烟,CSDN同名, 转载请注明原文链接:https://www.cnblogs.com/Knight02/p/15798995.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号