初识二分法

二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。

针对动态变化的数据集合，二分查找将不再适用。

数据量太小不适合二分查找,优势微乎其微,杀鸡用牛刀,遍历就够了

数据量太大也不适合二分查找。二分查找底层依赖数组这种数据结构的，所以太大的数据用数组存储就比较吃力,甚至内存不足以支持

例:在一个给定的有序数组[以下默认为升序]中快速寻找某个数的下标

 

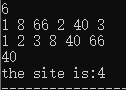
 循环实现:

#include<iostream>
#include<algorithm>
using namespace std; 
int main()
{
    int n;
    cin>>n;
    int a[n];
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    sort(a,a+n);
    for(int i=0;i<n;i++){
        cout<<a[i]<<' ';
    }
    cout<<endl;
    int value;
    cin>>value;
    int low=0,high=n-1,mid;
    int ret=1;
    while(low<=high)
    {
        mid=(low+high)/2;
        if(a[mid]==value){
            cout<<"the site is:"<<mid;
            ret=0;
            break;
        }else if(a[mid]<value){
            low=mid+1;
        }else{
            high=mid-1;
        }
    }
    if(ret){
        cout<<"no found";
    }
    return 0;
}

容易出错的 3 个地方。

1. 循环退出条件是 low<=high，而不是 low<high。

2.mid=(low+high)/2 这种写法是有问题的。因为如果 low和 high比较大的话，两者之和就有可能会溢出。改进的方法是将mid的计算方式写成low+(high-low) 2。更进一步，如果要将性能优化到极致的话，可以将这里的除以 2操作转化成位运算low+((high-low)>>1)或者(low&high)+((low^high)>>1)[注意运算符的优先级，千万不能写成这样：low+(high-low)>>1]。相比除法运算来说，计算机处理位运算要快得多。

3.low 和 high 的更新.如果直接写成 low=mid 或者 high=mid，就可能会发生死循环。

 递归实现(函数部分):

 

int search(int a[],size,value){
    return searchValue(a,0,size-1,value);
}
int searchValue(int a[],int low,int high,int value){
    if(low>high){
        return -1;
    }
    int mid = low+((high - low)>>1);
    if(a[mid]<value){
        return mid;
    }else if(a[mid]<value){
        searchValue(a,mid+1,high,value);
    }else{
        searchValue(a,low,mid-1,value);
    }
}