【选修建模的小练习】长方形椅子的稳定性探究

一.问题

椅子四条腿的椅脚连线呈长方形能在不平的地面上放稳吗？

二.问题分析

   经过分析，可以用变量表示椅子的位置，用函数表示椅子四脚与地面的距离，进而用数学语言把模型假设和椅脚同时着地表达出来.

三模型假设

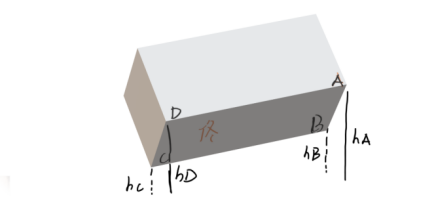
（1）椅子四条腿一样长，椅脚与地面接触处视为一点，四脚的连线呈长方形．

（2）地面高度是连续变化的，沿周围任意方向都不会出现间断 (高度突变)，即地面是连续曲面．这个假设相当于给出了椅子能放稳的必要条件．

（3）椅子在任何位置至少有三只脚同时着地．为保证这一点，要求对于椅脚的间距和椅腿的长度而言，地面是相对平坦的．因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内，如果出现深沟或凸峰(即使是连续变化的)，此时三只脚是无法同时着地的．    

四、模型建立

综上可知，解决问题的关键在于选择合适的变量，把椅子四只脚同时着地表示出来．

首先，引入合适的变量表示椅子位置的平移或旋转变换．其实平移椅子后问题的参数没有发生本质变化，所以将椅子就地旋转，找到椅子能放稳的条件．

  注意到椅脚连线呈长方形，是中心对称图形，绕它的对称中心旋转180度后，椅子仍在原地．把长方形绕它的对称中心O旋转，这可以表示椅子位置的改变。于是，旋转角度θ这一变量就表示了椅子的位置．建立直角坐标系来解决问题．

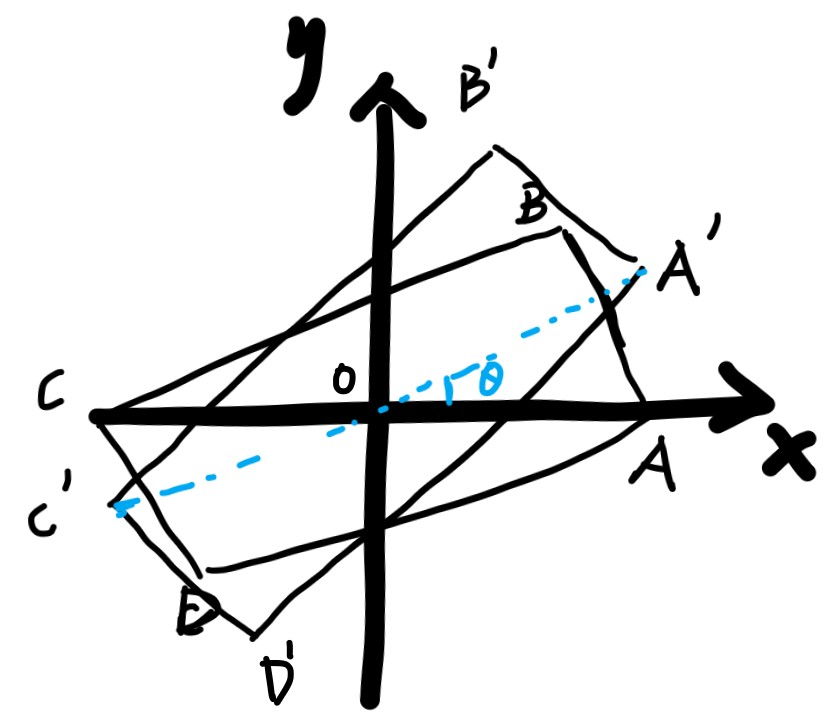
  如下图所示，设椅脚连线为长方形ABCD，以对角线AC所在的直线为x轴，对称中心O为原点，建立平面直角坐标系．椅子绕O点沿逆时针方向旋转角度θ后，长方形ABCD转至A’B’C’D’的位置，这样就可以用旋转角θ（0≤θ≤π）表示出椅子绕点O旋转θ后的位置．

  

 其次，把椅脚是否着地用数学形式表示出来．

 我们知道，当椅脚与地面的竖直距离为零时，椅脚就着地了，而当这个距离大于零时，椅脚不着地．由于椅子在不同的位置是θ的函数，因此，椅脚与地面的竖直距离也是θ的函数．

 因为椅子四只脚与地面的竖直距离有四个θ相关的函数．而由假设(3)可知，椅子在任何位置至少有三只脚同时着地，即这四个函数函数值对于任意角度θ至少有三个同时为0．因此，只需引入两个距离函数即可．考虑到长方形ABCD是中心对称图形，绕其对称中心O沿逆时针方向旋转180°后，长方形位置不变，但A,C和B,D对换了．

因此，记  A、B两脚与地面竖直距离之和为f（θ），C、D两脚与地面竖直距离之和为g（θ），其中θ∈[0，π]，从而将原问题数学化。

数学模型：已知f（θ）和g（θ）是θ的非负连续函数，对∀θ，f（θ）•g(θ)＝0，证明：∃θ0∈[0，π]，使得f（θ0）＝g（θ0）＝0成立。   

 

 

五、模型求解  

①若f（0）＝g（0）＝0，那么结论成立。

②若f（0）与g（0）不同时为零，不妨设f（0）＞0，g（0）＝0。将长方形ABCD绕点O逆时针旋转角度π后，A，B与C，D互换，但长方形ABCD在地面上所处的位置不变，由此可知，f（π）＝g（0），g（π）＝f（0）.∴f（0）＞0，g（0）＝0 → g（π）＞0，f（π）＝0。

令h（θ）＝f(θ)－g（θ），由f(θ)和g(θ)的连续性知h(θ)也是连续函数。

又h（0）＝f(0)－g（0）＞0，h（π）＝f(π)－g（π）＜0，

根据连续函数介值定理，必存在θ0∈（0，π）使得h（θ0）＝0，即f（θ0）＝g（θ0） ；

又因为f（θ0）•g（θ0）＝0，

所以f（θ0）＝g（θ0）＝0。即四只脚同时着地，稳定。