概率论与数理统计笔记
第一章: 概率论的基本概念
古典概型



\(P(A) = \frac{30!}{365^{30}}\)
\(P(B) = 1-\frac{C_{365}^{30}30!}{365^{30}}\)
\(P(C) = \frac{C_{30}^{3}3! {362}^{27}}{{365}^{30}}\)


\(P(1) = \frac{C_{20}^{15}40^{15}60^5}{100^{20}}\)
\(P(2) = \frac{C_{40}^{15}C_{60}^{5}}{C_{100}^{20}}\)
\(P(3) = \frac{40}{100}\)
\(P(4) = \frac{C_{40}^{1}A_{99}^{19}}{A_{100}^{20}} = \frac{40}{100}\)
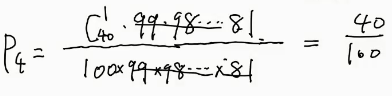
几何概型


概率为零,不一定是不可能事件
公式求概率

1.②③对偶律
独立

相互独立 两两独立


- 必然事件与任何事件都相互独立
- 不可能事件φ与任何事件都相互独立
条件概率
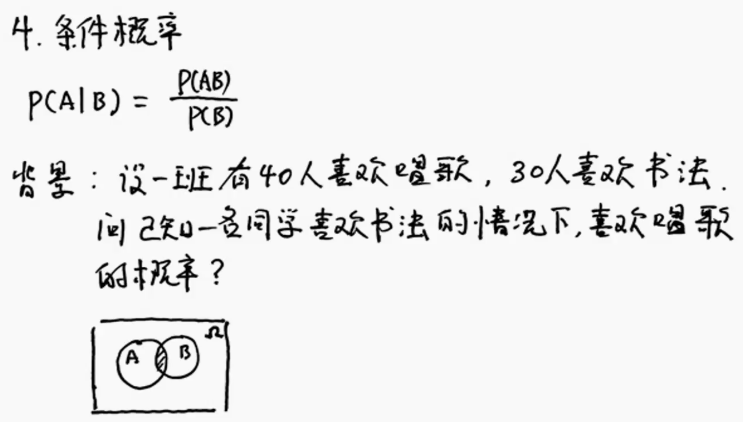
乘法公式
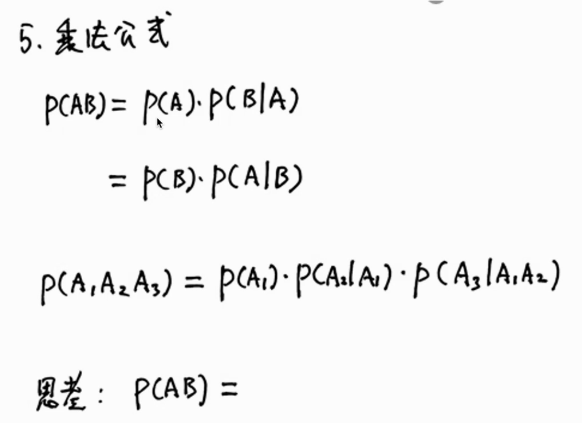
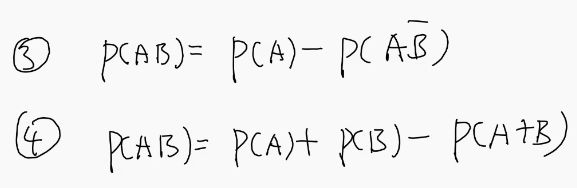

🔥A

🔥B,C,D

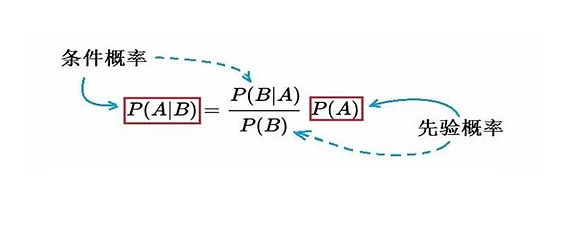
贝叶斯公式与全概率公式 (💡注意是否为"完备事件组")

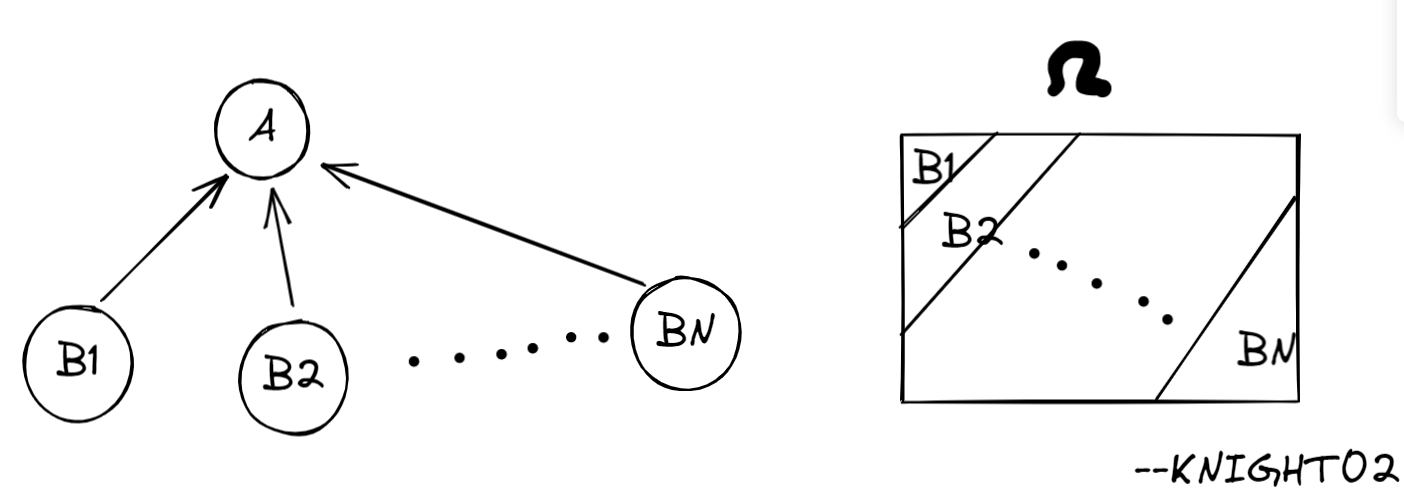




(1)中甲乙互斥,B1,B2是完备事件组
※(2)中B1,B2不是完备事件组
1️⃣\(A=\{命中\} B_{1}=\{甲射击\} B_{2}=\{乙射击\}\)
\(P(B_{1}|A) = \frac{P(AB_{1})}{P(A)} = \frac{P(B_1)P(A|B_{1})}{P(A)} = \frac{\frac{1}{2}*0.6}{\frac{1}{2}*0.6+\frac{1}{2}*0.5} = \frac{6}{11}\)
2️⃣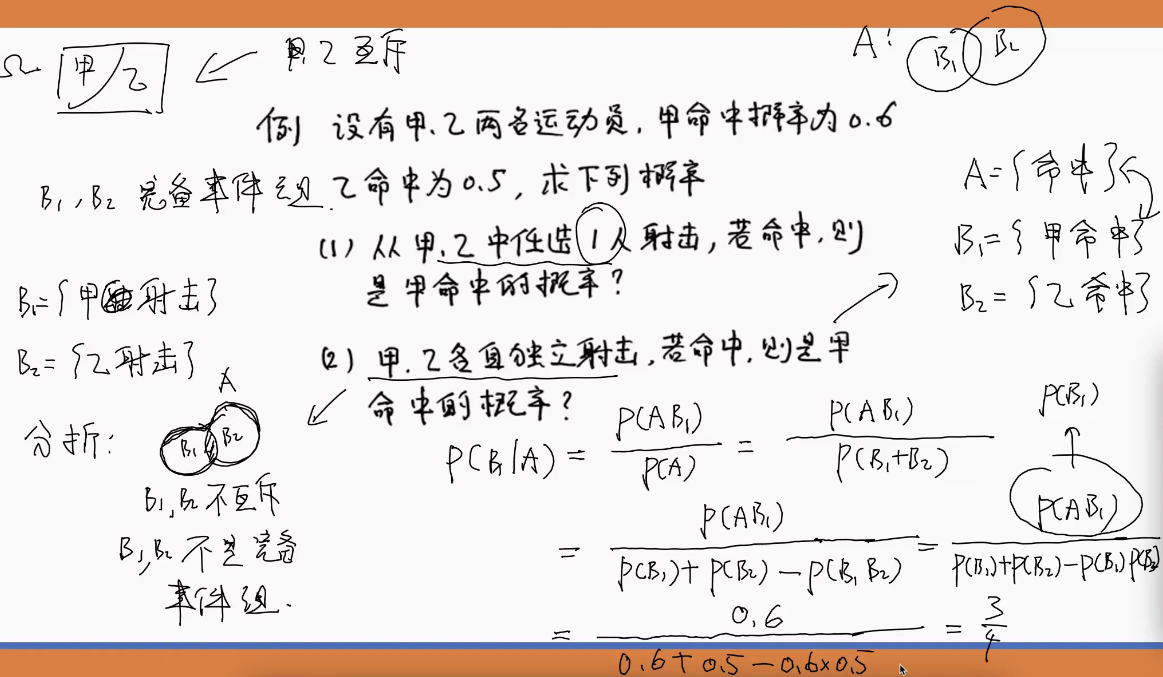

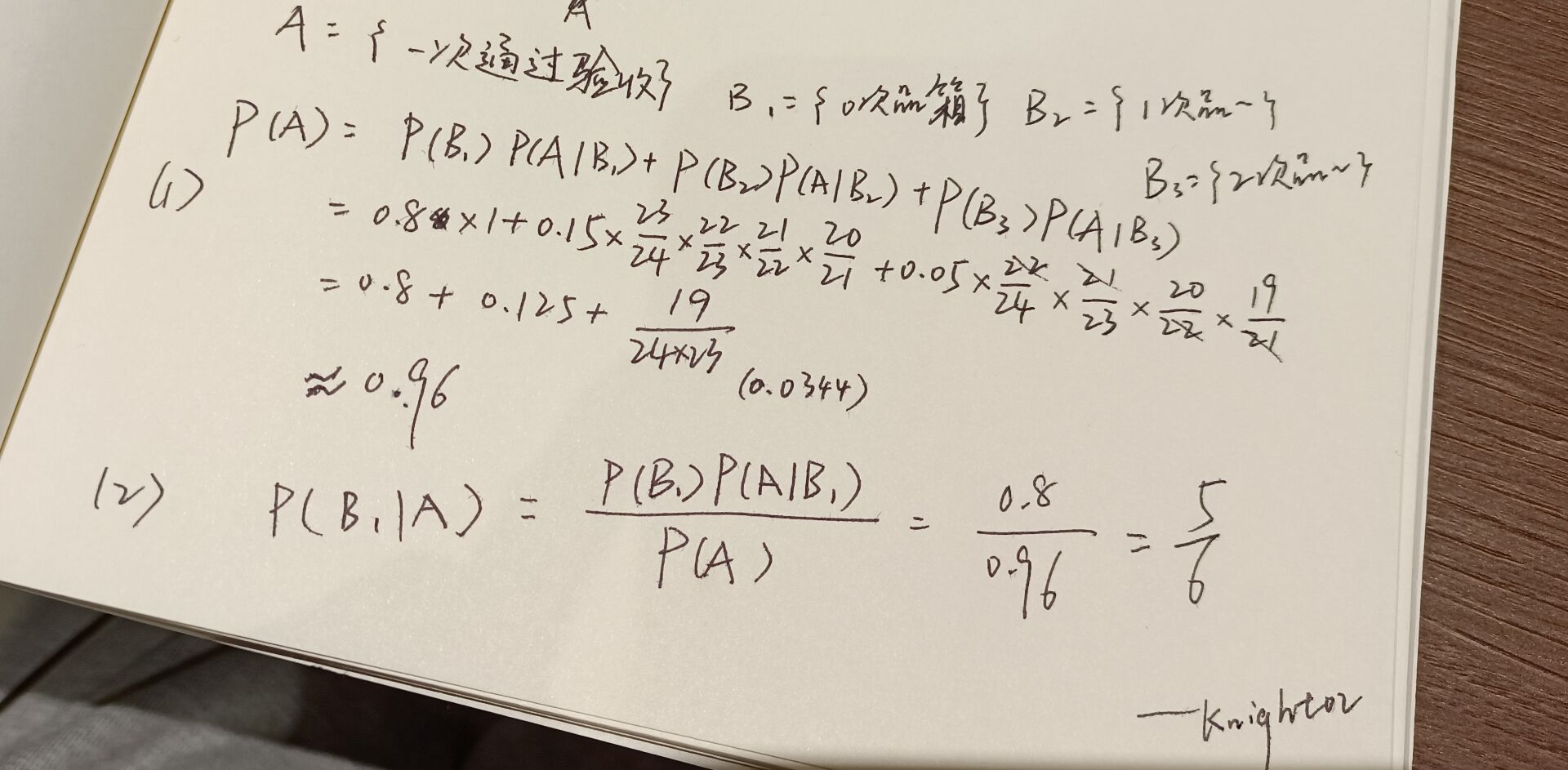

最值公式
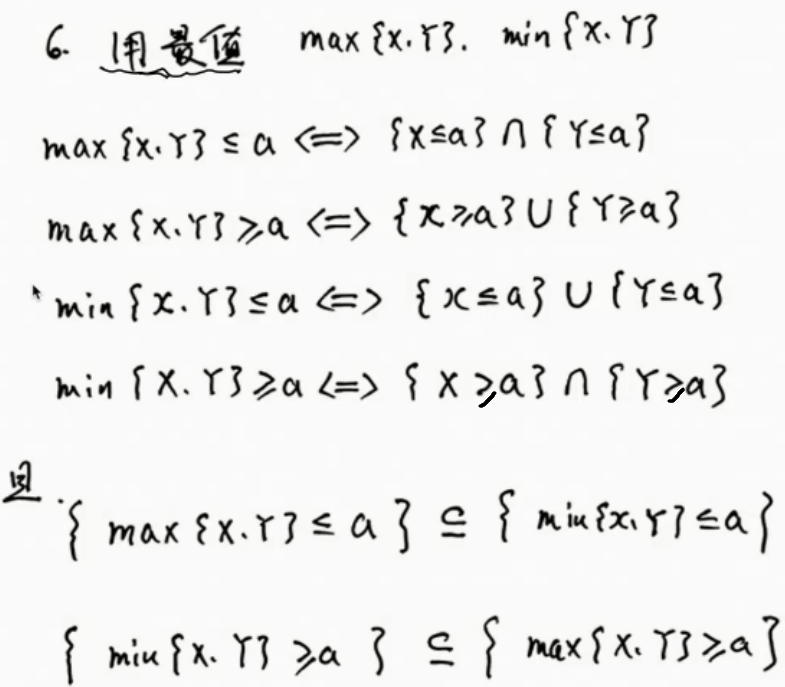

第二章: 一维随机变量及其分布
随机变量与分布函数
分布函数




典型问题: 判分布,求分布

例题




8个分布(1~5离散, 6~8连续)
1.0-1分布

2.二项分布


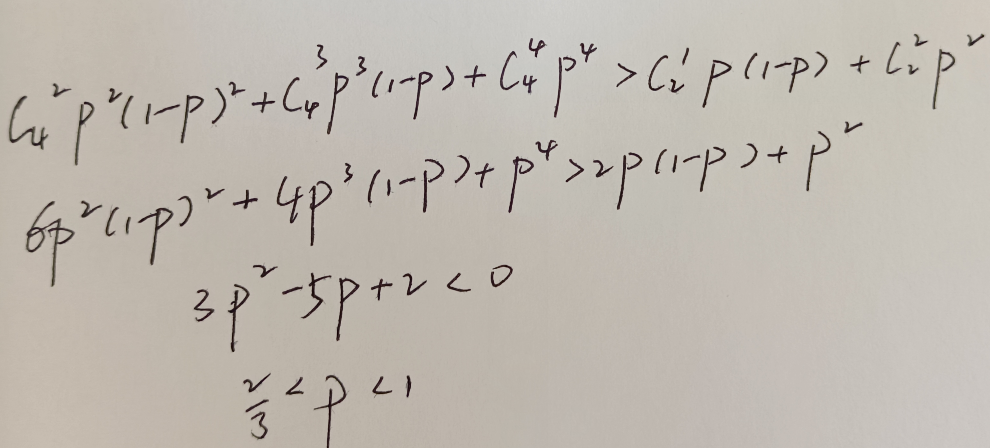
3.几何分布

4.超几何分布

5.泊松分布


6.均匀分布

7.指数分布

有的教材写作:
\(f(x) =
\left\{\begin{matrix}
λe^{-λx} ,x>=0\\
0 , x<0
\end{matrix}\right.
\)
更能反映与泊松分布的关系

性质
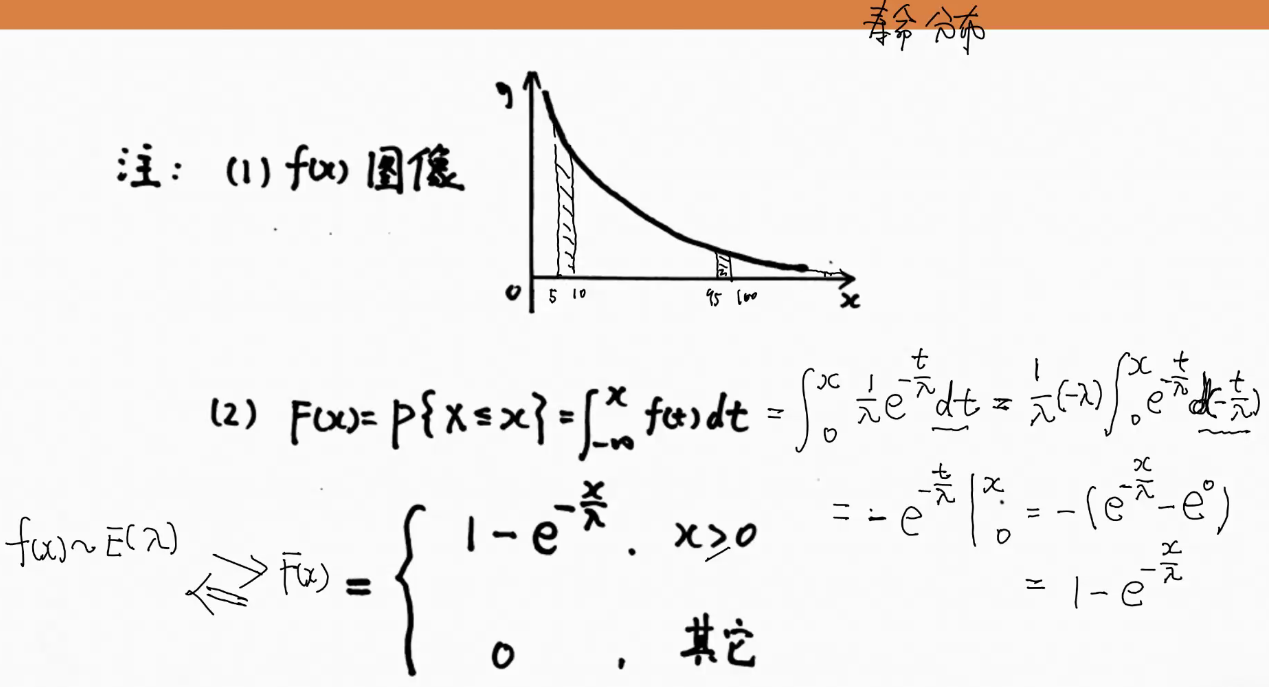

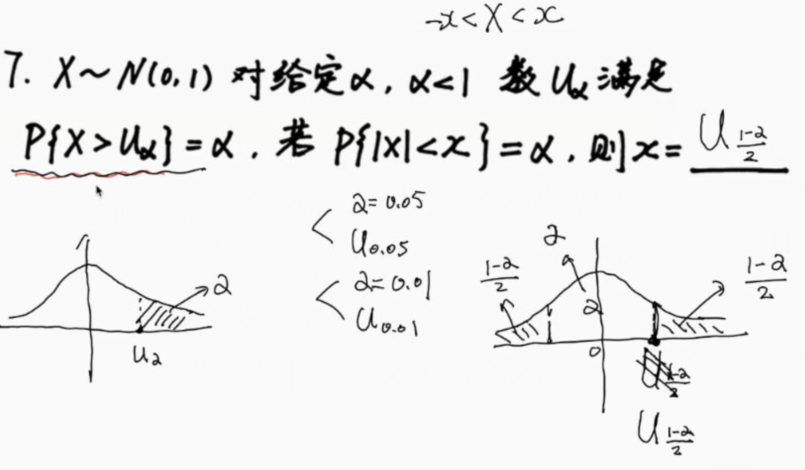
8.正态分布
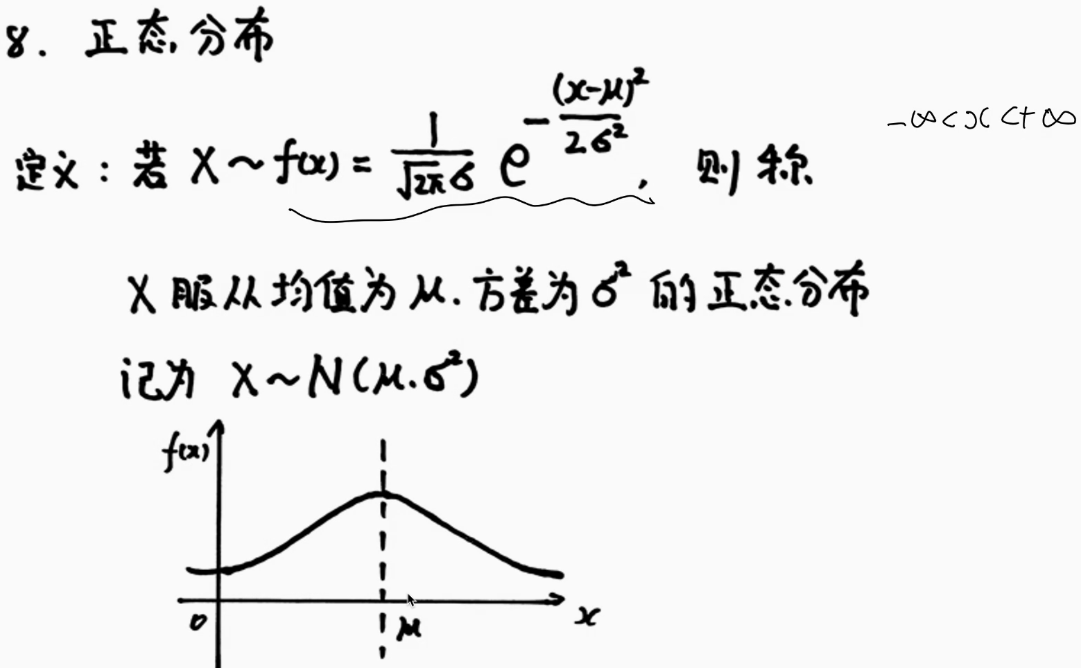
密度函数特殊 | 标准化
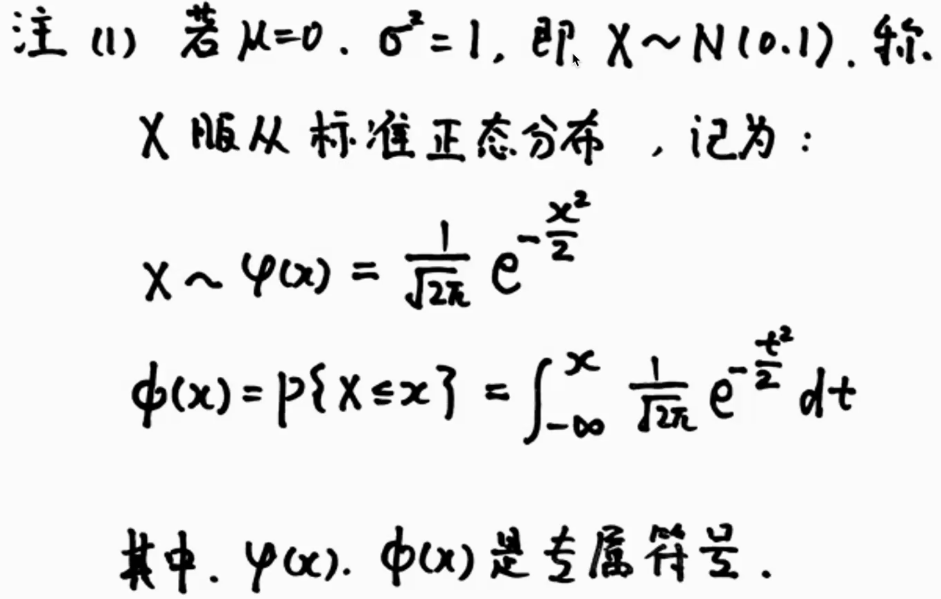

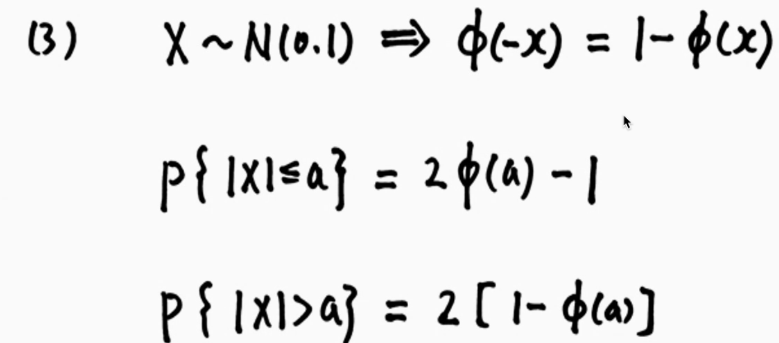
常见变形

例题
首先: F() = 1求未知数
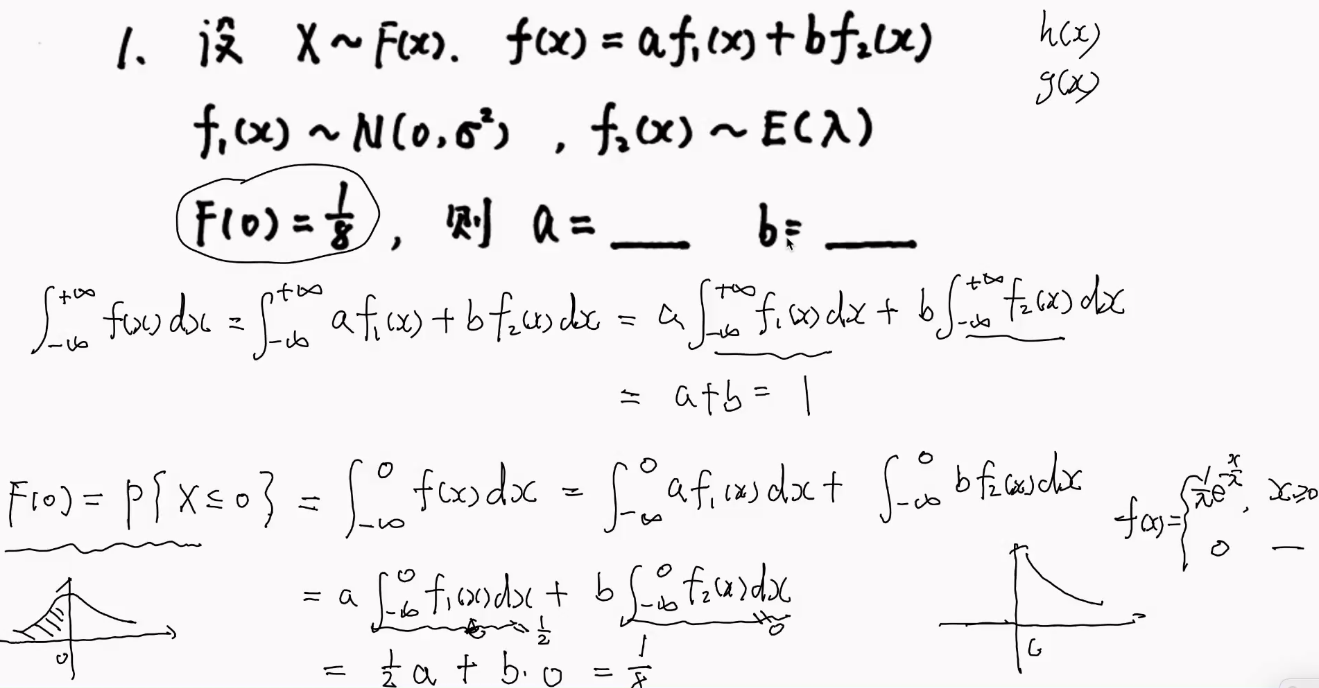
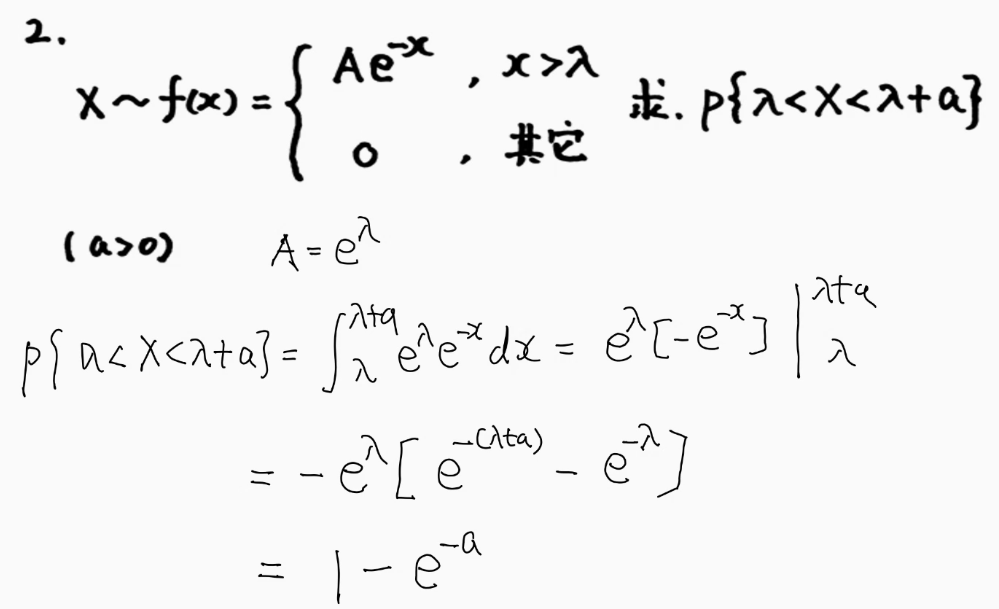
复合型
(外二项分布,内指数分布)



(外二项分布,内均匀分布)
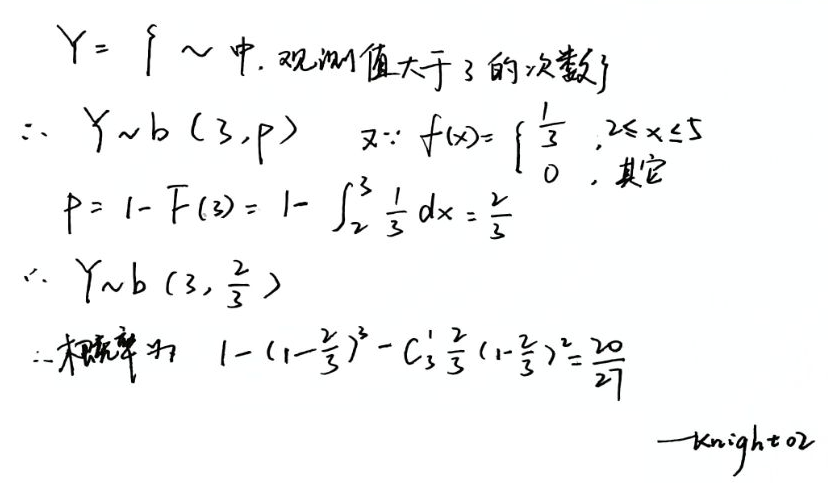


独立事件--贝叶斯---(二项分布求未知变量)--💡

求函数分布


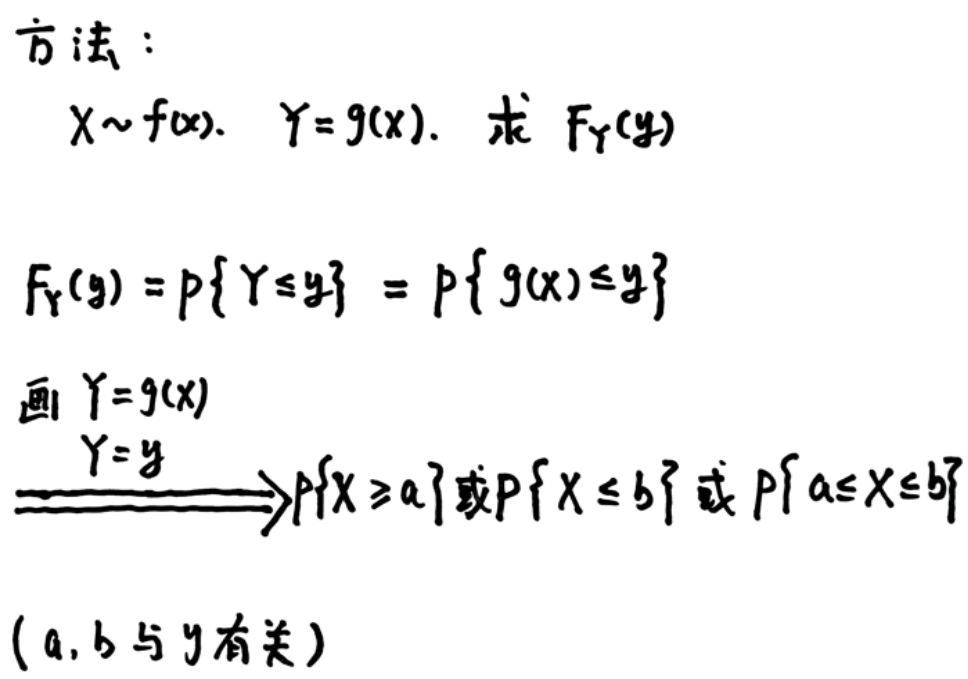

一定在正概率密度区域上画
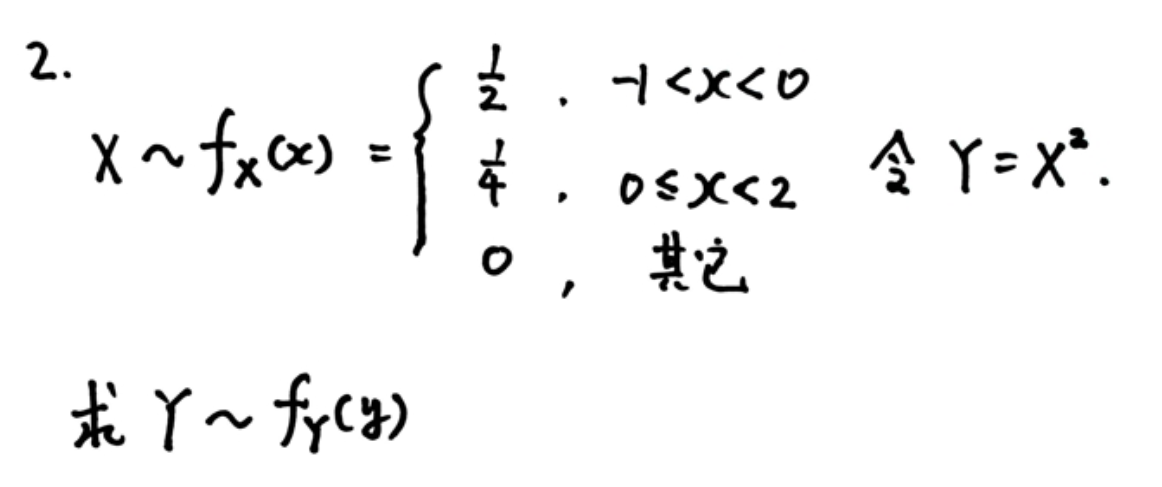

第三章: 多维随机变量

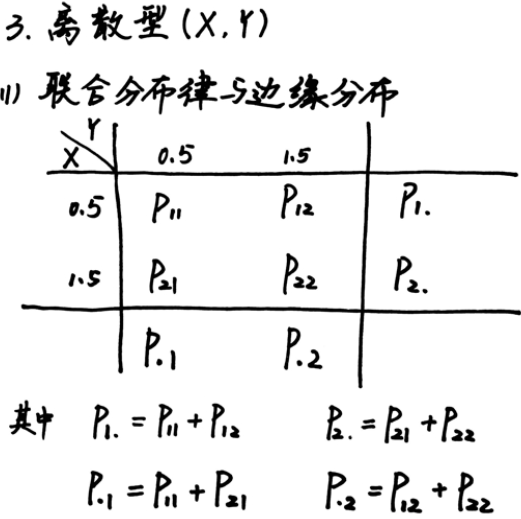
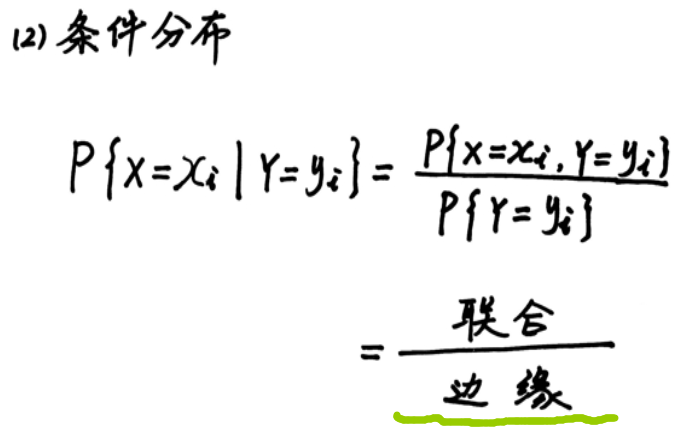
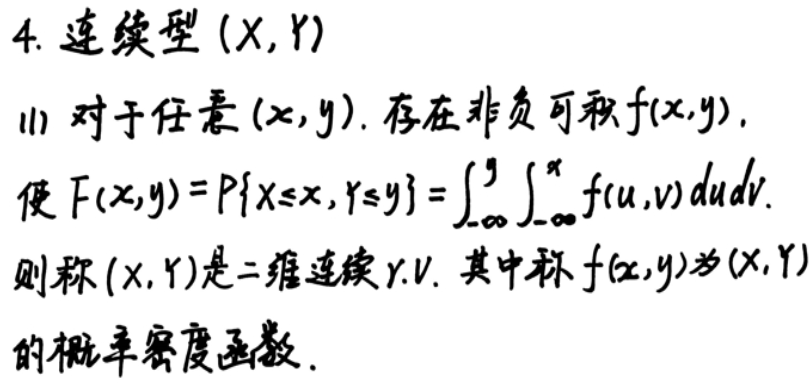
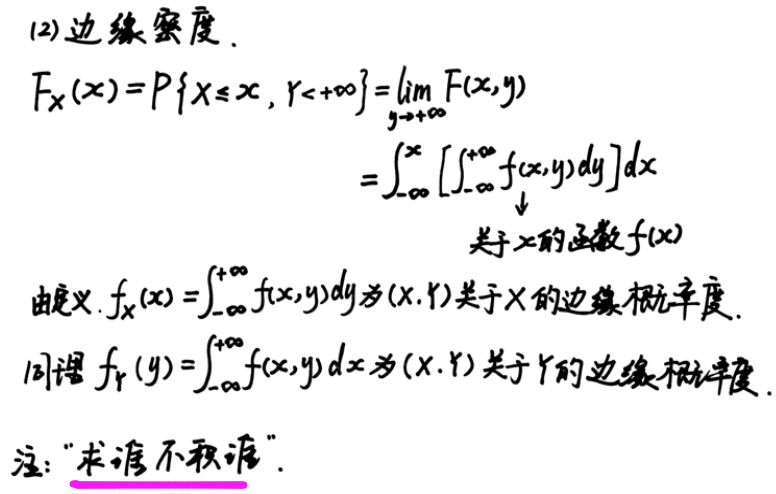
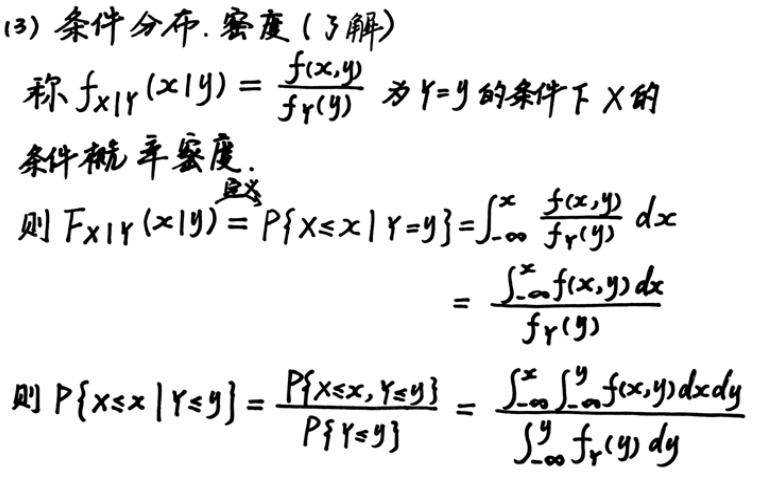
独立性
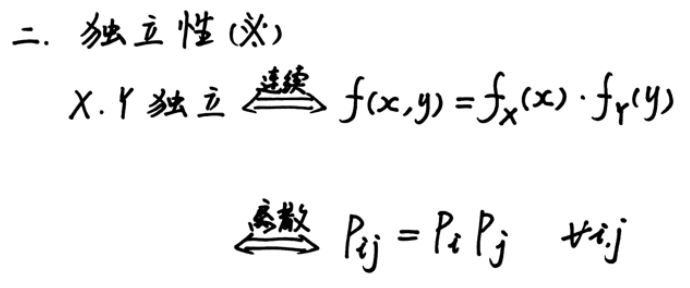
例题
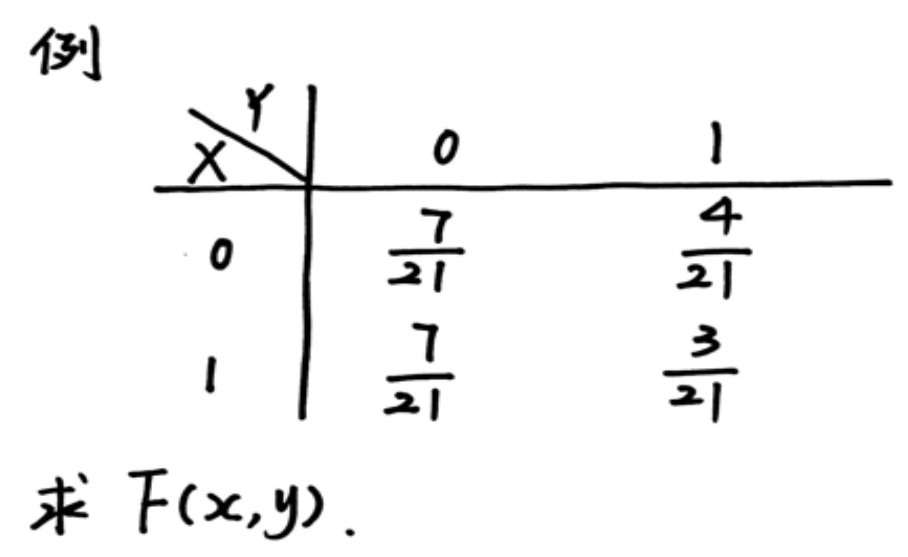

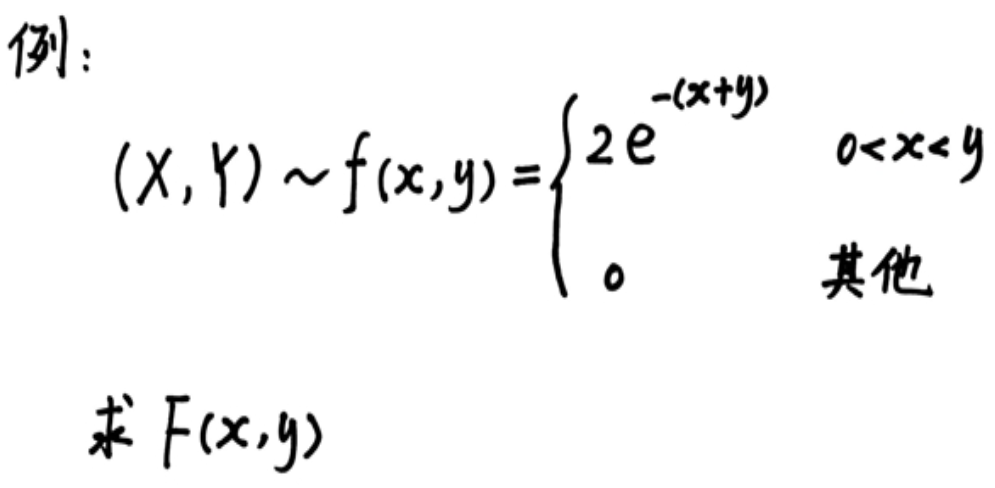
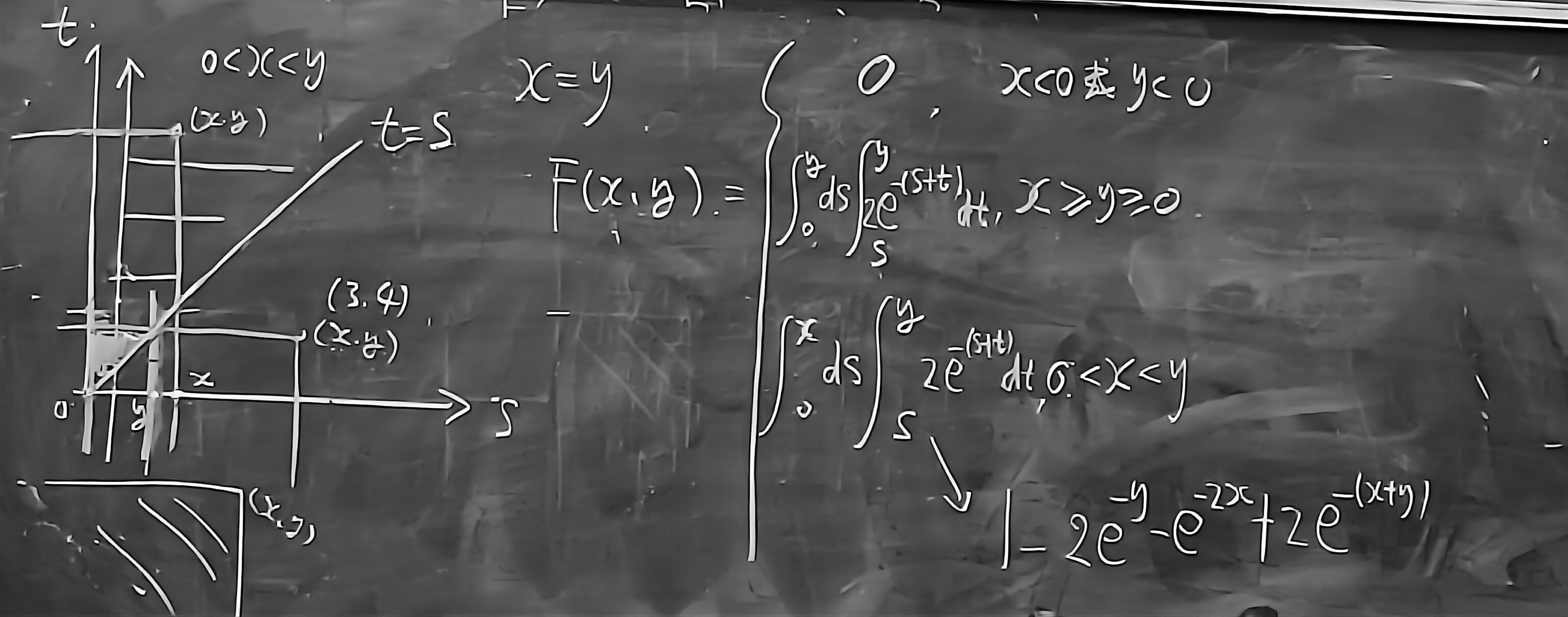



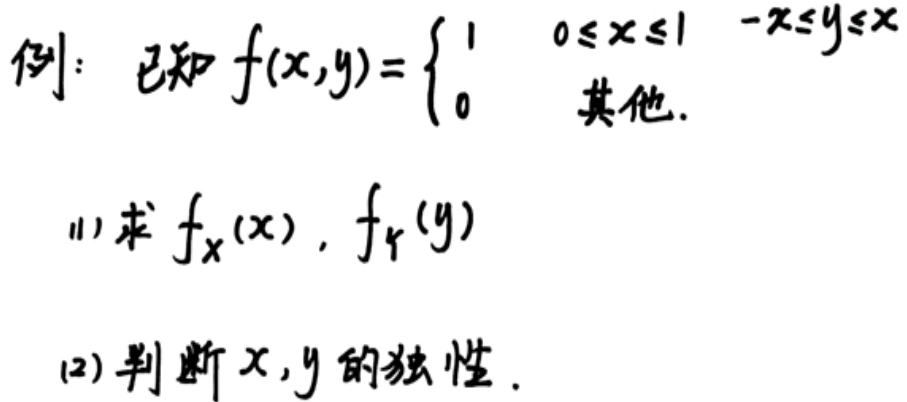

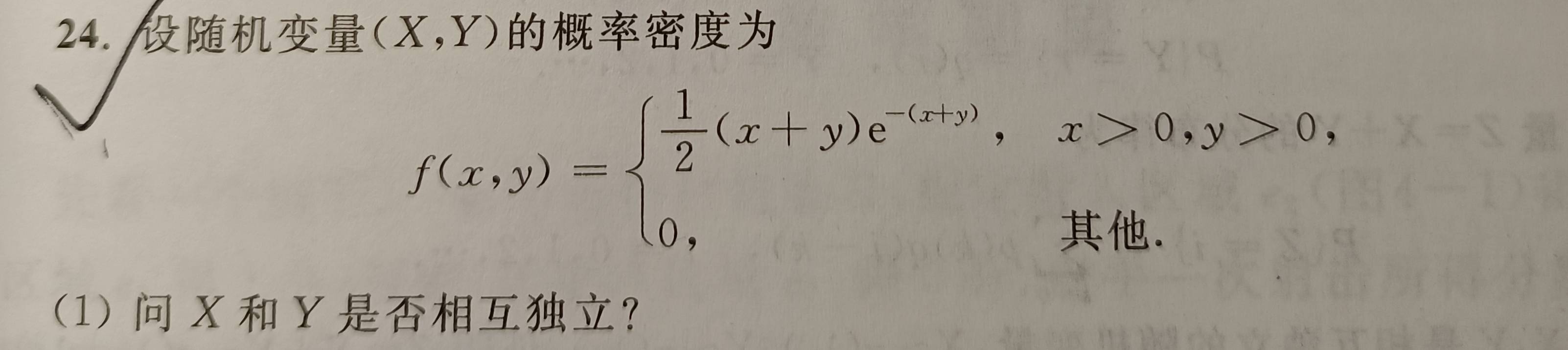

卷积公式
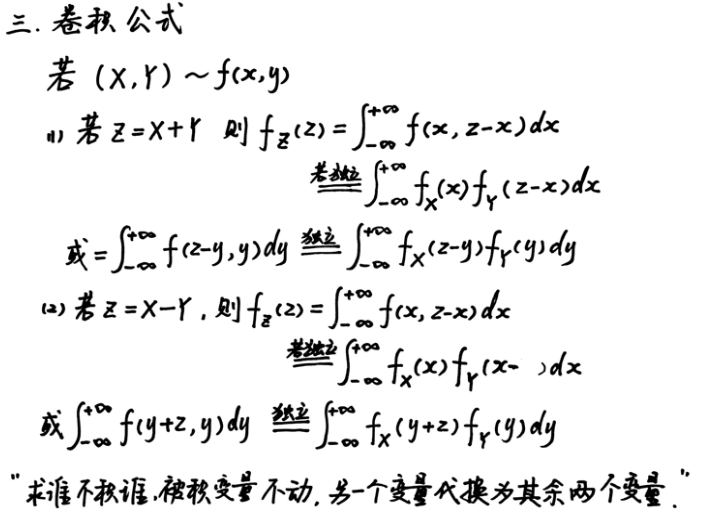

数字特征
期望

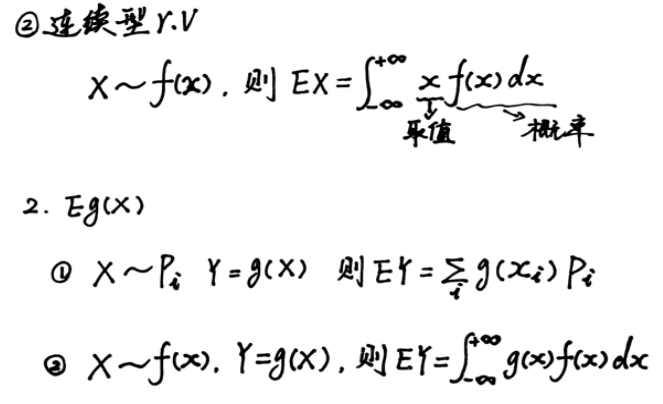
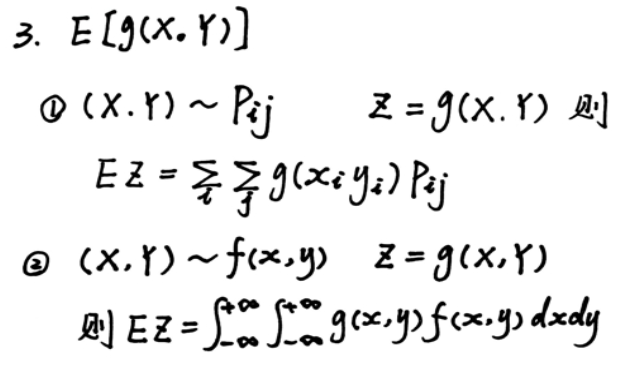
方差
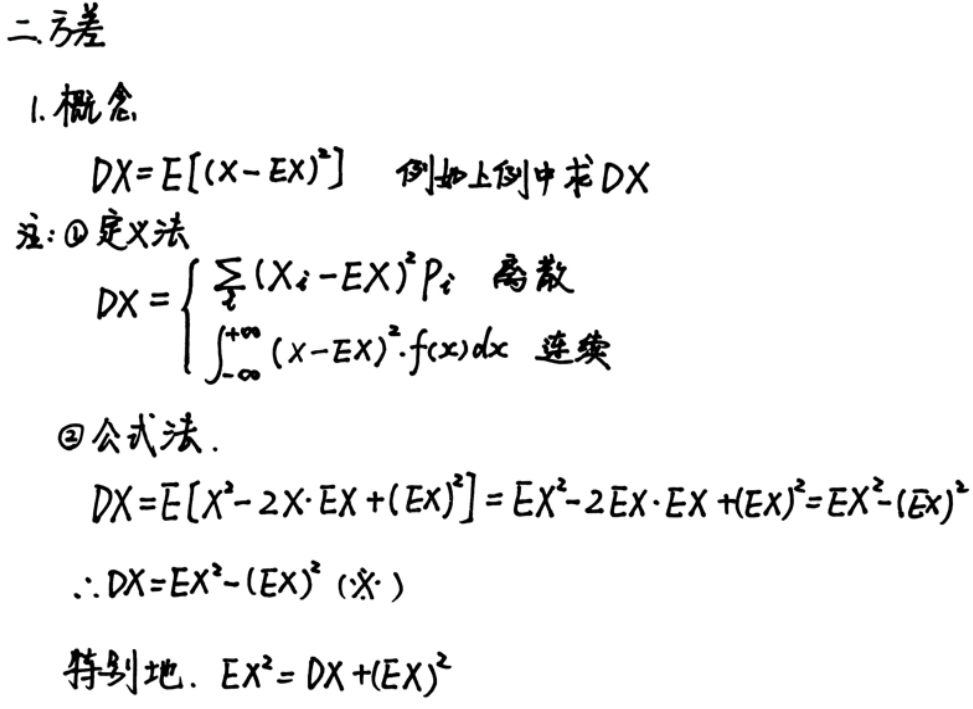
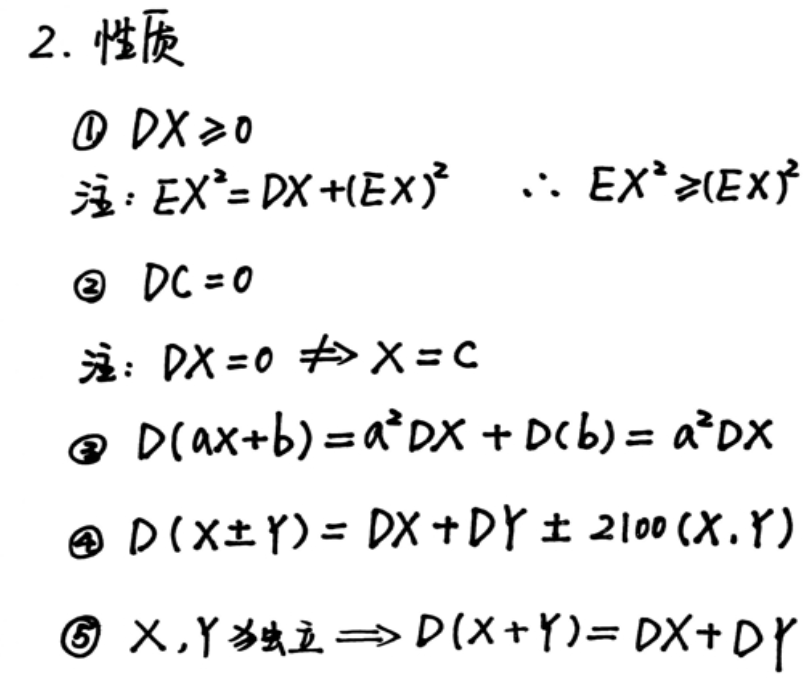
常用EX, DX
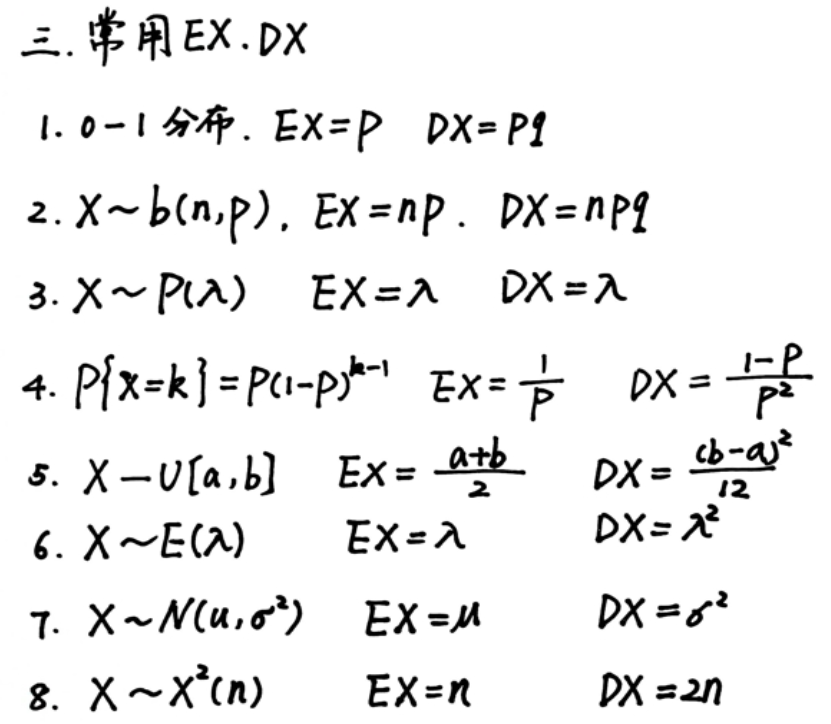
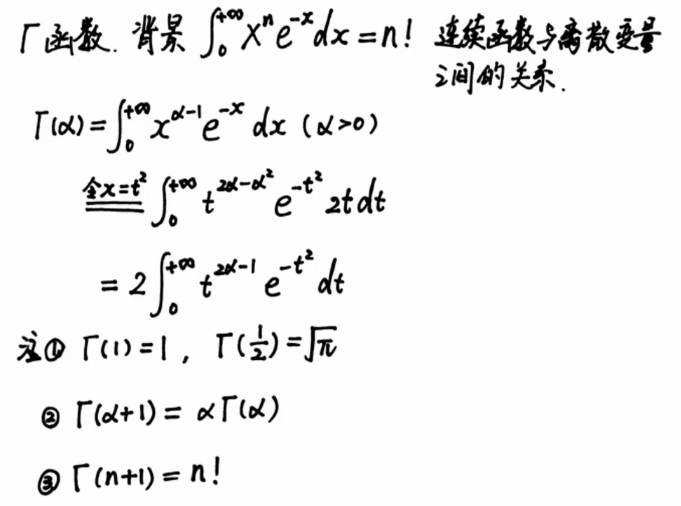

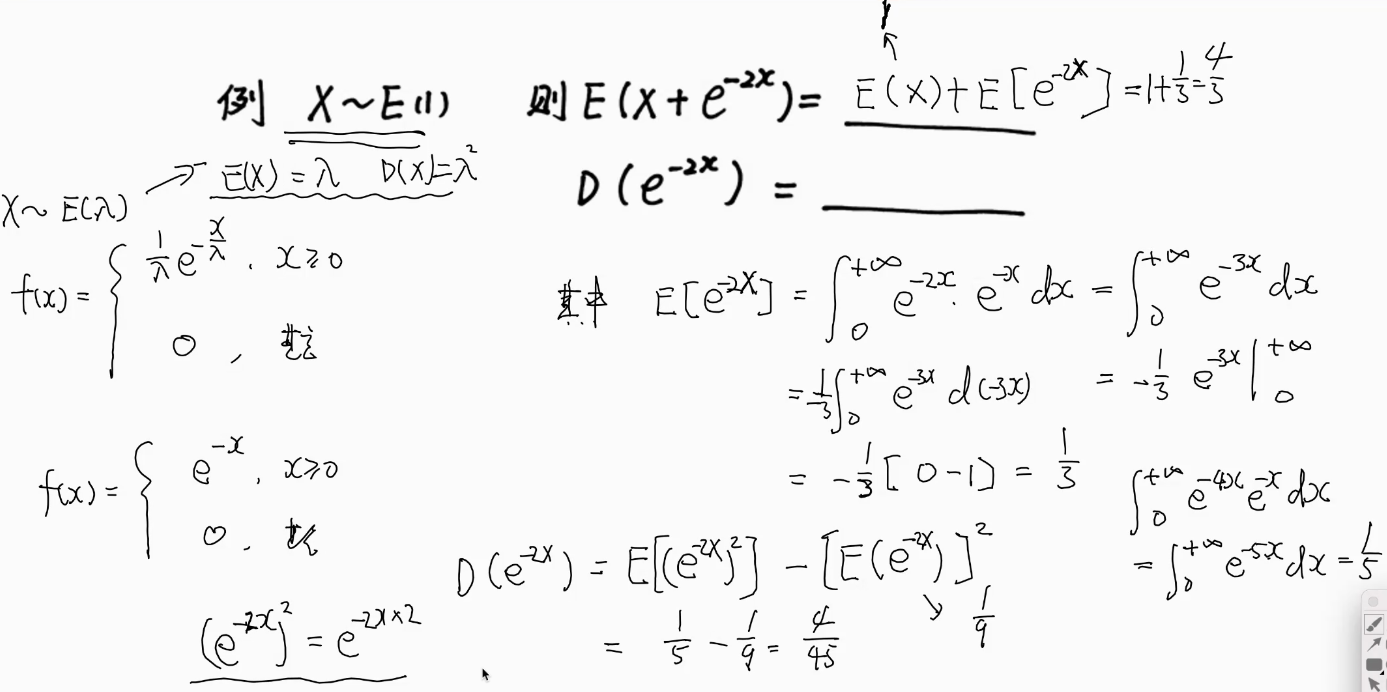
协方差
协方差等于零 <=> 无线性关系
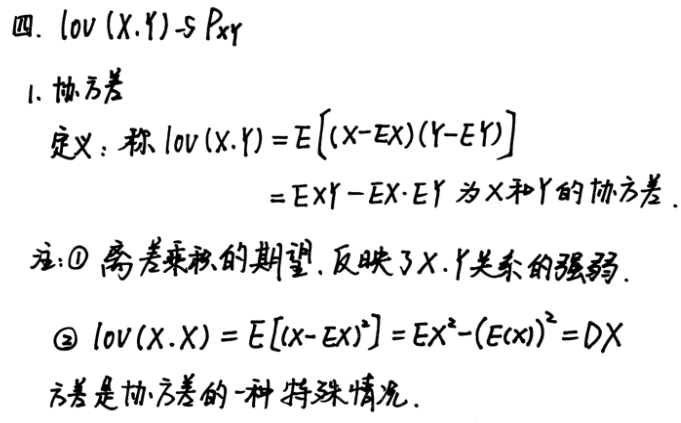




独立性与相关性
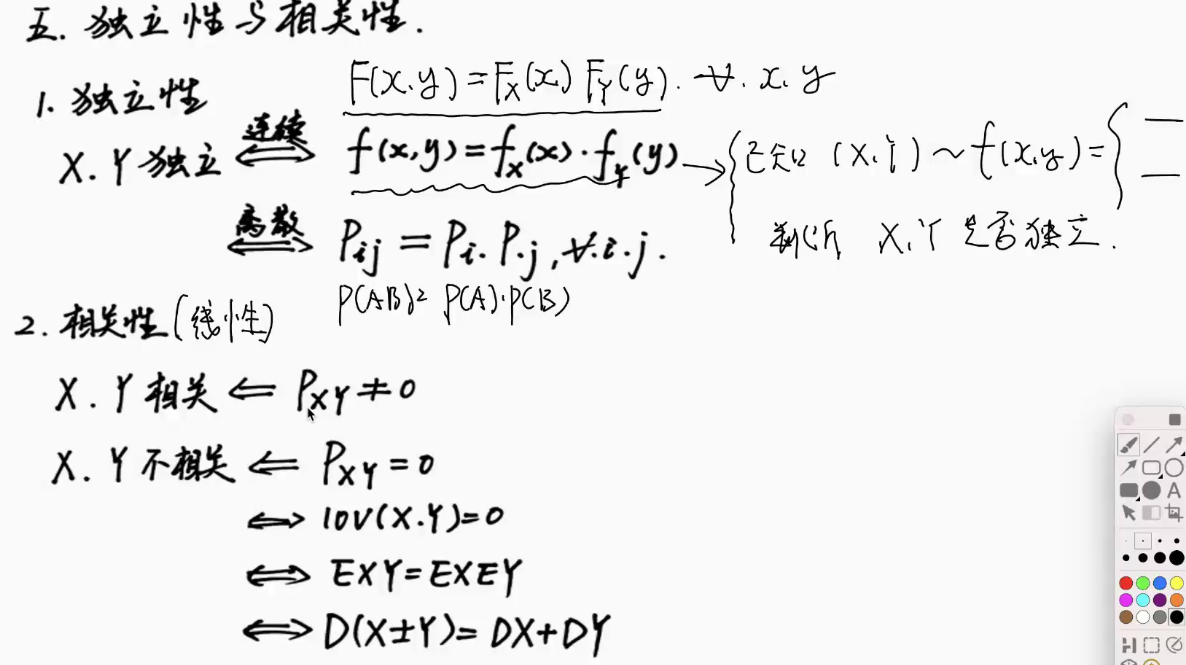
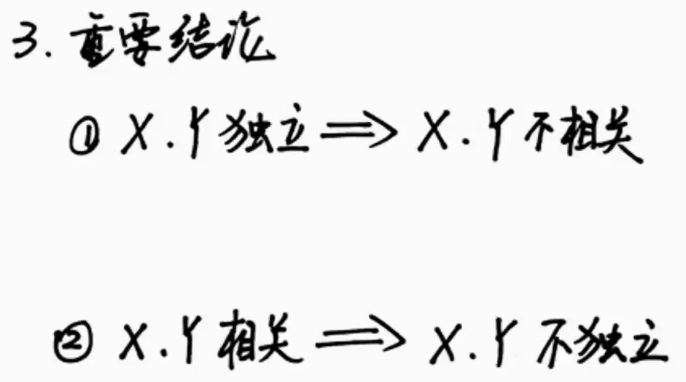


切比雪夫不等式
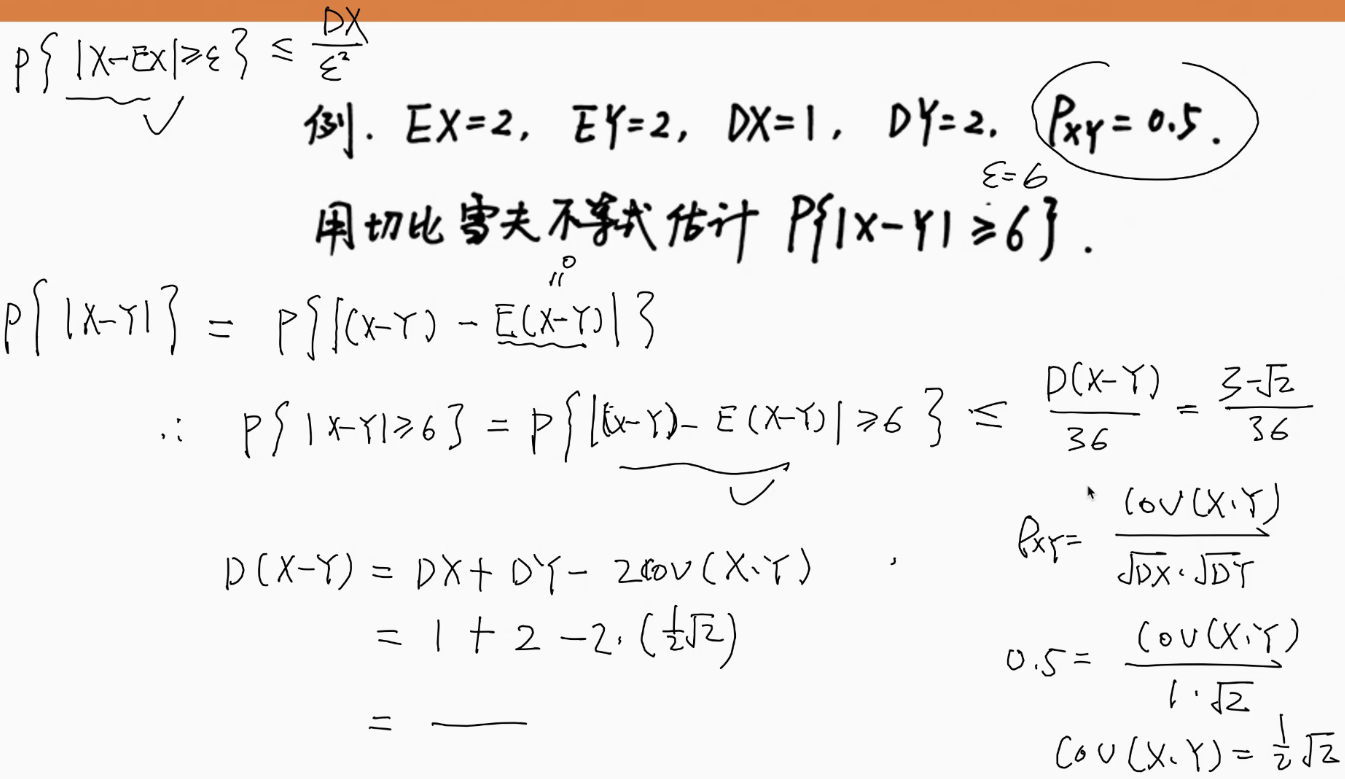
6
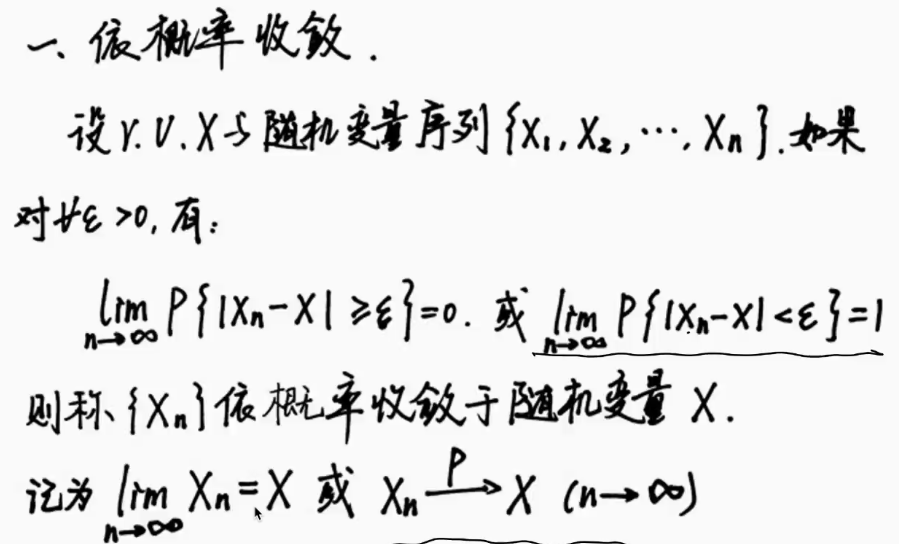




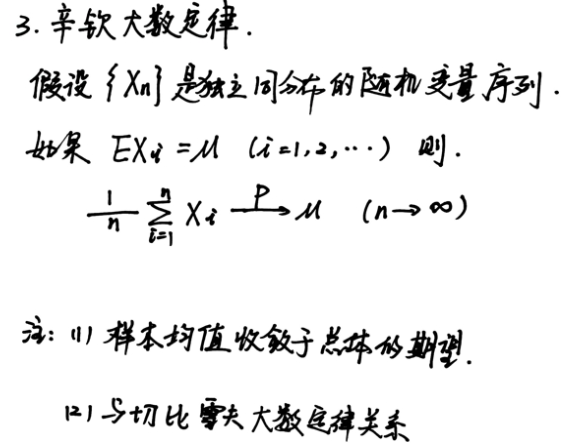




本文来自博客园,作者:泥烟,CSDN同名, 转载请注明原文链接:https://www.cnblogs.com/Knight02/articles/probability.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号