多元线性回归的梯度下降

目录

• 预测(带入)
• 代价函数
• 多变量梯度下降
  • 计算梯度
  • 梯度下降

通过房子的大小,卧室数量,层数,房龄预测价格

Size (sqft)	Number of Bedrooms	Number of floors	Age of Home	Price (1000s dollars)
2104	5	1	45	460
1416	3	2	40	232
852	2	1	35	178

预测(带入)

"""
single predict using linear regression
Args:
  x (ndarray): Shape (n,) example with multiple features
  w (ndarray): Shape (n,) model parameters   
  b (scalar):             model parameter 
  
Returns:
  p (scalar):  prediction
"""
def predict(x, w, b): 
    p = np.dot(x, w) + b     
    return p    

代价函数

\[J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 \]

\[f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b \]

"""
compute cost
Args:
  X (ndarray (m,n)): Data, m examples with n features
  y (ndarray (m,)) : target values
  w (ndarray (n,)) : model parameters  
  b (scalar)       : model parameter

Returns:
  cost (scalar): cost
"""

def compute_cost(X, y, w, b):
    m = X.shape[0]
    cost = 0.0
    for i in range(m):
        f_wb_i = np.dot(X[i], w) + b
        cost += (f_wb_i - y[i])**2
    cost /= 2*m
    return cost


X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([460, 232, 178])
b_init = 785.1811367994083
w_init = np.array([ 0.39133535, 18.75376741, -53.36032453, -26.42131618])

cost = compute_cost(X_train, y_train, w_init, b_init)
print(f'Cost at optimal w : {cost}')

Cost at optimal w : 1.5578904330213735e-12

多变量梯度下降

重复, 直到收敛

\[\begin{align*} \text{loop}&\text{ until convergence:} \; \lbrace \newline\; & w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \; & \text{for j = 0..n-1}\newline &b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*}\]

n: 特征数量, m: 训练集的个数

\[\begin{align} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \end{align} \]

计算梯度

"""
Computes the gradient for linear regression 
Args:
  X (ndarray (m,n)): Data, m examples with n features
  y (ndarray (m,)) : target values
  w (ndarray (n,)) : model parameters  
  b (scalar)       : model parameter

Returns:
  dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. 
  dj_db (scalar):       The gradient of the cost w.r.t. the parameter b. 
"""
def compute_gradient(X, y, w, b):
    m, n = X.shape          #(m:number of examples, n:number of features)
    dj_dw = np.zeros((n,))
    dj_db = 0.
    
    for i in range(m):
        dif = np.dot(X[i], w) + b - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j] + dif * X[i, j]
        dj_db = dj_db + dif
    dj_dw /= m
    dj_db /= m
        
    return dj_db, dj_dw
			
			
tmp_dj_db, tmp_dj_dw = compute_gradient(X_train, y_train, w_init, b_init)
print(f'dj_db at initial w,b: {tmp_dj_db}')
print(f'dj_dw at initial w,b: \n {tmp_dj_dw}')

dj_db at initial w,b: -1.6739251122999121e-06
dj_dw at initial w,b:
[-2.73e-03 -6.27e-06 -2.22e-06 -6.92e-05]

梯度下降

"""
Performs batch gradient descent to learn theta. Updates theta by taking 
num_iters gradient steps with learning rate alpha

Args:
  X (ndarray (m,n))   : Data, m examples with n features
  y (ndarray (m,))    : target values
  w_in (ndarray (n,)) : initial model parameters  
  b_in (scalar)       : initial model parameter
  cost_function       : function to compute cost
  gradient_function   : function to compute the gradient
  alpha (float)       : Learning rate
  num_iters (int)     : number of iterations to run gradient descent
  
Returns:
  w (ndarray (n,)) : Updated values of parameters 
  b (scalar)       : Updated value of parameter 
"""
def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): 
    
    # An array to store cost J and w's at each iteration primarily for graphing later
    J_history = []
    w = copy.deepcopy(w_in)  #avoid modifying global w within function
    b = b_in
    
    for i in range(num_iters):

        # Calculate the gradient and update the parameters
        dj_db,dj_dw = gradient_function(X, y, w, b)

        # Update Parameters using w, b, alpha and gradient
        w = w - alpha * dj_dw
        b = b - alpha * dj_db
      
        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(X, y, w, b))

        # Print cost every at intervals 10 times or as many iterations if < 10
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f}   ")
        
    return w, b, J_history

测试

# initialize parameters
initial_w = np.zeros_like(w_init)
initial_b = 0.
# some gradient descent settings
iterations = 1000
alpha = 5.0e-7
# run gradient descent 
w_final, b_final, J_hist = gradient_descent(X_train, y_train, initial_w, initial_b,
                                                    compute_cost, compute_gradient, 
                                                    alpha, iterations)
print(f"b,w found by gradient descent: {b_final:0.2f},{w_final} ")
m,_ = X_train.shape
for i in range(m):
    print(f"prediction: {np.dot(X_train[i], w_final) + b_final:0.2f}, target value: {y_train[i]}")

Iteration 0: Cost 2529.46
Iteration 100: Cost 695.99
Iteration 200: Cost 694.92
Iteration 300: Cost 693.86
Iteration 400: Cost 692.81
Iteration 500: Cost 691.77
Iteration 600: Cost 690.73
Iteration 700: Cost 689.71
Iteration 800: Cost 688.70
Iteration 900: Cost 687.69
b,w found by gradient descent: -0.00,[ 0.2 0. -0.01 -0.07]
prediction: 426.19, target value: 460
prediction: 286.17, target value: 232
prediction: 171.47, target value: 178

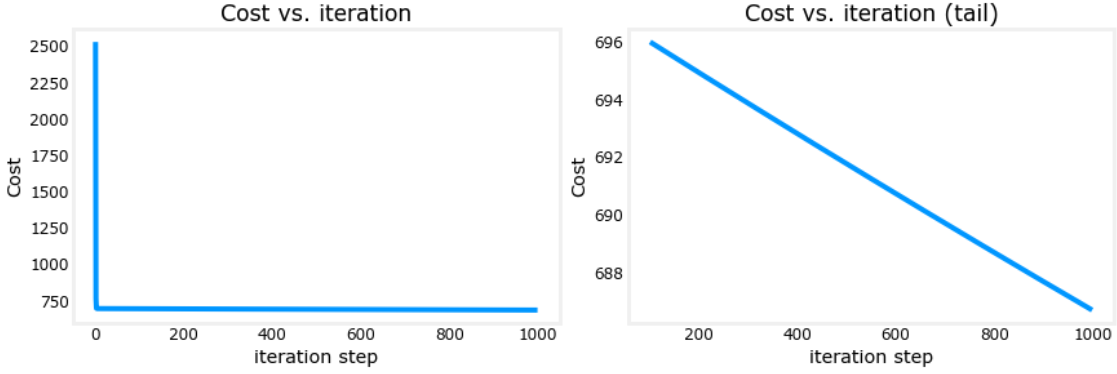
绘制cost-iteration图像

# plot cost versus iteration  
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
ax1.plot(J_hist)
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])
ax1.set_title("Cost vs. iteration");  ax2.set_title("Cost vs. iteration (tail)")
ax1.set_ylabel('Cost')             ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')   ;  ax2.set_xlabel('iteration step') 
plt.show()