[Games101笔记]Lecture1-2

该笔记基于闫令琪大神的cs课程及课后作业总结而成

---

学习过程中遇到的一些词

• Geometrically: Parallelogram law & Triangle law
  几何：平行四边形定律和三角形定律

• Algebraically: Simply add coordinates
  代数上：简单地添加坐标

• usually orthogonal unit
  通常正交单元

• Cartesian Coordinates
  笛卡尔坐标

• Dot product
  点积

• Cross product
  交叉积

• Orthonormal bases and coordinate frames
  正交基与坐标框架

• Decompose a vector
  分解向量

• dual matrix of vector a
  向量a的对偶矩阵

• homogenous coordinate
  齐次坐标

线代基础

点乘可分解向量以及判断向量之间接近or远离

叉乘可判断方位

点乘

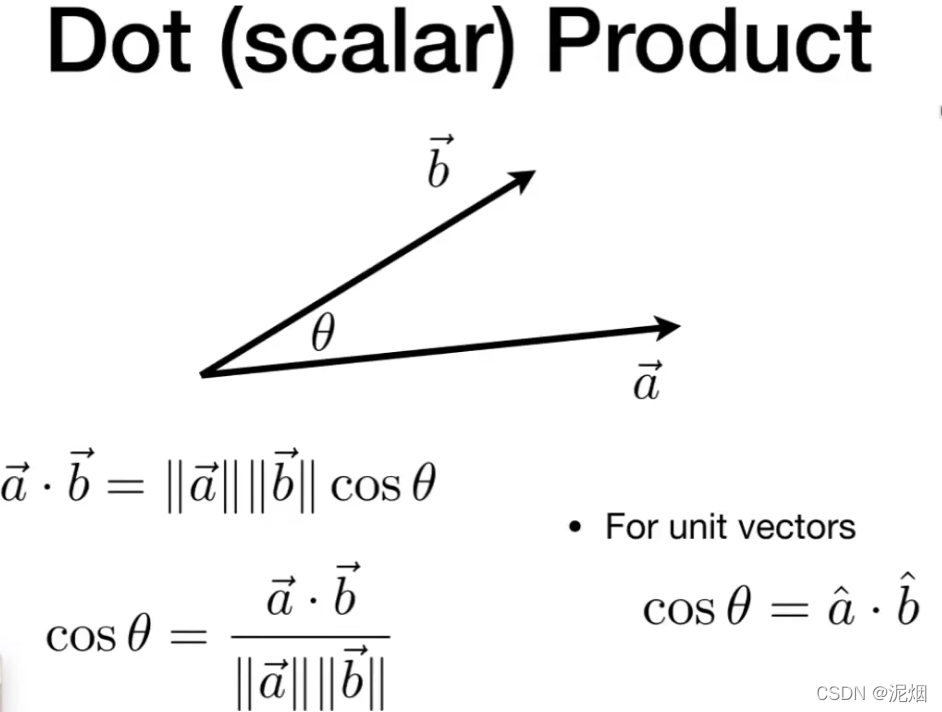
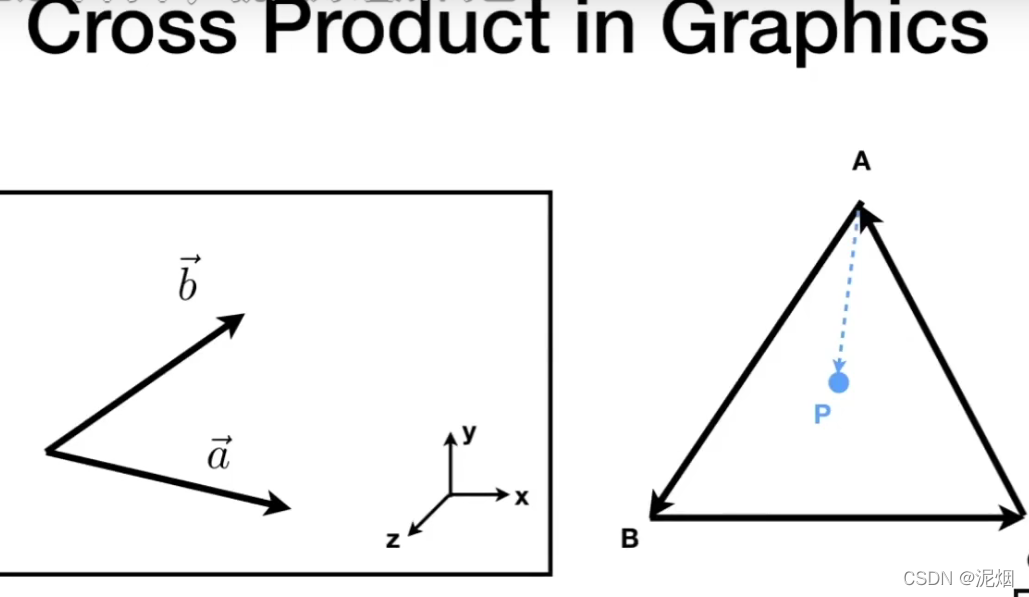
叉乘求得的结果垂直于两个原始向量，因此常用于求法线, 所以三维软件会提供翻转法线的功能 opengl永远是右手系，DirectX经常是左手系

a在b的左侧的意思是，a经过不大于180°的逆时针旋转可以与b的方向一致，右侧同理，方向变为顺时针

点在所有向量左侧或在所有向量左侧，就是多边形内部

Eigen库的用处

Eigen

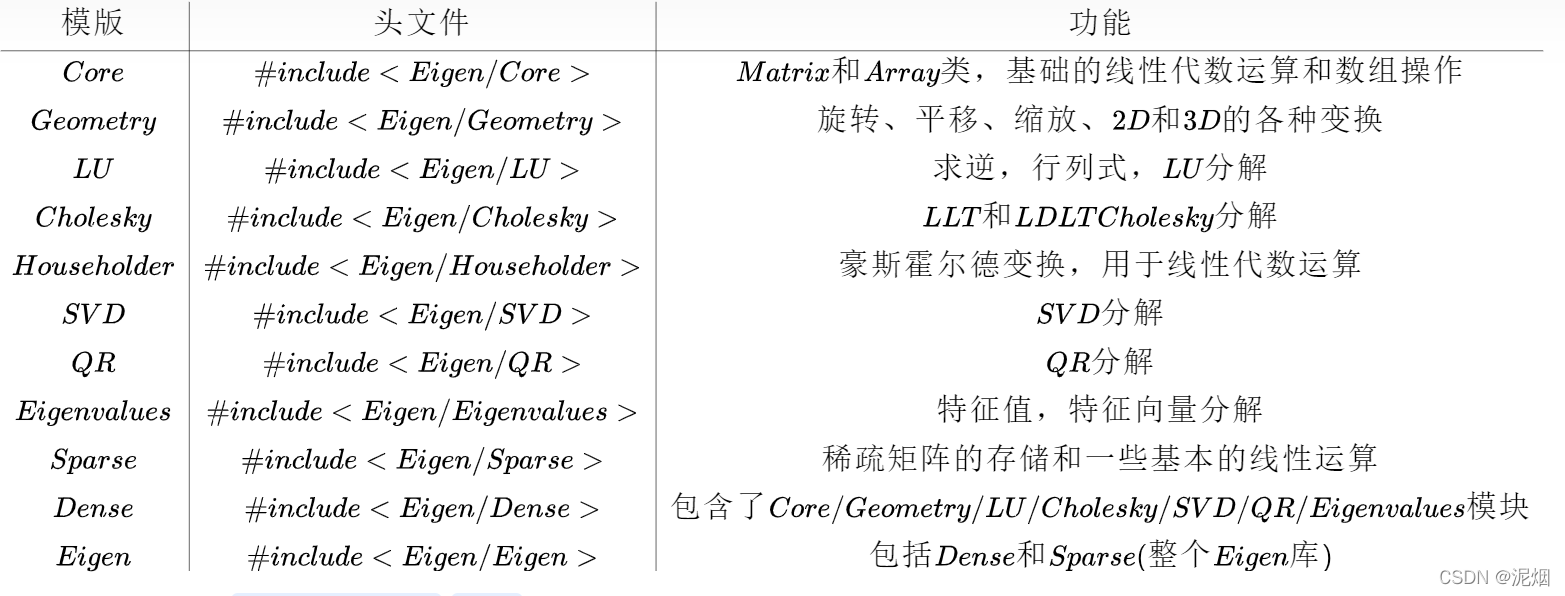
Eigen: Matrix and vector arithmetic

矩阵/向量的练习:

注:C++中 三角函数运算使用弧度制

#include <iostream>
#include <Eigen/Dense>
 
using namespace Eigen;
 
int main()
{
    std::cout << "Example of cpp :\n";
    float a = 1.0, b = 2.0;
    std::cout << a << std::endl;
    std::cout << a / b << std::endl;
    std::cout << std::sqrt(b) << std::endl;//√2
    std::cout << std::acos(-1) << std::endl;//arccos(-1)
    std::cout << std::sin(30.0 / 180.0 * acos(-1)) << std::endl;//sin(30°)
 
    Matrix2d a;
    a << 8, 2,
        2, 1;
    MatrixXd b(2, 2);
    b << 4, 1,
        1, 4;
    std::cout << "a =\n" << a << std::endl;
    std::cout << "b =\n" << b << std::endl;
    std::cout << "a + b =\n" << a + b << std::endl;
    std::cout << "a - b =\n" << a - b << std::endl;
    std::cout << "Do: a += b;" << std::endl;
    a += b;
    std::cout << "Now: a =\n" << a << std::endl;
 
    MatrixXf i(3,3), j(3,3);
    i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
    j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;
    std::cout << "i * j =\n" << i*j << std::endl;
 
    Vector3d v(1, 2, 3);
    Vector3d w(1, 2, 4);
    std::cout << "v =\n" << v << std::endl;
    std::cout << "w =\n" << w << std::endl;
    std::cout << "v - 2 * w =\n" << v - 2 * w << std::endl;
 
    MatrixXf c(2, 3); 
    c << 1, 2, 3, 4, 5, 6;
    std::cout << "Here is the initial matrix c:\n" << c << std::endl;
 
    c.transposeInPlace();
    std::cout << "and after being transposed:\n" << c << std::endl;
}

• 测试效果:

Example of cpp :
1
0.5
1.41421
3.14159
0.5
a =
8 2
2 1
b =
4 1
1 4
a + b =
12 3
3 5
a - b =
4 1
1 -3
Do: a += b;
Now: a =
12 3
3 5
i * j =
37 36 35
82 84 77
127 132 119
v =
1
2
3
w =
1
2
4
v - 2 * w =
-1
-2
-5
Here is the initial matrix c:
1 2 3
4 5 6
and after being transposed:
1 4
2 5
3 6