[Games101笔记]Lecture3-4

该笔记基于闫令琪大神的cs课程及课后作业总结而成

three-dimensional Euclidean space 三维欧氏空间

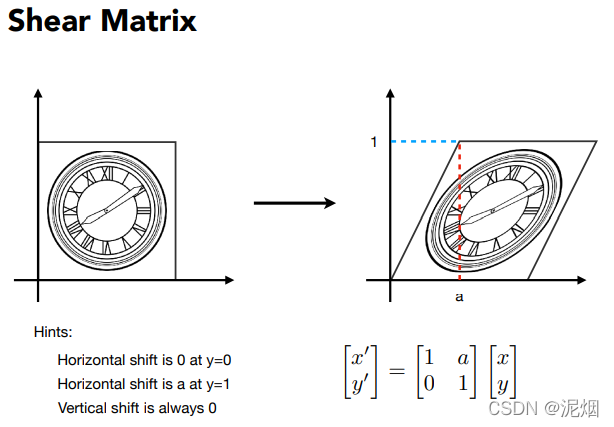
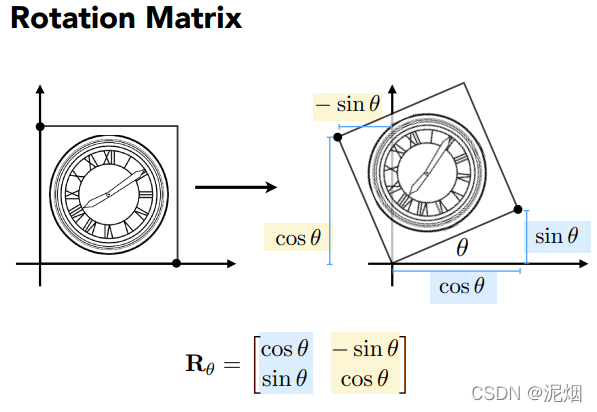
在伸缩,旋转后, 发现无法通过同维度的矩阵体现平移, 所以引入齐次方程

为了不把"平移变换"当做整个体系中的另类,再加一层向量,我的理解是补充常数(可以满足偏移等需求)

方便理解的阐释

仿射变换

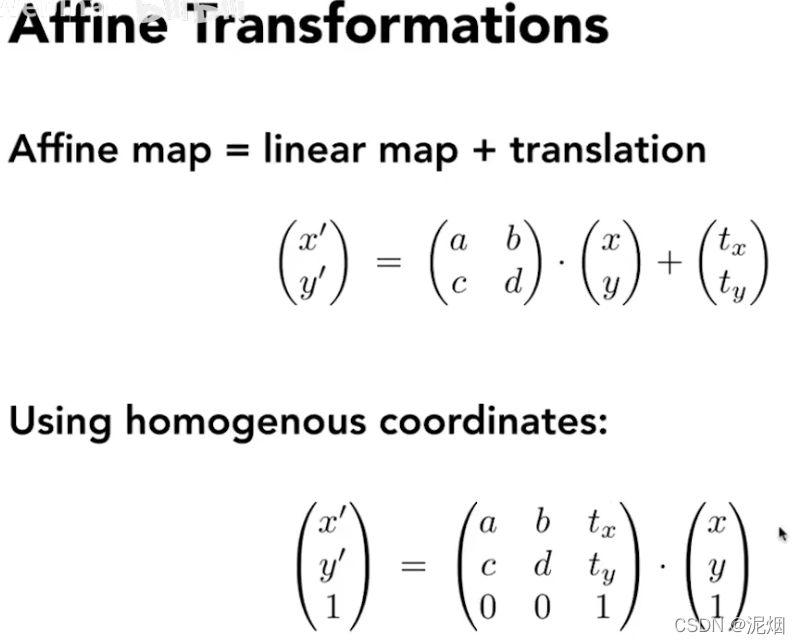
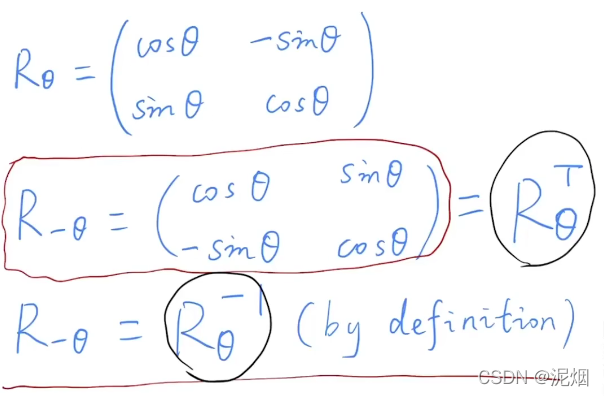
罗德里格斯旋转公式

推导

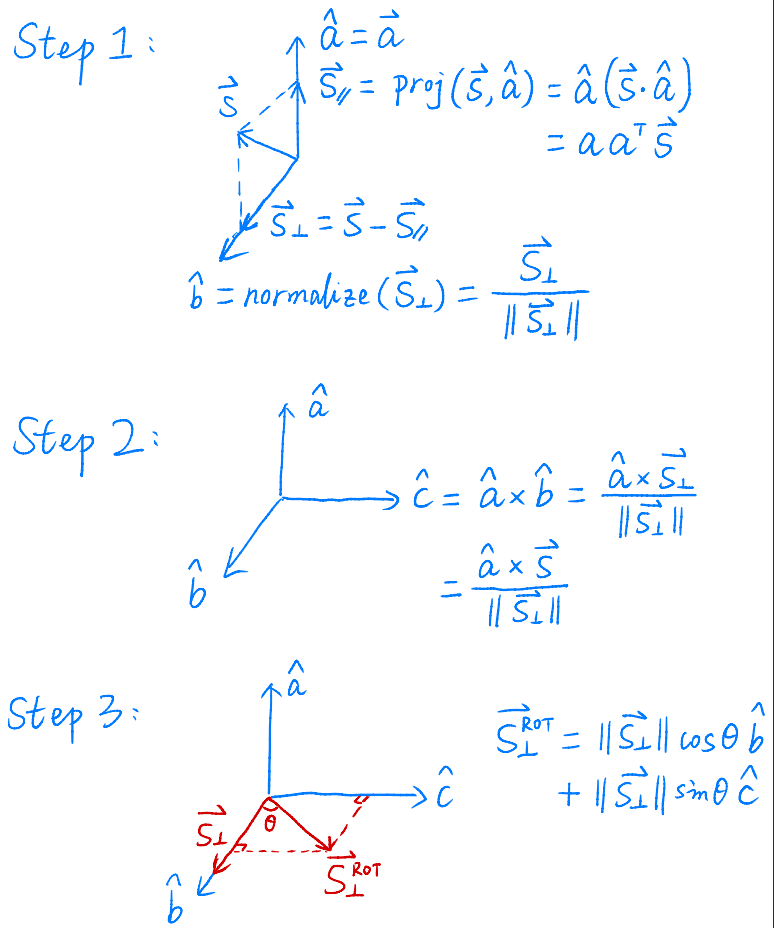
mvp变换

相机从一个坐标变换到世界坐标原点了，为了保持相机视图的图像不变，model也要跟着相机一起运动，相机变换到世界坐标的矩阵，就是model的变换矩阵，也就是MVP

先将当前物体的原点移至世界坐标原点T(view)

然后,为了求出当前整个参考系旋转至世界坐标系的变换R(view),可以先求其逆变换

旋转矩阵是正交矩阵 → 旋转矩阵的逆为它的转置,易得

正交投影

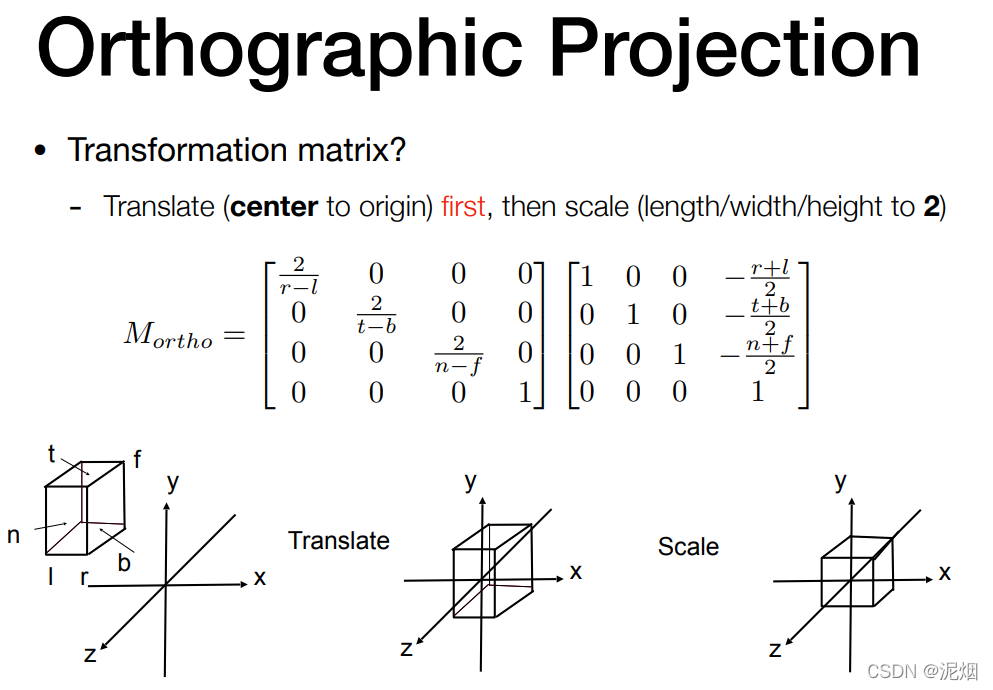
注意:

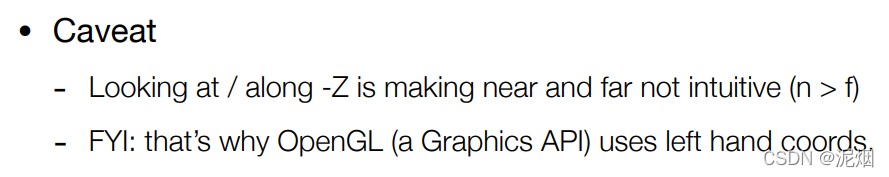
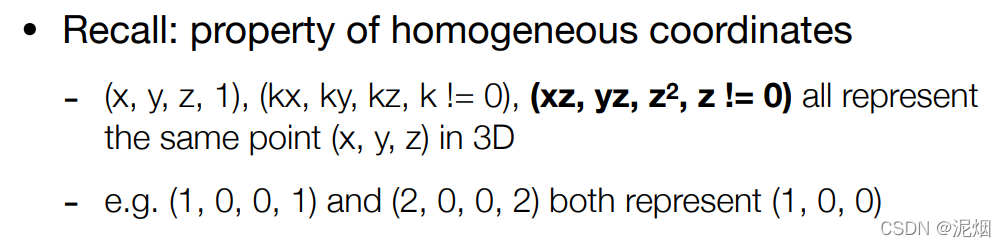
透射投影

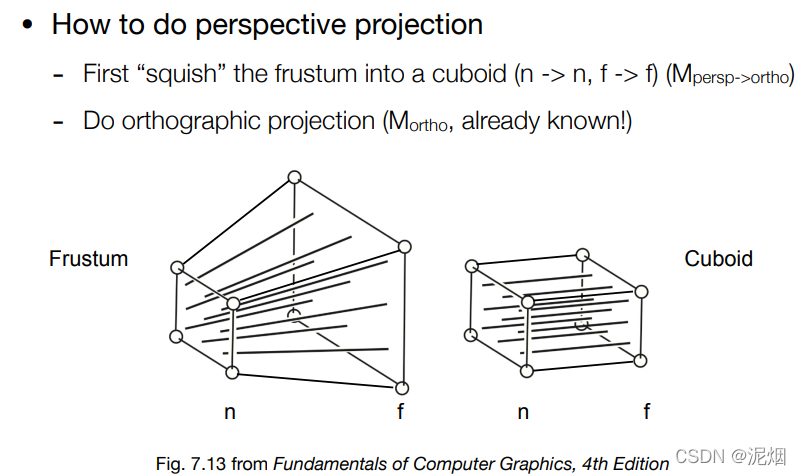
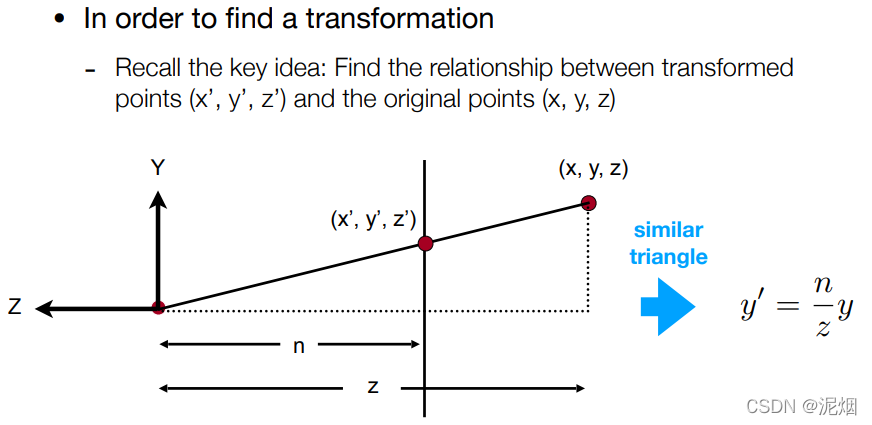
形象化的描述一下的话，就是利用这个变换矩阵将整个空间压缩了一下，使其对应了真正透视投影的坐标，最后不要忘了要利用正交转换到[-1, 1]^3的空间之内

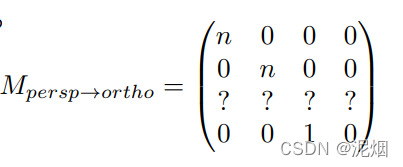
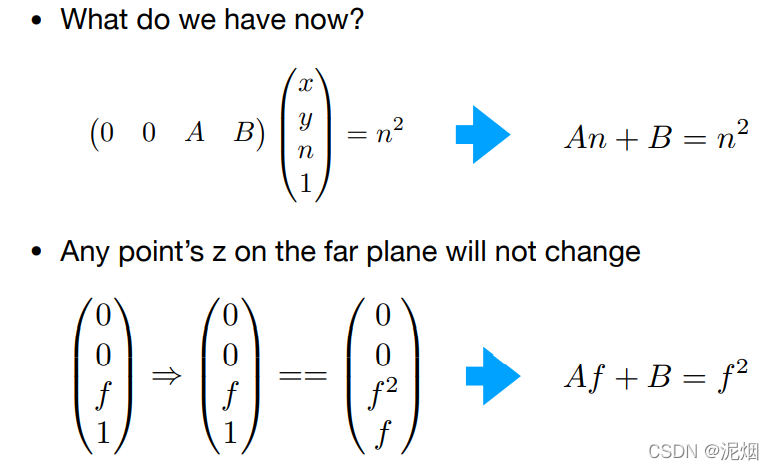
• 解得 A = n + f B = - f n

最后将这个被压缩过的空间，重新正交投影成标准小立方体，故定义透视投影变换

如下

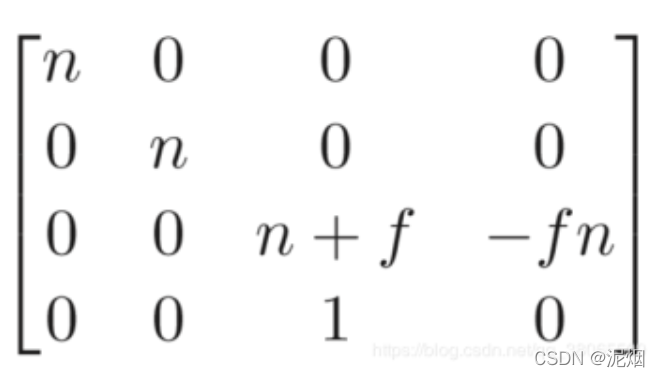
即

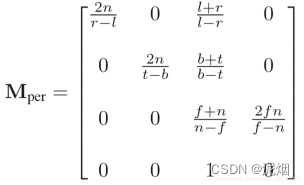
思考:
中间的经过透视投影, z值变得更小了