[Games101笔记] 作业1-2
作业1 基础版
//视图转换
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{
// 定义 4 * 4 的单位矩阵
Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
Eigen::Matrix4f translate;
// 初始化视角变换矩阵
translate << 1, 0, 0, -eye_pos[0],
0, 1, 0, -eye_pos[1],
0, 0, 1,-eye_pos[2],
0, 0, 0, 1;
view = translate * view;
return view;
}
透视投影变换矩阵
1 .将视锥压缩成正交投影变换矩阵可处理的形式
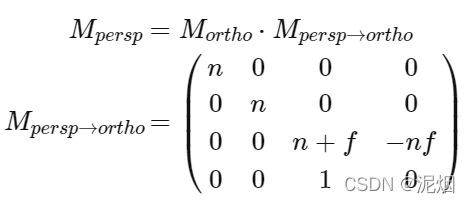
2 .正交投影
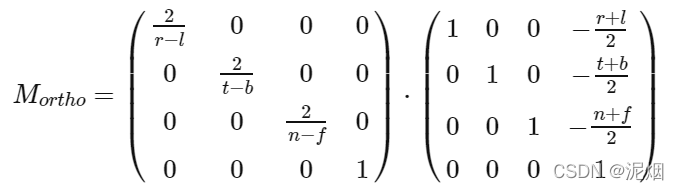
// 绕 z 轴旋转的变换矩阵
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
// 初始化一个单位矩阵model
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
// TODO: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
// ---------
Eigen::Matrix4f M_rotation;
// 弧度制
float rotation_radian = rotation_angle * MY_PI / 180;
// 绕z轴的旋转矩阵
M_rotation << cos(rotation_radian), -sin(rotation_radian), 0, 0,
sin(rotation_radian), cos(rotation_radian), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
model *= M_rotation;
// ---------
return model;
}
//eye_fov:纵向视野(度), aspect_ratio:宽高比
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// TODO: Implement this function
// Create the projection matrix for the given parameters.
// Then return it.
// ---------
Eigen::Matrix4f M_perToOrtho(4, 4);
Eigen::Matrix4f M_ortho_scale(4, 4);
Eigen::Matrix4f M_ortho_trans(4, 4);
// 纵向视野的一半,eye_fov * MY_PI / 2 / 180.0
float half_angle = eye_fov * MY_PI / 360.0;
float top = zNear * tan(half_angle);
float bottom = -top;
float right = top * aspect_ratio;
float left = -right;
M_ortho_trans << 1, 0, 0, -(right+left) / 2,
0, 1, 0, -(top+bottom) / 2,
0, 0, 1, -(zNear+zFar) / 2,
0, 0, 0, 1;
M_ortho_scale << 2 / (right-left), 0, 0, 0,
0, 2 / (top-bottom), 0, 0,
0, 0, 2 / (zNear-zFar), 0,
0, 0, 0, 1;
M_perToOrtho << zNear, 0, 0, 0,
0, zNear, 0, 0,
0 ,0, zNear+zFar, -zNear*zFar,
0, 0, 1, 0;
Eigen::Matrix4f M_ortho = M_ortho_scale * M_ortho_trans;
projection = M_ortho * M_perToOrtho;
// ---------
return projection;
}
效果
作业2
insideTriangle
//判断是否在三角形内
static bool insideTriangle(int x, int y, const Vector3f* _v)
{
// TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
std::vector<Vector3f> vecTriangle, vecInner;
vecTriangle.push_back({_v[1].x()-_v[0].x(), _v[1].y()-_v[0].y(), 0});
vecTriangle.push_back({_v[2].x()-_v[1].x(), _v[2].y()-_v[1].y(), 0});
vecTriangle.push_back({_v[0].x()-_v[2].x(), _v[0].y()-_v[2].y(), 0});
vecInner.push_back({x-_v[0].x(), y-_v[0].y(), 0});
vecInner.push_back({x-_v[1].x(), y-_v[1].y(), 0});
vecInner.push_back({x-_v[2].x(), y-_v[2].y(), 0});
int cntPosi = 0, cntNega = 0;
for(int i = 0; i < 3; i ++)
{
if(vecTriangle[i].cross(vecInner[i]).z() < 0)
cntNega ++;
else
cntPosi ++;
}
// 判断该点是否在三个向量同侧, 即内部
if(cntNega == 3 || cntPosi == 3) return true;
else return false;
}
rasterize_triangle
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// TODO : Find out the bounding box of current triangle.
//找bounding box的边界
int vertical_min, vertical_max, cross_min, cross_max;
vertical_min = v[0].y() < v[1].y() ? v[0].y() : v[1].y();
vertical_min = vertical_min < v[2].y() ? vertical_min : v[2].y();
vertical_max = v[0].y() > v[1].y() ? v[0].y() : v[1].y();
vertical_max = vertical_max > v[2].y() ? vertical_max : v[2].y();
cross_min = v[0].x() < v[1].x() ? v[0].x() : v[1].x();
cross_min = cross_min < v[2].x() ? cross_min : v[2].x();
cross_max = v[0].x() > v[1].x() ? v[0].x() : v[1].x();
cross_max = cross_max > v[2].x() ? cross_max : v[2].x();
// iterate through the pixel and find if the current pixel is inside the triangle
float alpha, beta, gamma;
for(float i = int(cross_min)-1; i <= int(cross_max)+1; i ++)
{
for(float j = int(vertical_min)-1; j <= int(vertical_max)+1; j ++)
{
// iterate through the pixel and find if the current pixel is inside the triangle
if(insideTriangle(i, j, t.v))
{
// If so, use the following code to get the interpolated z value.
std::tie(alpha, beta, gamma) = computeBarycentric2D(i+0.5, j+0.5, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
if(-z_interpolated < depth_buf[get_index(i, j)]){
set_pixel({i, j, 0}, t.getColor());
depth_buf[get_index(i, j)] = -z_interpolated;
}
}
}
}
}
效果
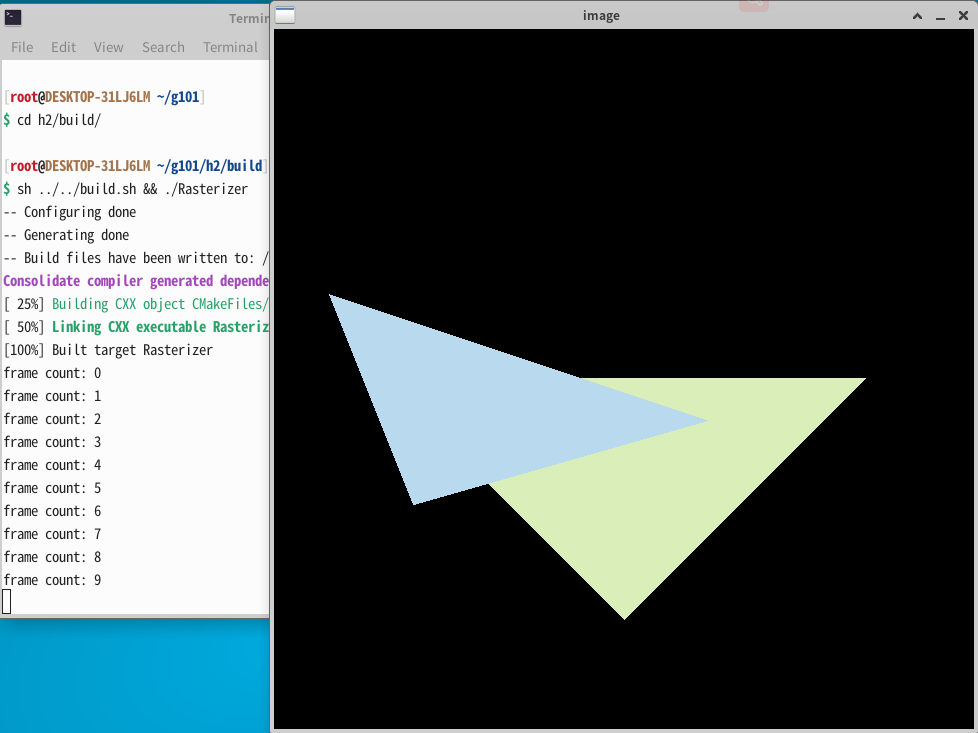
本文来自博客园,作者:泥烟,CSDN同名, 转载请注明原文链接:https://www.cnblogs.com/Knight02/articles/15798993.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号