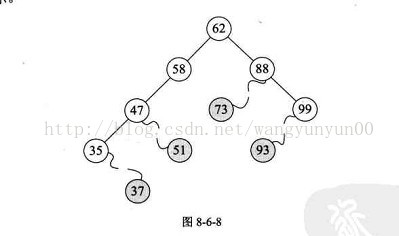
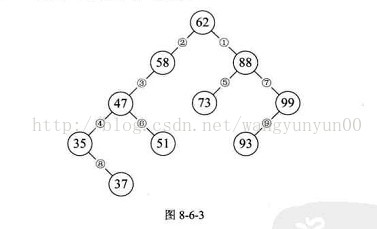
二叉排序树
二叉排序树,又称为二叉查找树。它或者是一颗空树,或者具有下列性质的二叉树。
-
若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
-
若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
-
它的左、右子树也分别为二叉排序树。
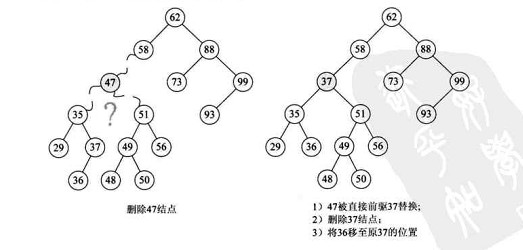
二叉排序树的难点在于删除操作
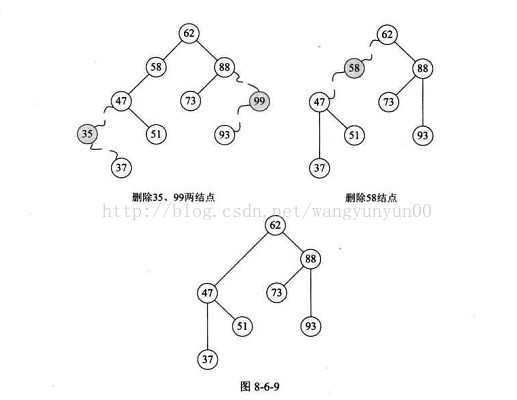
删除节点有三种情况分析:
a. 叶子节点;(直接删除即可)

b. 仅有左或右子树的节点;(上移子树即可)
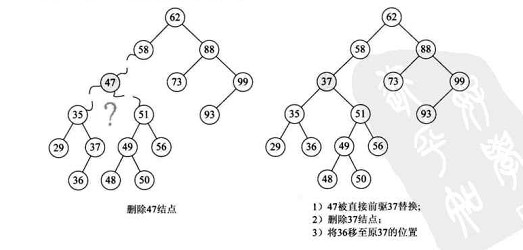
c. 左右子树都有的节点。( 用删除节点的直接前驱或者直接后继来替换当前节点,调整直接前驱或者直接后继的位置)
二叉排序树的基本操作:
1 #include<bits/stdc++.h>
2 using namespace std;
3
4 typedef struct tree{//二叉树节点结构定义
5 int date;
6 struct tree *lchild,*rchild;//定义左右子树
7 }Binode,*Bitree;
8
9 void insert(Bitree t,int date){//插入
10 Bitree p,s,fa;
11 p=t;
12 while(p){//查找date应在的位置
13 if(date<p->date){
14 fa=p;
15 p=p->lchild;
16 }
17 else if(date>p->date){
18 fa=p;
19 p=p->rchild;
20 }else{
21 cout<<"已存在"<<endl;
22 return ;
23 }
24 }//由于buildit为&t,此处fa和p的操作都直接作用于t上。
25 s=(Bitree)malloc(sizeof(Binode));//申请空间
26 s->date=date;
27 s->lchild=s->rchild=NULL;
28 if(s->date<fa->date){
29 fa->lchild=s;
30 cout<<"已插入"<<s->date<<endl;
31 }
32 else{
33 fa->rchild=s;
34 cout<<"已插入"<<s->date<<endl;
35 }
36 }
37
38 void Buildit(Bitree &t,int n){//构建二叉排序树
39 int date;
40 cin>>date;
41 t=(Bitree)malloc(sizeof(Binode));//申请空间
42 t->date=date;
43 t->lchild=t->rchild=NULL;//将左右子树设为NULL
44 for(int i=1;i<n;i++){//插如n次
45 cin>>date;
46 insert(t,date);
47 cout<<"创建完毕"<<endl;
48 }
49
50 }
51
52 int search1(Bitree t,int key){//搜索节点(非递归)
53 Bitree p;
54 p=t;
55 while(p){
56 if(key< p->date){
57 p=p->lchild;
58 }else if(key> p->date){
59 p=p->rchild;
60 }
61 else{
62 cout<<"已找到"<<p->date<<endl;
63 return 1;
64 }
65 }
66 return 0;
67 }
68
69 int search2(Bitree t,int key){//搜索节点(递归)
70 Bitree p;
71 p=t;
72 if(!t){
73 return 0;
74 }
75 if(p->date==key){
76 cout<<"已找到"<<p->date<<endl;
77 return 1;
78 }else if(p->date<key){
79 return search2(p->rchild,key);
80 }else{
81 return search2(p->lchild,key);
82 }
83 }
84
85 void Delete(Bitree t,int key){//删除节点
86 Bitree p,cur,par;
87 p=t;
88 while(p){//查找节点位置
89 if(key==p->date){
90 break;
91 }else if(key<p->date){
92 par=p;
93 p=p->lchild;
94 }else{
95 par=p;
96 p=p->rchild;
97 }
98 }
99 if(!p){
100 return ;
101 }
102 if(!p->lchild){//没有左子树
103 if(p==t){//根节点
104 t=p->rchild;
105 }else if(par->lchild==p){//par为p的父节点
106 par->lchild=p->rchild;
107 }else{
108 par->rchild=p->rchild;
109 }
110 }else{//有左子树
111 cur=p->lchild;
112 par=cur;
113 while(cur->rchild){
114 par=cur;
115 cur=cur->rchild;
116 }
117 if(par==p->lchild){//p的左孩子没有右子树
118 p->date=par->date;
119 p->lchild=par->lchild;
120 free(par);
121 }
122 else{//有右子树
123 p->date=cur->date;
124 par->rchild=cur->lchild;
125 free(cur);
126 }
127 }
128 }
129
130 void Inorder(Bitree t){
131 if(!t)
132 return ;
133 Inorder(t->lchild);
134 cout<<t->date<<" ";
135 Inorder(t->rchild);
136 }
137
138 int main(){
139 Bitree t;
140 int n,key,select;
141 while(1){
142 printf(" ------------------\n");
143 printf(" 1、建立二叉排序树\n");
144 printf(" 2、输出中序遍历结果\n");
145 printf(" 3、搜索数据\n");
146 printf(" 4、删除数据\n");
147 printf(" 5、插入数据\n");
148 printf(" 6、搜索数据(递归)\n");
149 printf(" ------------------\n");
150 cin>>select;
151 switch(select){
152 case 1:
153 cin>>n;
154 Buildit(t,n);
155 break;
156 case 2:
157 Inorder(t);
158 cout<<endl;
159 break;
160 case 3:
161 cin>>key;
162 search1(t,key);
163 break;
164 case 4:
165 cin>>key;
166 Delete(t,key);
167 break;
168 case 5:
169 cin>>key;
170 insert(t,key);
171 break;
172 case 6:
173 cin>>key;
174 search2(t,key);
175 break;
176 default:
177 return 0;
178 }
179 }
180 return 0;
181 }