Educational Codeforces Round 52 (Rated for Div. 2) Make It Equal

C. Make It Equal

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There is a toy building consisting of 𝑛n towers. Each tower consists of several cubes standing on each other. The 𝑖i-th tower consists of ℎ𝑖hicubes, so it has height ℎ𝑖hi.

Let's define operation slice on some height 𝐻H as following: for each tower 𝑖i, if its height is greater than 𝐻H, then remove some top cubes to make tower's height equal to 𝐻H. Cost of one "slice" equals to the total number of removed cubes from all towers.

Let's name slice as good one if its cost is lower or equal to 𝑘k (𝑘≥𝑛k≥n).

Calculate the minimum number of good slices you have to do to make all towers have the same height. Of course, it is always possible to make it so.

Input

The first line contains two integers 𝑛n and 𝑘k (1≤𝑛≤2⋅1051≤n≤2⋅105, 𝑛≤𝑘≤109n≤k≤109) — the number of towers and the restriction on slices, respectively.

The second line contains 𝑛n space separated integers ℎ1,ℎ2,…,ℎ𝑛h1,h2,…,hn (1≤ℎ𝑖≤2⋅1051≤hi≤2⋅105) — the initial heights of towers.

Output

Print one integer — the minimum number of good slices you have to do to make all towers have the same heigth.

Examples

input

Copy

5 5
3 1 2 2 4

output

Copy

2

input

Copy

4 5
2 3 4 5

output

Copy

2

Note

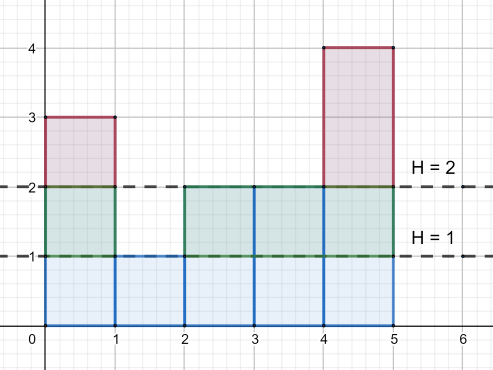
In the first example it's optimal to make 22 slices. The first slice is on height 22 (its cost is 33), and the second one is on height 11 (its cost is 44).

 

题意：

　　有上图所示的n个矩形，现在把他们切成一样高，只能平行于x轴切，每次所切的小矩形不能超过k个，求最少需要切多少刀。

分析：

　　暴力求每一层有多少个矩形，然后一层一层的切就可以了。关键在于怎么求出来每一层有多少个小矩形。

///  author:Kissheart  ///
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#include<queue>
#include<deque>
#include<ctype.h>
#include<map>
#include<set>
#include<stack>
#include<string>
#define INF 0x3f3f3f3f
#define FAST_IO ios::sync_with_stdio(false)
const double PI = acos(-1.0);
const double eps = 1e-6;
const int MAX=2e5+10;
const int mod=1e9+7;
typedef long long ll;
using namespace std;
#define gcd(a,b) __gcd(a,b)
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
inline ll qpow(ll a,ll b){ll r=1,t=a; while(b){if(b&1)r=(r*t)%mod;b>>=1;t=(t*t)%mod;}return r;}
inline ll inv1(ll b){return qpow(b,mod-2);}
inline ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll r=exgcd(b,a%b,y,x);y-=(a/b)*x;return r;}
inline ll read(){ll x=0,f=1;char c=getchar();for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;for(;isdigit(c);c=getchar()) x=x*10+c-'0';return x*f;}
//freopen( "in.txt" , "r" , stdin );
//freopen( "data.txt" , "w" , stdout );
ll n,k;
ll a[MAX],b[MAX],cur;
int cmp(ll x,ll y)
{
    return x>y;
}
int main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    sort(a+1,a+1+n,cmp);
    for(int i=1;i+1<=n && a[i]!=a[n];i++)
    {
        while(a[i]==a[i+1]) i++;                     ///8 8 4 4 3 2
        for(int j=1;j<=a[i]-a[i+1];j++)
            b[++cur]=i;
    }
    ll ans=0;
    /*for(int i=1;i<=cur;i++)
    {
        printf("%lld\n",b[i]);
    }*/

    for(int i=1;i<=cur;)
    {
        ll sum=0;
        while(sum+b[i]<=k && i<=cur)
            sum+=b[i++];
        ans++;
    }
    printf("%lld\n",ans);
    
    return 0;
}