模板 - 数学 - 组合数学 - 第二类斯特林数

组合意义

记 \(S(n,m)\) 表示，把 \(n\) 个不同的小球，放在 \(m\) 个相同的盒子里，且每个盒子至少有 \(1\) 个球，的方法数。

记 \(S(n,m)\) 表示，把 \(n\) 个不同的元素，划分为 \(m\) 个非空集合的方法数。

显然 \(S(0,0)=1\) ，而 \(S(n,0)\) 当 \(n\geq 1\) 时显然是不合法的方案， \(S(0,m)\) 当 \(m\geq 1\) 时因为至少有 \(1\) 个空盒子所以也显然是不合法的方案。

递推

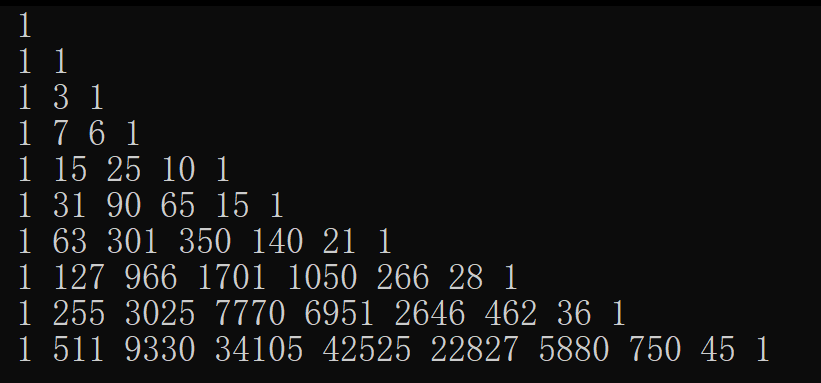
\(S(n,m)=S(n-1,m-1)+m*S(n-1,m)\)

含义是，多一个新的球，那么假如再新加一个盒子去装，显然是一种办法，否则要把这个球放在先前已有的 \(m\) 个盒子中的任意一个，由于新加的这个小球是全新的，所以这个和组合数的递推公式不一样。

使用递推去求解需要 \(O(nm)\)。

ll S[1005][1005];

void GetS(int n, int m) {
    memset(S, 0, sizeof(S));
    S[0][0] = 1;
    for(int i = 1; i <= n; ++i) {
        int cj = min(i, m);
        for(int j = 1; j <= cj; ++j)
            S[i][j] = (S[i - 1][j - 1] + 1ll * j * S[i - 1][j]) % MOD;
    }
    for(int i = 1; i <= n; ++i) {
        int cj = min(i, m);
        for(int j = 1; j <= cj; ++j)
            printf(" %lld", S[i][j]);
        puts("");
    }
    return;
}

通项

\(S(n,m)=\frac{1}{m!}(\sum\limits_{i=0}^{m}(-1)^i*C(m,i)*(m-i)^n)\)

使用通项去求解只需要 \(O(mlogn)\)。

ll qpow(ll x, int n) {
    ll res = 1;
    if(x >= MOD)
        x %= MOD;
    while(n) {
        if(n & 1) {
            res = res * x;
            if(res >= MOD)
                res %= MOD;
        }
        x = x * x;
        if(x >= MOD)
            x %= MOD;
        n >>= 1;
    }
    return res;
}

ll S(int n, int m) {
    ll sum = 0;
    sum += qpow(m, n);
    ll fac1 = 1, fac2 = 1;
    for(int i = 1; i <= m; ++i) {
        fac1 *= (m + 1 - i);
        if(fac1 >= MOD)
            fac1 %= MOD;
        fac2 *= i;
        if(fac2 >= MOD)
            fac2 %= MOD;
        ll tmp = (i & 1) ? (MOD - 1) : (1);
        tmp *= fac1;
        if(tmp >= MOD)
            tmp %= MOD;
        tmp *=  qpow(fac2, MOD - 2);
        if(tmp >= MOD)
            tmp %= MOD;
        tmp *=  qpow(m - i, n);
        if(tmp >= MOD)
            tmp %= MOD;
        sum += tmp;
        if(sum >= MOD)
            sum -= MOD;
    }
    sum *= qpow(fac1, MOD - 2);
    if(sum >= MOD)
        sum %= MOD;
    return sum;
}

卷积

使用卷积可以求出同一个 \(n\) 在不同的 \(m\) 取值下的所有的斯特林数。详见下面博客。

参考资料

https://www.cnblogs.com/clno1/p/10809678.html