Codeforces Round #633 (Div. 2)

题目链接：https://codeforces.com/contest/1339

A - Filling Diamonds

题解：直接输出n，注意到每个竖着的菱形都可以作为中心。

B - Sorted Adjacent Differences

题意：给一个数组，确定其一个顺序，使得相邻元素的差的绝对值非降序。

题解：容易看到每个元素只会影响其附近的两个元素，那么假如其附近的两个元素本身存在某种大小关系就很好办，理所当然的会想到下面的算法。

先排序，然后把前半部分翻转，再把前半部分和后半部分交叉。

int a[100005];

void TestCase() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    sort(a + 1, a + 1 + n);
    int m = n / 2;
    reverse(a + 1, a + 1 + m);
    int j1 = 1, j2 = m + 1;
    for(int i = 1; i <= n; ++i) {
        if(i & 1) {
            printf("%d%c", a[j2++], " \n"[i == n]);
            continue;
        } else {
            printf("%d%c", a[j1++], " \n"[i == n]);
            continue;
        }
    }
    return;
}

*C - Powered Addition

题意：给一个数组，第x秒可以给任意个数都同时加上2^(x-1)，求最少需要多少秒使得数组变成非降序。

题解：看起来就很贪心，线性的做法很好想，每次确定这个数字是不是比前一个小，若是，则把已经有的秒数添加一部分在这个数字上面，不足则扩充秒数，这样总是可以使得这个数字和前一个数字相等。但是刚好相等不见得是好的，取决于后一个数字有多大，假如后一个数字比这个数字大，那么还是应该把当前已有的秒数全部用完。

更好想的是二分。假如我二分枚举一个x（或者直接枚举x就行了，反正也就是31个），那么最后一个元素必定是越大越好，全部加上，前一个元素尽可能加到和后一个元素相等，若本身就比后一个元素大则无解。

ll a[100005];
ll b[100005];

void TestCase() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%lld", &a[i]);
    for(int x = 0; x <= 50; ++x) {
        ll maxdif = (1ll << x) - 1;
        int suc = 1;
        b[n] = a[n] + maxdif;
        for(int i = n - 1; i >= 1; --i) {
            if(a[i] > b[i + 1]) {
                suc = 0;
                break;
            } else
                b[i] = min(a[i] + maxdif, b[i + 1]);
        }
        if(suc) {
            printf("%d\n", x);
            return;
        }
    }
    exit(-1);
}

有了这个算法之后，貌似可以把枚举x的过程也给优化掉，但是真的麻烦。

官方题解说是直接正向扫一遍就行了，dp/贪心求出每个ai要去到哪个bi，易知答案就是最大的bi-ai的位数，容易看出bi就是前一个b{i-1}和ai之中的最大值。

ll a[100005];
ll b[100005];

void TestCase() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%lld", &a[i]);
    b[0] = -LINF;
    ll ans = 0;
    for(int i = 1; i <= n; ++i) {
        b[i] = max(b[i - 1], a[i]);
        ans = max(ans, b[i] - a[i]);
    }
    int x = 0;
    while(ans) {
        ans >>= 1;
        ++x;
    }
    printf("%d\n", x);
    return;
}

启发：这种题不见得会和秒数x有关，虽然枚举秒数x也是一种解法，但是可以多思考问题的本质。可以直觉观察出最优的序列b是唯一的，最优的序列b不仅用的秒数x是最小的，而且也是字典序最小的，每个a都去到其恰好需要去到的b。

*D - Edge Weight Assignment

昨晚好像想错了一点点。

题意：给一棵树，要求给每条边边赋一个可以无限大的正数权值，使得任意两个不同的叶子之间的简单路径的权值异或和为0，求有最少用多少种不同的权值和最多用多少种不同的权值。

题解：容易知道，连接在同一棵子树下的所有叶子对应的这些边都是权值相等的。不妨设这些边的权值都为1。若所有的两个叶子之间的距离都是偶数，那么全部都赋值为1就是一种结果，否则就存在一对叶子之间的距离是奇数（设为k），这样就要把中间的k-2条全部覆盖2，然后选两端有叶子的地方覆盖2，这样就有3种权值。也就是说最小答案不是1就是3。叶子之间的距离的奇偶性肯定是和叶子的深度的奇偶性有关的，随便定一个根节点，假如所有的叶子都是奇数深度或者所有的叶子都是偶数深度，答案就是1，否则就是3。

最大答案就更爽了，除了连接在同一棵子树下的所有叶子对应的这些边都是权值相等的以外，其他的是随便放的。构造的过程就是证明的过程，官方题解指出的是要从叶子开始构造，而不是从内部节点开始构造，构造的方法如下：

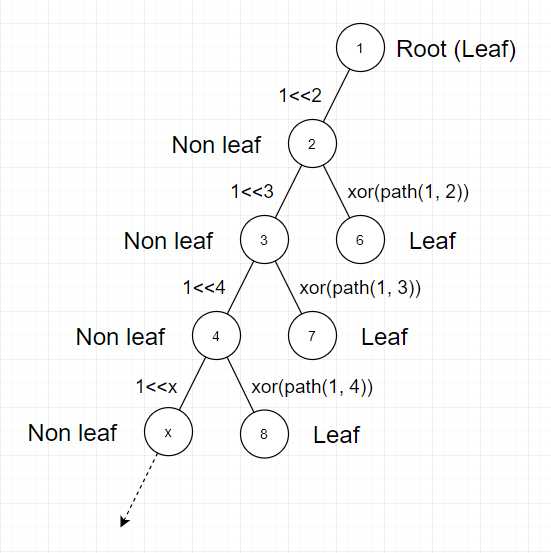
那么就是数一数有多少团叶子就可以了。