Codeforces Round #632 (Div. 2)

题目链接：https://codeforces.com/contest/1333

第二次打到2000以上，非常接近历史最高了。C题稍微演了一点，其他的看起来是正常发挥。

A - Little Artem

一个简单的构造，不需要搞棋盘格这么麻烦，直接全部染成同色然后把第一个格换掉，由于n和m都不少于2所以这个构造一定正确。

B - Kind Anton

一个简单的模拟，随便想想就可以了。

*C - Eugene and an array

+2了，太惨了，第一次是假算法+数组越界，第二次是假算法。

题意：给n个数的序列。定义一个连续区间是“好的”，当其不含有任何sum为0的连续子区间。求这个序列的所有连续子区间有哪些是“好的”。

题解：这种“sum为0”的好像见过很多次了，理所当然是用map<ll,int>保存最后一个sum为key的位置为value。不过有一点点细节，处理下面的数据：

7
1 2 -3 4 1 2 3

第4个数4，可以选择的范围是：[2,-3,4],[-3,4],[4]，要跳过上一步导致相等时已经跳过的1。然后可以非常容易发现，被跳过的数后面再也用不到（因为不可以包含这段sum为0的区间），所以能选择的位置被跳过的数和上一个sum相同的位置共同限制。

map<ll, int> MAP;
int a[2000005];
 
void TestCase() {
    MAP.clear();
    MAP[0] = 0;
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    ll sum = 0, ans = 0;
    int rightmost = 0;
    for(int i = 1; i <= n; ++i) {
        sum += a[i];
        if(MAP.count(sum))
            //printf("?\n");
            rightmost = max(rightmost, MAP[sum] + 1);
        ans += i - rightmost;
        MAP[sum] = i;
        //printf("i=%d ans=%lld\n", i, ans);
        //printf("  rightmost=%d\n", rightmost);
    }
    printf("%lld\n", ans);
    return;
}

*D - Challenges in school №41

题意：有一个n个箭头箭头序列，只能是左箭头或者右箭头，每次操作可以选一对相邻的相对的箭头变成相背的箭头。每秒操作至少1次，求能够恰好k秒把整个箭头序列变成没有任何相对的箭头。

如下图：

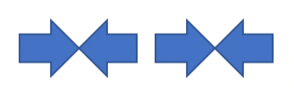
第1秒，选择两对相对的箭头同时翻转：

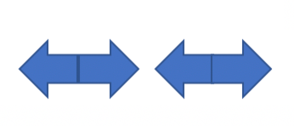
第2秒，选择唯一的相对的箭头翻转：

题解：n很小k很大，一开始以为要在某些步骤循环空耗箭头，但是手推了几个之后发现其实每个箭头要翻转多少次是已经确定好的。可以把左箭头理解为0，右箭头理解为1，这个就是一个冒泡排序，只不过每秒可以同时操作若干组互不影响的箭头。可以发现每个状态下都有一些位置是可以临位交换的，而且这些位置是可以同时发生变化互不影响的。假如每次都尽可能翻转所有的状态，那么必然是使用最少的时间来完成任务。显然可以把每次操作断成两段，这样就会+1s（太暴力了），那么非常显然有一个贪心算法：当剩余的操作数比剩余时间少时，每次尽可能翻转多的次数，直到某步之后剩余的操作数与剩余时间相等。

需要注意的是下面代码中推进j的时候，假如j被tmp截断，那么要重新计算j的位置。（还好输入了个比较大的数据，然后构造了一些k进行检查）。

char s[3005];
char t[3005];
vector<pair<int, int> > ans;
 
void TestCase() {
    int n, k;
    scanf("%d%d", &n, &k);
    scanf("%s", s + 1);
    //puts(s + 1);
    int suc = 0, Layer = 1;
    while(1) {
        //printf("Layer=%d\n", Layer);
        suc = 1;
        t[1] = s[1];
        for(int i = 2; i <= n; ++i) {
            if(s[i - 1] == 'R' && s[i] == 'L') {
                t[i - 1] = 'L';
                t[i] = 'R';
                ans.push_back({Layer, i - 1});
                suc = 0;
                //printf("swap %d\n", i - 1);
            } else
                t[i] = s[i];
        }
        if(suc) {
            --Layer;
            break;
        }
        for(int i = 1; i <= n; ++i)
            s[i] = t[i];
        //puts(s + 1);
        ++Layer;
    }
    //printf("Layer=%d\n", Layer);
    int m = ans.size();
    //printf("sumans=%d\n", m);
    if(m < k || k < Layer) {
        puts("-1");
        return;
    }
    int rest = m;
    int j = 0;
    while(rest > k) {
        --k;
        int cnt = 0;
        int begin_j = j;
        while(j < m && ans[j].first == ans[begin_j].first) {
            ++cnt;
            ++j;
        }
        int tmp = min(cnt, rest - k);
        printf("%d", tmp);
        j = begin_j;
        for(int k = 0; k < tmp; ++k)
            printf(" %d", ans[j++].second);
        printf("\n");
        //printf("rest k=%d\n", k);
        //printf("rest ans=%d\n", m - j);
        rest -= tmp;
    }
    assert(rest == k);
    while(rest--) {
        printf("1 %d", ans[j].second);
        ++j;
        printf("\n");
    }
    return;
}

一开始不知道会有多少次操作（然后聪明的直接换vector），现在明白了应该是不会超过n^2的量级，因为这个实际上是冒泡排序，操作次数和逆序数相同。

注意在翻转序列的时候要么像上面那样拷贝一串t（记得拷贝t[1]），要么在翻转之后多一次++i操作。

*E - Road to 1600

题意：构造一个n*n的棋盘，上面写着数字[1,n*n]，然后有一个“车”一个“后”，棋子都遵循下面的规则移动：

1. 若1步移动可达的格子中有未遍历的，则选择未遍历的格子中数字最小的格子移动。
2. 否则，若若1步移动可达的格子全部被遍历过，若还有未遍历的格子，则选择未遍历的格子中数字最小的格子传送。
3. 否则，停止算法。

棋子一开始在1号格，并且视作已经遍历了1号格。

构造的棋盘要使得“车”的传送次数严格小于“后”的传送次数。

题解：这种构造一般满足某种规律，n=1和n=2显然无解（“后”不可能需要传送）。

然后样例给了n=4的情况：

4 3 6 12 
7 5 9 15 
14 1 11 10 
13 8 16 2 

发现这个像什么？最后的三个数字是类似“马”移动的格子，启发一种构造思路：使得最后的几个数字发生传送，也就是诱导“后”去到一个陷阱里面，最后传送到目的地，“车”不需要传送。而且前面要安排一些斜对角的数字把“后”骗走。

参考资料：https://www.cnblogs.com/MZRONG/p/12674854.html

原来是要利用样例的结果，然后前面让“车”和“后”的走法完全相同，然后再一起走进样例里面。需要注意n=3也是存在的，注意到后是不能走“马”步的，通过奇妙的构造使得8在角落而9在“马”步的位置。

*F - Kate and imperfection

题意：给[1,n]的连续自然数。对[2,n]的每个k，都枚举所有大小恰好为k的子集，然后定义一个函数F，F参数是一个集合，其遍历集合中所有的二元组，求出二元组的gcd，然后取这些gcd里面的最大值，对每个k求函数F的最小值。

题解：每个数除掉最小质因数之后排序。容易发现这个构造确实是对的，首先质数除掉本身之后只剩下1，优先排他们。然后立刻排一个4，因为不可能再有gcd为1的选项了，加入一个4使得gcd为2是比较好的。这时不应该再插入8，因为插入8会需要把4删除。同理假如插入10，则要把5删除。这时要插入6，因为gcd为2的已经用完了，下一个应该插入的是9而不是8。假如当时多写几个样例可能会观察出一点规律吧，当时写了个12的情况：

1 2 3 5 7 11 4 6 9 8 10 12

其实当时已经发现了，是先摆所有的质数，然后摆只用2的，然后摆只用2和3的，但是这个8就没观察出规律，所以启发我不是每次都要把所有质数幂的数都一次处理掉，也不是考虑每个数是不是使用了其他质因数，有时可以从最小质因数的角度考虑。

比赛的时候还去找了莫比乌斯反演的模板，想要预处理 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^n[gcd(i,j)==k]\) 的值，但是忽略了一个事实就是题目要选的是子集而不能选择性忽视一些元素之间的gcd。

其实这个过程就是依次构造gcd=1，gcd=2，gcd=3，gcd=4的过程，但是推到gcd=4的时候我产生了怀疑。

const int MAXN = 5e5;
int p[MAXN + 5], ptop;
int pm[MAXN + 5];

void sieve() {
    int n = MAXN;
    pm[1] = 1;
    for(int i = 2; i <= n; ++i) {
        if(!pm[i]) {
            p[++ptop] = i;
            pm[i] = i;
        }
        for(int j = 1; j <= ptop; ++j) {
            int t = i * p[j];
            if(t > n)
                break;
            pm[t] = p[j];
            if(i % p[j])
                ;
            else
                break;
        }
    }
}

void TestCase() {
    sieve();
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        pm[i] = i / pm[i];
    sort(pm + 1, pm + 1 + n);
    for(int i = 2; i <= n; ++i)
        printf("%d%c", pm[i], " \n"[i == n]);
    return;
}